5. Массообменные процессы

5.1. Классификация и краткая характеристика процессов массообмена.

Массообмен – это процесс, при котором одно или несколько веществ переходит из одной фазы в другую.

Наиболее широко в пищевой промышленности применяются следующие массообменные процессы:

Сушка – удаление влаги из материалов путем ее испарения. Влага при этом переходит из влажных материалов в газовую или паровую фазу.

Экстрагирование – извлечение из твердого или жидкого сложного по составу вещества одного или нескольких компонентов с помощью растворителя, обладающего избирательной растворимостью. Вещество в этом случае переходит из твердой фазы в жидкую или из жидкой в жидкую.

Кристаллизация – Возникновение и рост кристаллов – представляет собой переход из жидкой (газообразной) фазы в твердую.

Адсорбция – избирательное поглощение газов, паров или растворимых в жидкости веществ в результате их концентрирования на поверхности раздела фаз или в объеме пор твердого тела. Связана с переходом вещества из газообразной (жидкой) фазы в твердую. Обратный процесс – десорбция – используется для регенерации поглощенного вещества из поглотителя.

Абсорбция – поглощение газа жидкостью, т.е. процесс разделения, характеризуемый переходом вещества из газовой фазы в жидкую.

Перегонка – однократное частичное испарение жидкой смеси и конденсация образующихся паров, ректификация – многократное частичное испарение жидкой смеси и конденсация образующихся паров с целью разделения компонентов, входящих в жидкую смесь. В этих процессах имеет место переход вещества из жидкой фазы в паровую и из паровой в жидкую.

Во всех перечисленных выше процессах вещества, которыми обмениваются фазы, должны переместиться внутри одной из фаз к поверхности раздела фаз, пересечь поверхности раздела и удалиться от поверхности раздела внутрь другой фазы. Совокупность перечисленных трех стадий процесса массообмена между фазами обычно называют массопередачей.

Перенос вещества (массы) внутри каждой из фаз может осуществляться двумя способами: молекулярной диффузией и конвективным переносом.

Первый из них связан с тепловым движением структурных частиц (атомов, молекул и др.), второй – с перемещением “молярных” объемов среды, т.е. объемов среды, состоящих из большого числа элементарных (структурных) частиц вещества.

Все массообменные процессы обладают ряжом общих признаков:

1. Они применяются для разделения смесей.

2. В любом процессе участвуют по крайней мере две фазы: жидкая и паровая, жидкая и газовая, твердая и жидкая и т.д.

3. Переход вещества из одной фазы в другую осуществляется за счет диффузии.

4. Движущей силой массообменных процессов является разность концентраций или градиент концентраций. Процесс протекает в направлении той фазы, в которой концентрация компонента меньше.

5. Перенос вещества из одной фазы в другую происходит через границу раздела фаз, на которой предполагается состояние равновесия фаз.

6. Диффузионные процессы обратимы, т.е. направление процесса определяется законами фазового равновесия фактическими концентрациями компонентов в обеих фазах и внешними условиями (температура, давление). Так, например, при повышении температуры и понижении давления поглощение газа жидкостью (абсорбция) может перейти в обратный процесс – удаление газа из жидкости (десорбция).

7. Переход вещества из одной фазы в другую заканчивается при достижении динамического равновесия. При этом обмен молекулами через границу раздела фаз не прекращается, однако концентрации компонентов в обеих фазах остаются неизменными и равными равновесными.

5.1.1. Массообмен между фазами. Молекулярная диффузия.

Рассмотрим основные закономерности, которые определяют передачу вещества из одной фазы в другую.

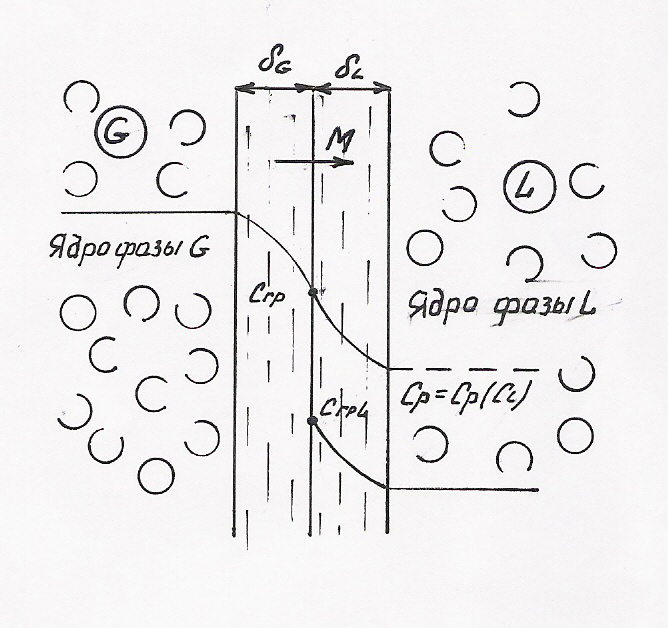
Пусть в фазе G концентрация рассматриваемого компонента больше концентрации того же компонента в фазе L, т.е. данный компонент переходит из фазы G в фазу L. Скорость переноса вещества равна М. Интересующий нас компонент должен быть доставлен к границе раздела фаз, чтобы мог произойти процесс массообмена между фазами.

Перенос вещества к границе раздела фаз осуществляется как путем молекулярной диффузии, так и путем конвективной диффузии.

В каждой фазе различают ядро потока данной фазы, в которой перенос вещества осуществляется преимущественно за счет конвективной диффузии, и пограничные слои толщиной расположенные у границы раздела фаз. В этих пограничных слоях массообменное происходит в основном за счет молекулярной диффузии. Толщина пограничных слоев зависит в первую очередь от скоростей движения взаимодействующих фаз, т.е. от гидродинамического режима в каждой фазе. Поскольку перенос вещества в пограничном слое происходит медленнее, чем в ядре потока, считают, что основное сопротивление переходу вещества из фазы в фазу сосредоточено в пограничном слое.

На границе раздела фаз предполагается равновесие между фазами, определяющее граничные концентрации yгр со стороны фазы G и хгр со стороны фазы L.

Молекулярная диффузия обусловлена переносом молекул вещества из области с большей его концентрацией и протекает в неподвижной среде или ламинарных пограничных слоях. Перенос вещества при молекулярной диффузии определяется законом Фика, который формируется следующим образом. Количество вещества dM, диффундирующего через слой в единицу времени, пропорционально площади слоя dF, перпендикулярной направлению диффузионного потока, и градиенту концентраций в направлении диффузии dc/dn, т.е.

dM = -D(dc/dn)dF

Знак минус указывает на то, что диффузия вещества идет в направлении уменьшения концентрации.

Движущийся слой процесса молекулярной диффузии является градиент концентраций dc/dn , который в общем случае изменяется в направлении переноса вещества. Средний градиент концентраций в первом приближении равен:

(dc/dn)ср =

Где - изменение концентраций компонента по толщине слоя;

- толщина слоя.

Коэффициент пропорциональности D, характеризующий скорость диффузии, называют коэффициентом диффузии. Он показывает сколько вещества проходит через единицу поверхности в единицу времени при градиенте концентраций, равном единице.

В системе Си единицей измерения коэффициента диффузии будет м /с.

Коэффициент диффузии характеризует природную способность одного вещества проникать в среду другого. Коэффициент диффузии зависит от свойств диффундирующего компонента и фазы, в которой он диффундирует, а также температуры и давления (для газов). Числовые значения D определяют экспериментально; они приведены в справочниках.

5.1.2. Дифференциальное уравнение молекулярной и конвективной

диффузии.

Выделим в среде параллепипед с ребрами длиной dx, dy, и dz и рассмотрим потоки вещества в пределах одного объема. Если объемная концентрация на входе в выделенный элемент равна С, то перенос вещества будет происходить за счет наличия градиента концентраций вдоль соответствующих осей координат.

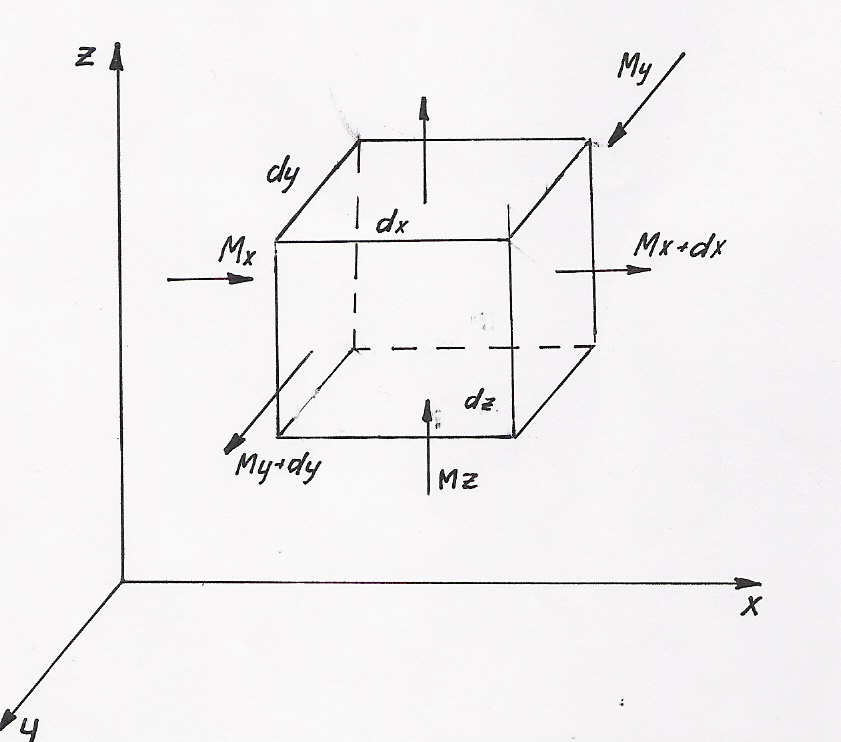
Рассмотрим перенос вещества в направлении оси Х.

Через левую грань параллепипеда, площадью dy*dz в единицу времени, входит масса вещества Мх, которая, согласно закону Фика равна:

Мх = -D( c/ x)dy*dz

Одновременно через правую грань уходит масса вещества Мх+dx, которая определяется следующим образом:

Mx+dx = -D

Разность приходной и расходной статей даст приращение вещества за счет молекулярной диффузии в направлении оси х.

dMx = Mx-Mx+dx = D

Аналогично для диффузии вещества в направлении других ослей получим следующее выражение в направлении оси у.

dMy = My – My+dy = D

В направлении оси z

dMz = Mz – Mz+dz = D

Общее приращение вещества в выделенном объеме будет равно:

dM = dMx+dMy+dMz = D (1)

C другой стороны, это же накопление вещества в системе может быть выражено через изменение концентраций во времени:

dM = (2)

Из сопоставления уравнений (1) и (2) получаем следующее уравнение молекулярной диффузии для нестационарного процесса:

=D (3)

Если процесс стационарный, т.е. концентрации во времени не изменяются, то и уравнение (3) примет вид:

(4)

Уравнение молекулярной и конвективной диффузии для нестационарного процесса будет иметь следующий вид:

(5)

Полученные дифференциальные уравнения молекулярной и конвективной диффузии не решаются аналитически в общем виде. Однако они могут быть использованы для получения безразмерных критериев подобия, применение которых при обработке экспериментальных данных по массообмену позволяет получать достаточно простые расчетные уравнения.

При практических расчетах применяют закон конвективной диффузии в следующем виде:

dM= (6)

где - коэффициент массоотдачи;

= с-с - движущая сила между ядром потока и на границе раздела

фаз.

Коэффициент массоотдачи представляет собои массу вещества, прошедшую через единицу поверхности в единицу времени при разности концентраций в ядре потока и на границе, равной единице.

Коэффициент массоотдачи характеризует скорость переноса массы в пределах одной фазы; его величина зависит от гидродинамических и физико -химических факторов, а также типа и размеров аппарата.

5.1.4. Подобие в процессах массообмена

Критерии подобия могут быть получены, например, при приведении дифференциального уравнения к безразмерному виду. При этом следует руководствоваться правилом, в соответствии с которым размерность дифференциала n-го порядка совпадает с размерностью самой переменной, а произведение n дифференциалов первого порядка имеет размерность переменной в n-ой степени, т.е.

[d x]=[x]и[ ]=[ ] (1)

Рассмотрим перенос вещества из ядра потока к границе раздела фаз. Тогда согласно закону Фика, к границе раздела фаз за счет молекулярной диффузии поступит следующее количество вещества в единицу времени:

dM=-D dF

То же количество вещества будет передано к границе раздела фаз, согласно закону конвективной диффузии:

dM= dF

Приравнивая правые части этих уравнений, получим:

-D

Разделив правую часть уравнения на левую и приняв во внимание соотношения (1), получим диффузионный критерий – критерий Нуссельта выражающий отношение характерного геометрического размера к толщине диффузионного пограничного подслоя.

(2)

где l – характерный линейный размер.

Для получения других критериев воспользуемся уравнением конвективной диффузии для одномерного потока массы в направлении оси Х, перпендикулярной поверхности контакта фаз:

(3)

Член отражает изменение концентраций во времени, т.е. неустановившийся характер процесса, член wx характеризует распределение концентрации, обусловленное конвективным переносом, и член - распределение концентрации за счет молекулярной диффузии.

Заменим члены уравнения (3) следующими величинами:

; wx ;

Разделим первый член левой части уравнения на его правую часть, получим:

безразмерный комплекс величин, который носит название диффузионного критерия Фурье.

Для того, чтобы устранить неудобство, связанное с применением в расчетах больших численных значений, этот критерий выражают комплексом величин, обратных полученному выше

характеризует постоянство отношения изменения концентрации во времени к изменению концентрации вследствие чисто молекулярного переноса.

Отношение второго слагаемого левой части уравнения (3) к его правой части представляет собой безразмерный комплекс величин, известных под названием диффузионного критерия Пекле

выражает меру отношения массы вещества, перемещаемой путем конвективного переноса и молекулярной диффузии, в сходственных точках подобных систем.

Во многих случаях вместо критерия Пекле используют отношение критериев Пекле и Рейнольдса, которое представляет собой диффузионный критерий Прандтля:

отражает физические свойства потока.

Гидродинамическое подобие в системах, где основное влияние оказывает сила тяжести, характеризуется критерием Фруда:

отражает влияние сил тяжести или собственного веса, на движение жидкости.

5.1.6. Основное уравнение массопередачи

Для расчета размеров аппарата, в котором должен осуществляться данный процесс массопередачи, необходимо знать скорость этого процесса.

Скорость процесса массопередачи равна массе вещества, переданного через единицу поверхности в единицу времени.

С другой стороны, скорость массообменного процесса пропорциональна движущей силе процесса. Следовательно можно записать:

или (1)

Величина К называется коэффициентом массопередачи; он характеризует массу вещества, переданную из фазы в фазу через единицу поверхности в единицу времени при движущей силе, равной единице, и отражает уровень интенсификации процесса: чем больше величина К, тем меньших размеров требуется аппарат для передачи заданного количества вещества.

Поскольку обычно движущая сила изменяется в ходе процесса массопередачи, пользуются усредненными величинами К и . Тогда основное уравнение массопередачи в интегральной форме имеет вид:

(2)

Движущая сила процесса массообмена может быть выражена разностью концентраций в той или другой фазе. Поэтому уравнение массопередачи (2) может быть записано в следующем виде:

Где х, у – рабочая концентрация в ядре потока соответствующей фазы;

хр, ур – равновесные концентрации в данной фазе, соответствующие

концентрациям распределяемого вещества в основной массе

(ядре) другой фазы.

Очевидно, что

или

отношение разности концентраций определяет средний тангенс угла наклона линии равновесия в рассматриваемом диапазоне изменения концентраций, т.е. коэффициенты массопередачи К и К однозначно взаимосвязаны через соответствующие движущие силы.

5.1.7. Определение коэффициента массопередачи через коэффициенты

массоотдачи.

Рассмотрим процесс массопередачи из фазы G в фазу L.

Перенос массы dM вещества из фазы G к границе раздела фаз в единицу времени будет определяться согласно уравнению конвективной диффузии:

(1)

uде - коэффициент массоотдачи.

Соответственно тоже количество вещества будет передано от границы раздела фаз в фазу L, т.е.

(2)

Кроме того, согласно основному уравнению массопередачи, можем записать, что

(3)

где - коэффициент массопередачи.

Пусть состояние равновесия, в том числе и на границе раздела фаз, будет описываться уравнением:

(4)

В общем случае и могут быть некоторыми функциями концентраций. При =0, отождествляется с константой равновесия. Тогда из уравнения линии равновесия следует, что

и (5)

Из уравнений (1), (2), (3) выразим разности концентраций через остальные переменные:

(6)

Приняв во внимание уравнение равновесия (5), второе уравнение системы (6) запишем в виде:

(7)

Сложив левые и правые части первого уравнения системы (6) и уравнения (7), получим:

(8)

Сопоставляя между собой третье уравнение системы (6) и уравнение (8) приходим к следующему соотношению:

(9)

Если основное уравнение массопередачи записать в виде

(10)

то путем аналогичных преобразований получим следующее выражение:

(11)

Из уравнений (9) и (11) следует, что

(12)

Каждый из членов правой части уравнений (9) и (11) выражает диффузионное сопротивление одной из фаз. Если одно из диффузионных сопротивлений весьма мало по сравнению с другим, то им можно пренебречь.

Уравнения (9) (11) позволяют определить величины коэффициентов массопередачи и , располагая коэффициентами массоотдачи и , которые могут быть определены экспериментально для опытных систем, моделирующих сопротивление массопереносу преимущественно только в одной фазе.

Если равновесная зависимость криволинейна, то для нахождения коэффициентов массопередачи и по двум коэффициентам массоотдачи процесс разбивают на отдельные участки, в пределах каждого из которых считают величиной постоянной. В этом случае коэффициент массопередачи будет изменяться по длине аппарата (зависеть от концентраций).

5.1.6. Материальный баланс массообменного процесса

Взаимодействие фаз в пределах всего аппарата или его отдельных участков контактных устройств может осуществляться по трем основным схемам: в противотоке, прямотоке и в перекрестном токе. От схемы движения потоков зависят пределы изменения концентраций в аппарате.

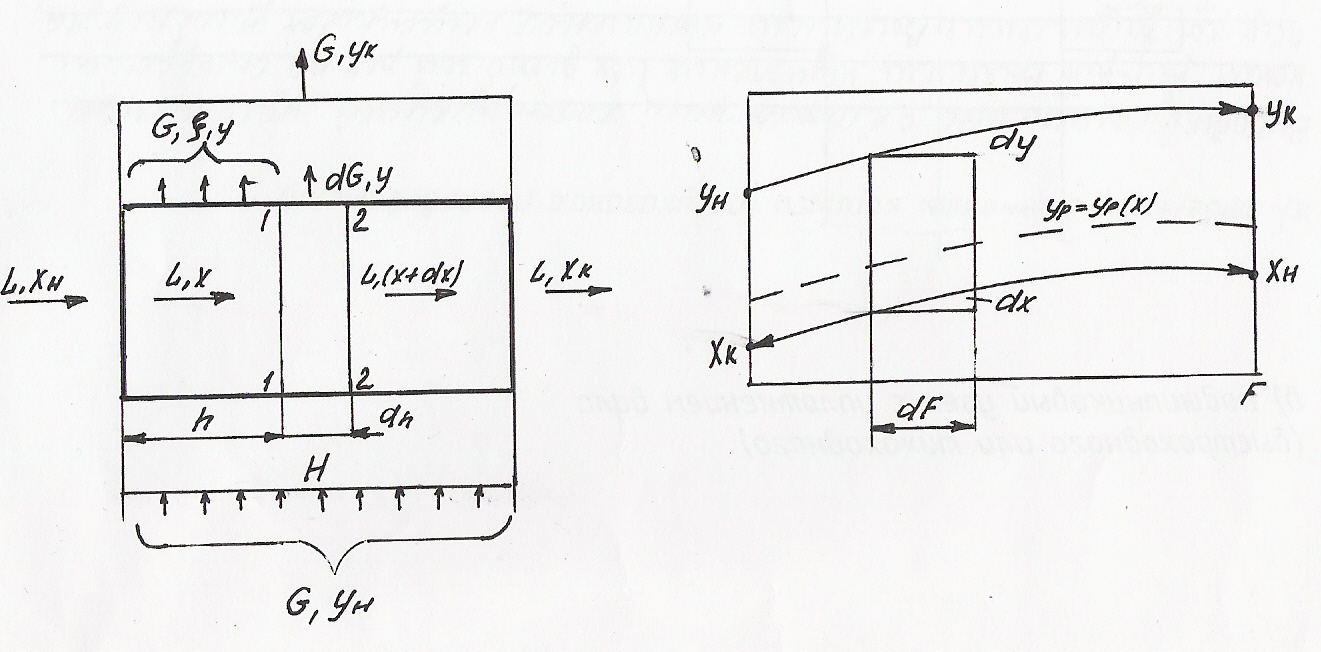
Пусть через массообменный аппарат движутся противотоком потоки двух фаз.

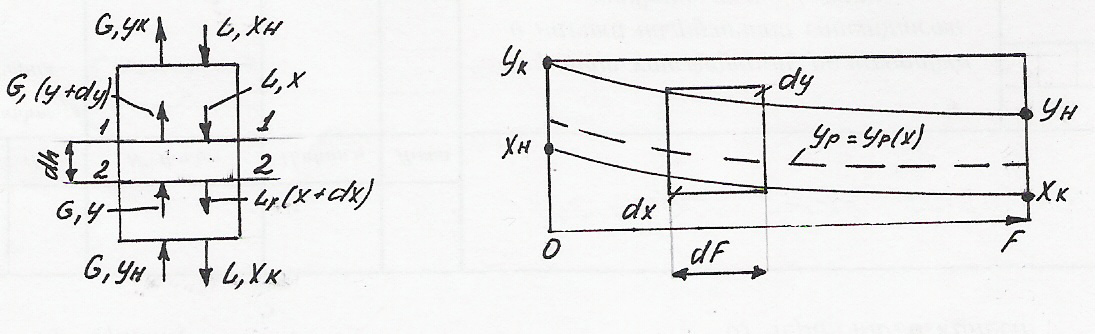
схема потоков изменение концентраций вдоль поверхности

контакта фаз

Секундный расход одной фазы (например, газа или пара), движущийся снизу вверх, составляет G, а другой фазы (например жидкости), движущейся сверху вниз, L. Концентрации компонентов в контактирующих фазах обозначим соответственно через y и х. В результате массообмена концентрации рассматриваемых компонентов изменяются от начальной до конечной величины.

Общий материальный баланс по данному компоненту для всего аппарата записывается так:

Следовательно, количество переданной массы М можно выразить следующим образом:

Отсюда соотношение между потоками контактирующих фаз равно:

(1)

При заданных концентрациях это выражение может быть использовано для определения величины i, а при заданной величине i – для расчета одной из конечных концентраций,

Для определения составов внутренних потоков составим уравнение материального баланса для части аппарата, расположенной ниже сечения 1-1

после преобразований получим так называемое уравнение рабочей линии

(2)

Уравнение рабочей линии дает зависимость между рабочими (неравновесными) составами фаз в произвольном сечении аппарата. Оно позволяет выявить изменение концентраций компонента по высоте аппарата.

В координатах х-у уравнение рабочей линии становится уравнением прямой, когда тангенс угла ее наклона к оси абсцисс равен

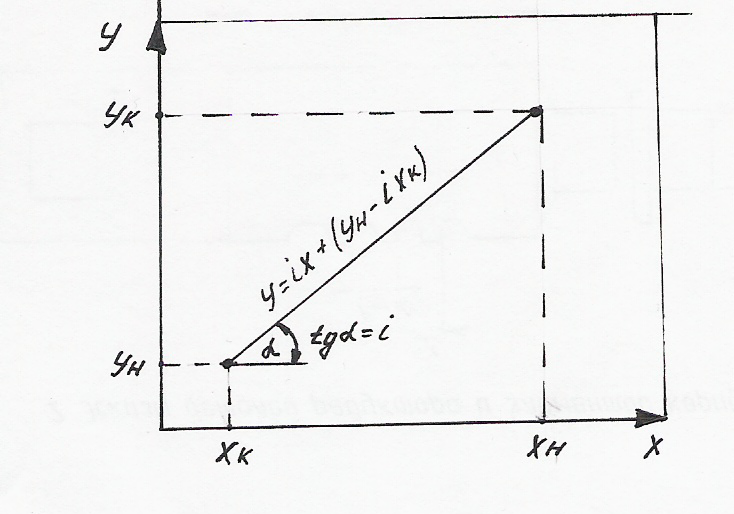
При х=х и у=у уравнение рабочей линии приводится к уравнению (1).

При противотоке может быть обеспечена достаточно большая разность концентраций у и х в потоках покидающих аппарат. В этом состоит одно из преимуществ противоточного контактирования фаз.

В случае прямотока общий материальный баланс для аппарата записывается, как и для противотока, в виде уравнения (1).

схема потоков график изменения концентраций вдоль

поверхности контакта фаз

Уравнение рабочей линии может быть получено при рассмотрении материальных потоков для части аппарата ниже сечения 1-1:

Отсюда получим уравнение рабочей линии для прямотока

(3)

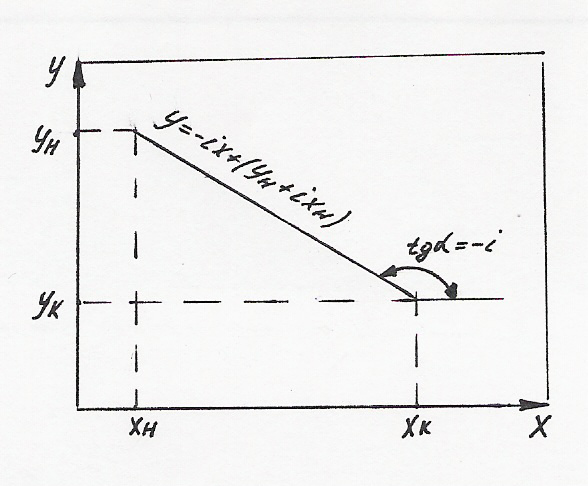
Таким образом, в отличие от противотока, при прямотоке тангенс угла наклона рабочей линии отрицателен.

Отличительной особенностью прямоточного процесса является то обстоятельство, что в пределе выходные концентрации у и х стремятся к равновесию. Поэтому большую разность этих концентраций обеспечить не удается.

В этой связи прямоток обычно создают в пределах отдельного контактного устройства, тогда как в целом в аппарате реализуется противоток.

Общий материальный баланс для случая перекрестного тока, аналогичен противотоку и прямотоку.

Если ввести относительную координату , , где H – общая длина контактной зоны, то для произвольного сечения 1-1 можно составить следующий покомпонентный материальный баланс, подразумевая под среднюю концентрацию на выходе из рассматриваемого участка контактной зоны:

Отсюда получим уравнение рабочей линии для случая перекрестного тока:

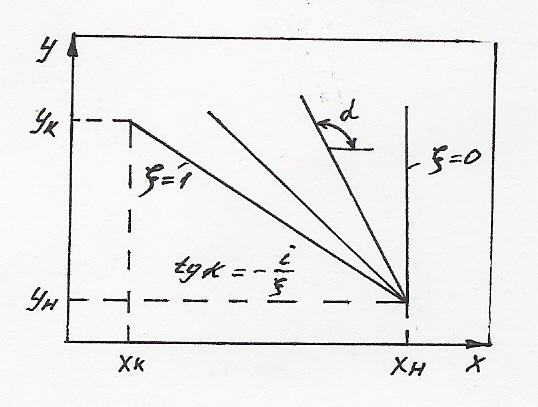
(4)

Как и в случае прямотока, при перекрестном токе рабочая линия имеет отрицательный тангенс угла наклона, величина которого зависит от положения рассматриваемого сечения в контактной зоне. При этом все рабочие линии, соответствующие любому , проходят через точку . Разбив контактную зону на несколько участков, можно получить изменение концентраций вдоль контактной зоны.

Поскольку при перекрестном токе изменение концентраций в пределах контактной зоны определяется совокупностью рабочих линий, условия равновесия на выходе из аппарата уже не оказывают столь сильного влияния на величины концентраций и . Поэтому при перекрестном токе в пределах контактной зоны обеспечивается большее изменение концентраций, чем при прямотоке. В этом отношении перекрестный ток занимает промежуточное положение между прямотоком и противотоком, приближаясь к противотоку.

5.1.7. Средняя движущая сила диффузионного процесса и число единиц

переноса

Как следует из основного уравнения массопередачи, средняя движущая сила процесса определяет количество переданной массы вещества. Поскольку рабочие и равновесные концентрации изменяются вдоль поверхности контакта фаз, необходимо рассчитывать среднюю движущую силу процесса.

Из основного уравнения массопередачи поверхность фазового контакта определяется следующим образом:

или (1)

Для вычисления, например, напишем дифференциальные уравнения материального баланса фазы G и массопередачи:

и

откуда

С другой стороны

т.е.

Интегрируя последнее выражение в пределах изменения концентраций в аппарате, получим:

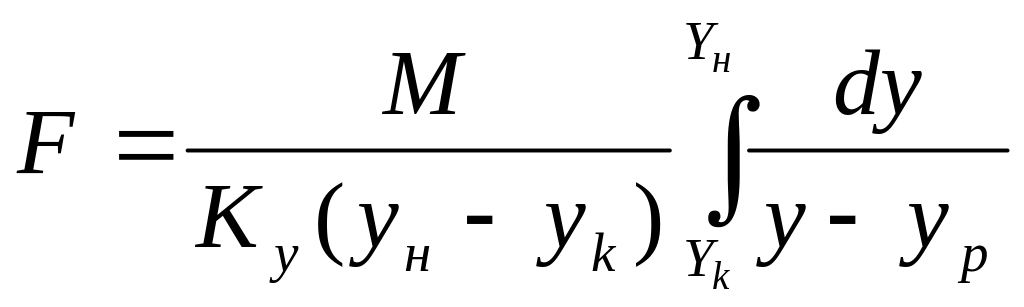(2)

Сравнив это выражение с уравнением (1) получим:

(3)

Написав дифференциальное уравнение материального баланса и уравнение массопередачи для фазы L и проинтегрировав его, получим:

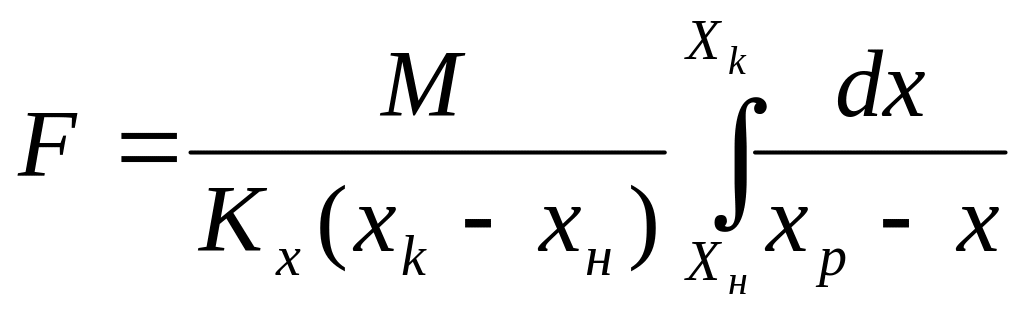(4)

Сопоставляя найденное с уравнением (1) имеем:

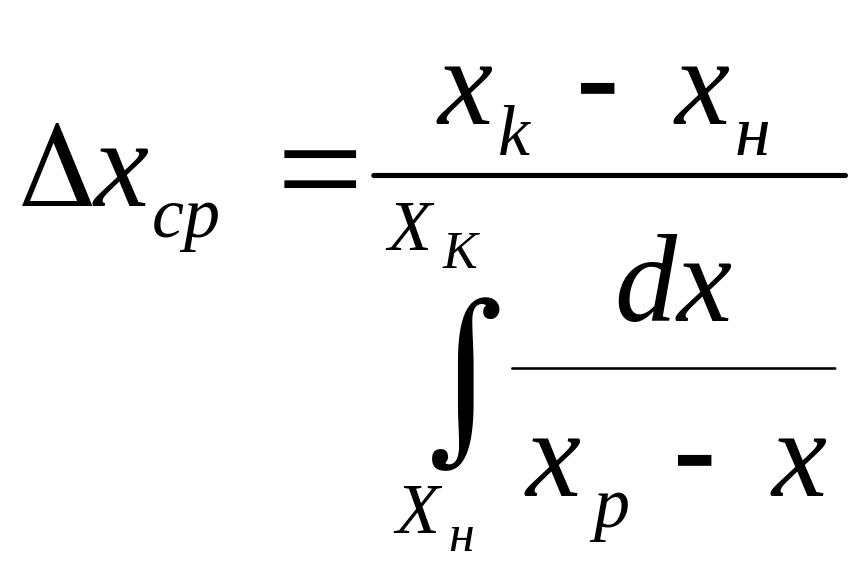(5)

При практическом применении получены равенств интегралы в этих выражениях могут быть найдены численным или графическим интегрированием. С этой целью для ряда значений находят соответствующие им величины и . Затем в координатах , строят кривую площадь Sy под которой между ординатами и в соответствующем масштабе и определяется искомый интеграл.

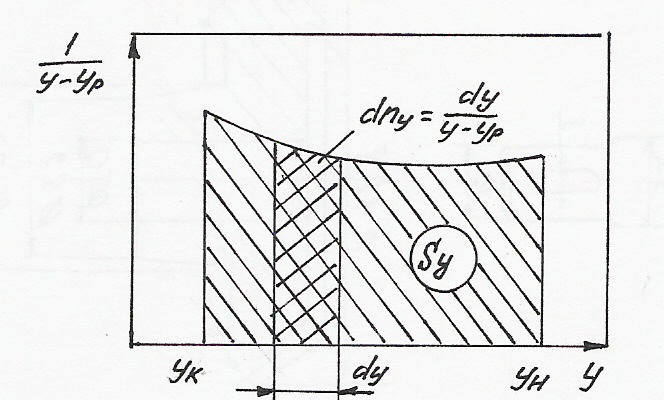
Интегралы

представляют собой изменение концентраций в пределах контактной зоны, приходящейся на единицу движущей силы, и называются числом единиц переноса. Они используются при расчетах различных массообменных процессов.

5.1.8. Массообмен в системах с твердой фазой

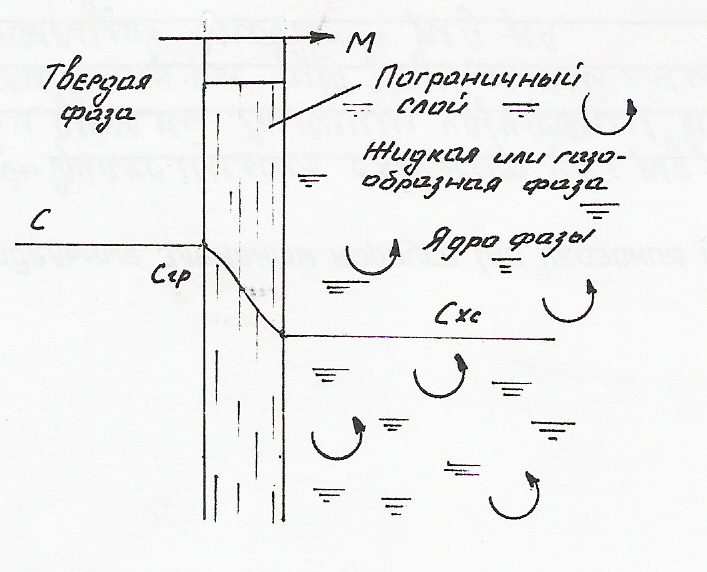
Концентрация компонента внутри твердого вещества уменьшается в направлении к поверхности раздела фаз. Перемещение вещества к границе раздела фаз происходит по законам массопроводности, являющихся аналогом законов молекулярной диффузии для жидкостей и газов. У поверхности твердой фазы возникает пограничная пленка жидкости (газа) толщиной , в пределах которой перенос вещества осуществляется молекулярной диффузией.

На внешней границе пленки, сопрягающейся с ядром потока жидкой фазы, происходит выравнивание концентраций в ядре потока Сж. В ядре потока жидкости концентрации выравниваются за счет конвективной и молекулярной диффузии.

При переходе вещества из твердой фазы его содержание в этой фазе будет непрерывно уменьшаться как во времени, так и по направлений к границе раздела фаз. Поэтому все процессы с участием твердой фазы являются нестационарными.

Диффузия передаваемого компонента в твердой фазе происходит аналогично молекулярной диффузии и уравнение массопроводности записывается аналогично закону Фика:

(1)

где К – коэффициент массопроводности, аналогичный коэффициенту

молекулярной диффузии D.

Количество вещества, перешедшее в ядро потока жидкости, определяется уравнением конвективной диффузии:

(2)

Поскольку на границе раздела фаз вещество не накапливается и не исчерпывается, то из уравнений (1) и (2) получим:

Разделив правую часть этого уравнения на левую, получим диффузионный критерий Б и о для массообменных процессов в присутствии твердой фазы:

(3)

Аналогично уравнению молекулярной диффузии можно получить следующее дифференциальное уравнение массопроводности:

(4)

При делении левой части последнего уравнения на один из членов правой части, получим диффузионный критерий Фурье для процесса массопередачи в твердой фазе:

(5)