1.3 Закон сохранения массы и энергии. Энергетический и материальный балансы

Законы сохранения массы и энергии, открытые Ломоносовым, Лавуазье, Майером и Джоулем, играют в науке о процессах и аппаратах основную роль. Они устанавливают, что в природе и технике имеют место только такие превращения, при которых масса и энергия внутри системы остаются неизменными. В науке о процессах и аппаратах эти законы приобретают форму материальных и энергетических балансов.

Материальный баланс, основанный на законе сохранения массы, составляют для определения расхода исходных веществ или выхода готовых продуктов.

Предположим, что в аппарате, в соответствии с рисунком 1.1, совершается какой-либо процесс. В этот аппарат поступают компоненты А.В.С.

Рис. 1.1 и 1.2.

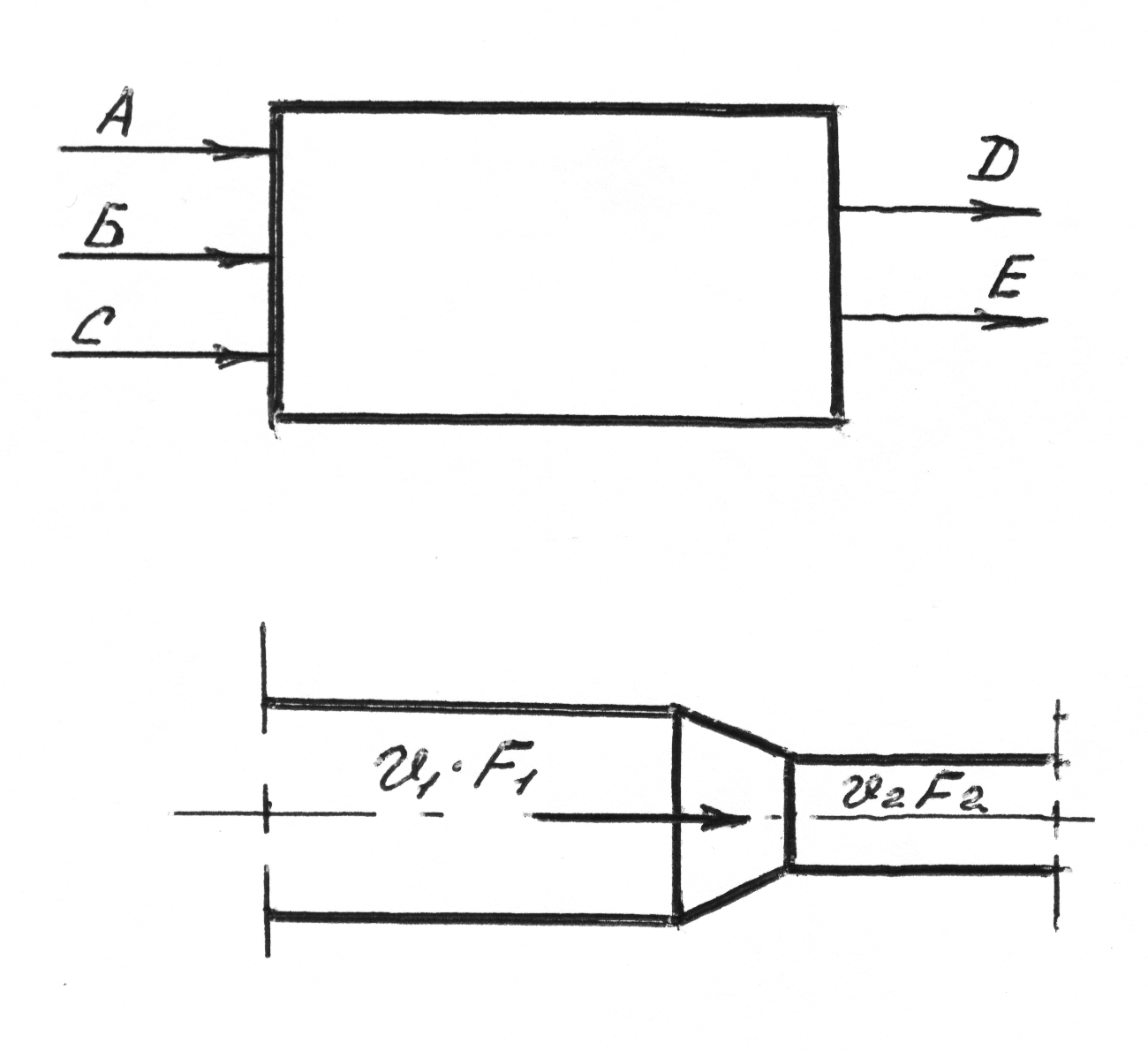
Это могут быть газы, пары, жидкости или твердые тела. В результате процесса, протекающего в аппарате, из него выходят вещества D и Е. Очевидно, что общее массовое количество веществ, входящих в аппарат, не может быть больше или меньше количества веществ выходящих из аппарата. Это вытекает из закона сохранения материи. Из изложенного следует равенство

,

где m – масса компонентов, а уравнение носит название материального баланса.

Для систем, находящихся в движении (поточных систем), закон сохранения массы представляется уравнением неразрывности. Для двух сечений аппарата F₁ и F₂, в соответствии с рисунком 1.2, со скоростями потока V₁ и V₂, имеет силу уравнение неразрывности

Энергетический баланс составляют на основе закона сохранения энергии, согласно которому при любом процессе приход энергии (тепловой, механической или электрической) равен расходу ее.

Рис. 1.3.

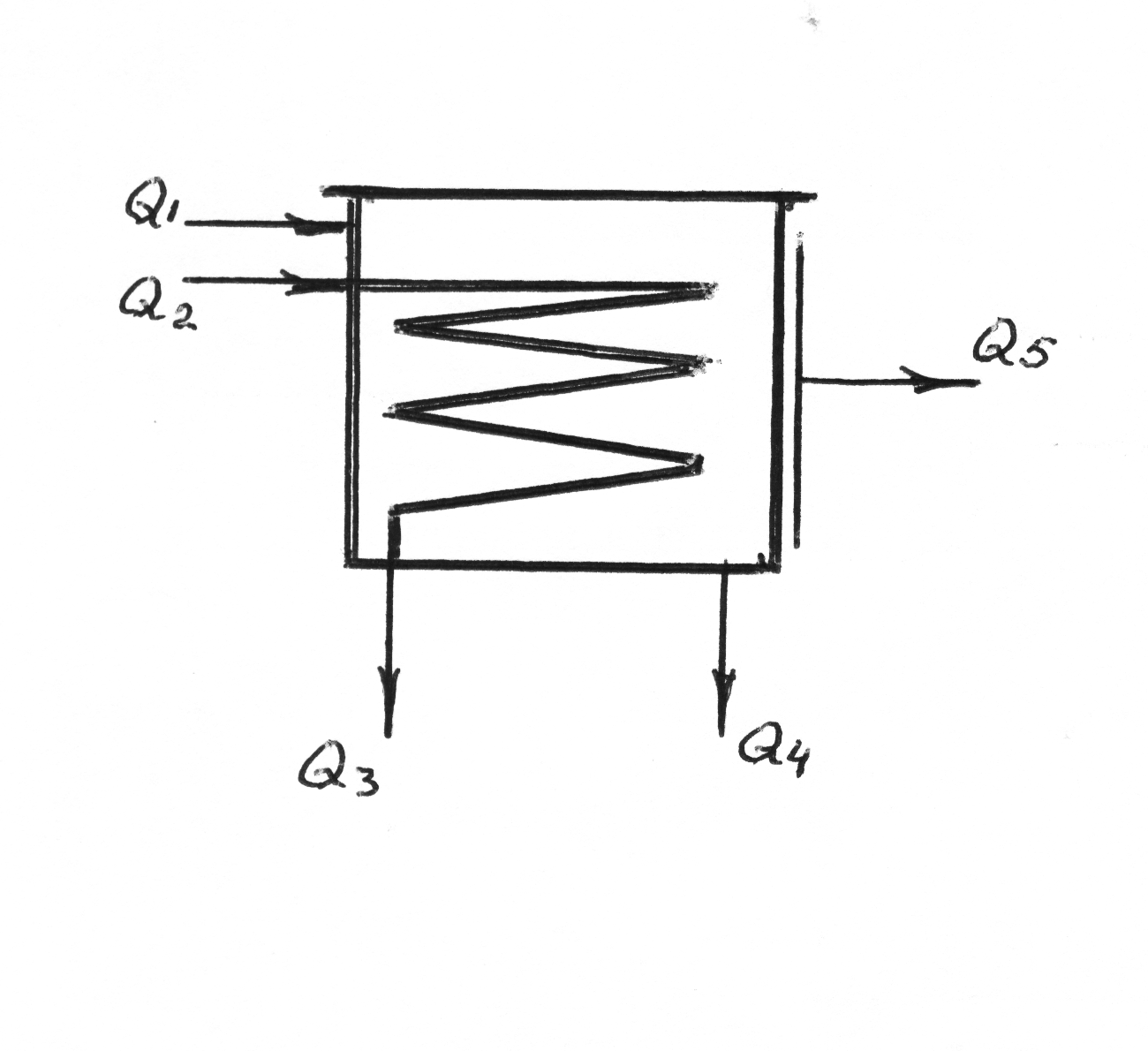
Например, для аппарата, в котором жидкий продукт нагревается паром, уравнение теплового баланса при условии полной конденсации пара запишется в виде

,

где Q₁ и Q₂ – количество тепла введенного в аппарат с продуктом и паром, Дж;

Q₃ и Q₄ – количество тепла выведенного из аппарата с конденсатом и продуктом, Дж;

Q₅ – количество тепла, теряемого стенками аппарата в окружающую среду, Дж.

При проектировании нового аппарата из уравнения обычно определяют количество тепла Q подводимого с паром, а по нему находят расход пара. При исследовании действующих аппаратов находят потери тепла Q₅ в окружающую среду.

1.4 Законы переноса массы и энергии. Принцип движущей силы

Для анализа и расчета процессов необходимо, кроме данных материального и энергетического балансов, знать интенсивность процессов и аппаратов. При рассмотрении процессов различной природы (гидродинамических, тепло- и массообменных) было замечено, что их кинетические уравнения аналогичны.

Для тепловых процессов кинетическое уравнение, известное из курса термодинамики, имеет вид

,

где Q – количества тепла, Дж;

F – поверхность теплообмена, м²;

– время, с;

к – коэффициент теплопередачи (теплопроводимости), Вт/(м² к);

– разность температур (движущая сила процесса);

R = 1/k – термическое сопротивление (сопротивление переносу тепла.

Для массообменных процессов кинетическое уравнение имеет аналогичный вид

,

где dm – масса вещества, переданного за время , кг;

F – площадь поверхности массообмена, м²;

– коэффициент, характеризующий интенсивность передачи массы (коэффициент проводимости), кг/(м² с кг/м³);

– движущая сила процесса массопередачи, выражаемая разностью концентраций, кг/м³;

– сопротивление массопередаче.

Для гидродинамических процессов, например, для фильтрации, кинетическое уравнение может быть записано в виде

,

где V – объем фильтрата, м³;

F – площадь поверхности фильтрата, м²;

R₂ – гидравлическое сопротивление фильтрата;

– коэффициент проводимости фильтрующей среды – величина, аналогичная К и ;

– движущая сила процесса, выражаемая разностью давлений, Па.

Таким образом, все рассмотренные кинетические уравнения могут быть приведены к единообразному виду

,

где J – скорость протекания процесса;

– движущая сила процесса, всегда представляющая разность некоторых величин (давления, температуры, концентрации);

l – коэффициент проводимости – некоторая скалярная величина, характерная для рассматриваемого процесса и обратная величине сопротивления.

Анализ кинетических уравнений позволяет определить общий принцип интенсификации процессов: для увеличения скорости протекания процесса нужно увеличить движущую силу и уменьшить сопротивление или, что тоже, увеличить проводимость.

Понятие «движущая сила» является основным при рассмотрении любого процесса. Она представляет собой некоторую разницу потенциалов характерную для каждого вида процессов.