3.2 Сепарирование

3.2.1 Классификация и краткая характеристика процессов сепарирования.

Сепарирование – это процесс механического разделения сыпучих материалов на фракции, отличающиеся свойствами частиц.

Цели и способы сепарирования сыпучих продуктов весьма разнообразны:

• очистка от примесей, ухудшающих условия хранения, транспортирование и переработки или снижающих качество готовой продукции;

• сортирование на фракции различного качества для переработки в продукты различного или одинаково назначения;

• извлечение готовых продуктов в процессе переработки и сепарирование промежуточных продуктов переработки для их раздельной обработки на последующих операциях.

Основная цель механического разделения смесей заключается в том, чтобы в процессе сепарирования выделить и сформировать фракции по таким признакам частиц, которые обеспечивают требуемое качество промежуточных и конечных продуктов.

Для механических способов сепарирования сыпучих продуктов используют следующие признаки частиц.

1. Геометрические

а) длина – максимальный размер частицы;

б) ширина – максимальный размер наибольшего по площади сечения, перпендикулярного лини длины;

в) толщина – минимальный размер того же сечения.

2. Форма – оценивается коэффициентом формы в виде отношения длины к толщине.

3. Плотность – отношение массы частицы к ее объему.

4. Упругость – оценивается коэффициентом восстановление нормальной скорости, т.е. отношение проекции скорости частицы после удара о неподвижную поверхность к такой же проекции скорости до удара.

5. Трение о поверхность, оцениваемое коэффициентом сухого трения, т.е. отношением тангенциальной реакции связи к нормальной реакции при относительном движении.

6. Магнитная восприимчивость – оценивается силой, с которой на массу в 1 г. действует магнитное поле с единичной магнитной индукцией и напряженностью.

Для использования различия по этим признакам частиц смеси при ее сепарирование на две и более фракцию применяют различные способы механического воздействия, которые выполняют три основные функции:

1. Обеспечивают непрерывное поступление смеси в рабочее пространство;

2. Заставляют частицы с различными свойствами перемещаться в разные места рабочего пространства;

3. Раздельно удаляют из рабочего пространства полученные фракции.

Для разделения сыпучих продуктов по выше перечисленным признакам применяют сепараторы со следующими рабочими органами: ситами (решетами), ячеистой поверхностью, пневмосепарирующими каналами, магнитами, электростатическими элементами и т.д.

Существующие сепараторы условно подразделяют на простые и сложные. В простых сепараторах смесь разделяют по одному признаку на две фракции, на каком либо одном рабочем органе. Сложные представляют собой соединения нескольких простых сепараторов. В них сепарируют смеси на три и более фракцию по нескольким признакам, при этом разделение может выполняться последовательно, параллельно или комбинировано.

Наибольшее распространение получили сепараторы с плоскими рабочими органами, совершающими различного рода колебания, обеспечивающие относительное движение частиц.

2. Теоретические основы вибрационного перемещения.

Вибрация – это наиболее распространенный вид механического воздействия на сыпучий материал при его сепарировании.

При вибрационном сепарирование сыпучего материала, скорость подачи – это основной параметр от которого зависят производительность и эффективность процесса сепарирования. Поэтому расчетное определение средней скорости частиц сыпучего тела в потоке составляет первоочередную задачу теории вибрационного перемещения.

Описать движение сыпучего материала практически невозможно, поэтому, как правило, дифференциальные уравнения относительного движения составляют для отдельных частиц простейшей формы, и, как показывает многочисленная практика, применение этих формул к расчету вибрационного перемещения сыпучих тел дает вполне удовлетворительную точность в достаточно больших пределах параметров процесса.

Для сближения результатов применения теории вибрационного перемещения отдельной материальной частицы с действительной картиной движения сыпучих тел много значат методы экспериментального определения коэффициентов отражающих в расчетных формулах свойства частицы опорной вибрирующей поверхности. При движении без подбрасывания такими коэффициентами служат коэффициенты трения скольжения и покоя, а при движении с подбрасыванием – также коэффициенты мгновенного ударного трения и восстановления нормальной скорости.

3.2.3 Перемещение частицы по опорной наклонной плоскости.

Согласно закону сухого трения при относительном движении двух соприкасающихся тел, сила трения приложенная к каждому из них, противоположна его относительной скорости и пропорциональна нормальной реакции.

Рис. 3.8.

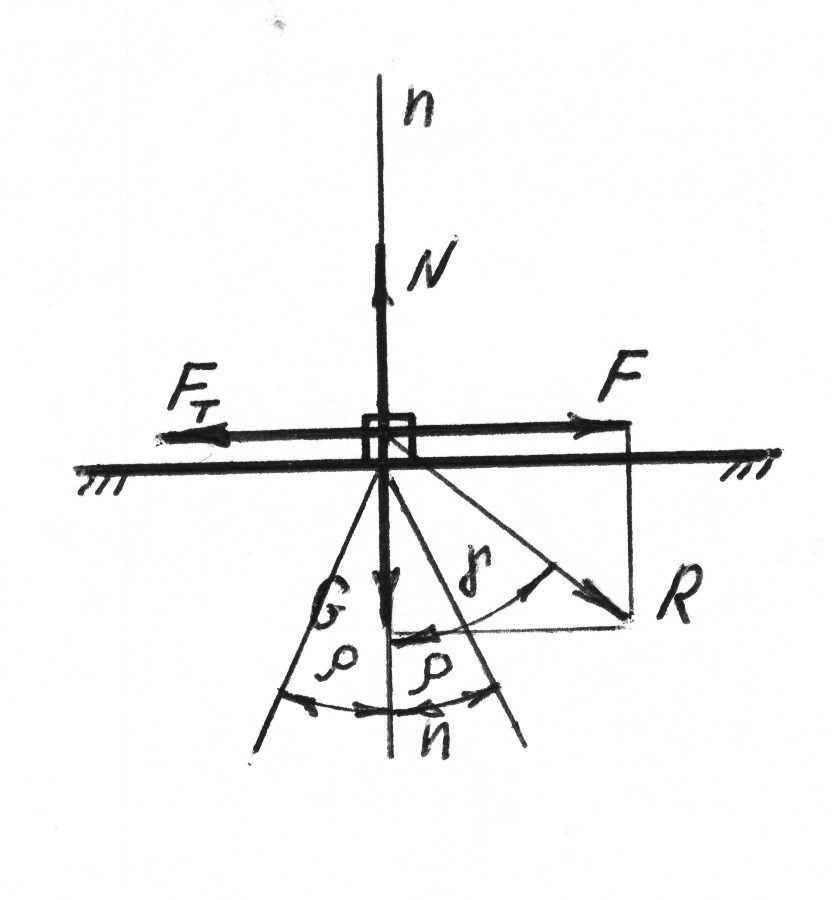
Частица материала, находящаяся на шероховатой поверхности может выйти из состояния покоя только в том случае, если тангенциальная проекция F равнодействующей R внешних сил больше предельного значения силы трения . Иначе говоря, движение частицы начинается, когда равнодействующая R внешних сил образует с нормалью п - п угол , больший угла трения . Если , то равновесие частицы не нарушается. Случай соответствует предельному равновесию, а при наличии начальной скорости – равномерному движению.

Рассмотрим материальную частицу на неподвижной наклонной плоскости, образующей с горизонталью угол .

Пока на частицу, находящуюся в покое действует внешняя сила G = mg, уравновешивающая ее полная реакция связи образует с нормалью угол меньше угла трения. Из этого состояния частицу можно вывести, приложив добавочную силу F, линия действия которой h – h образует с наклонной плоскостью угол . При этом необходимо, чтобы линия равнодействующей сил G и F выходили за пределы угла трения .

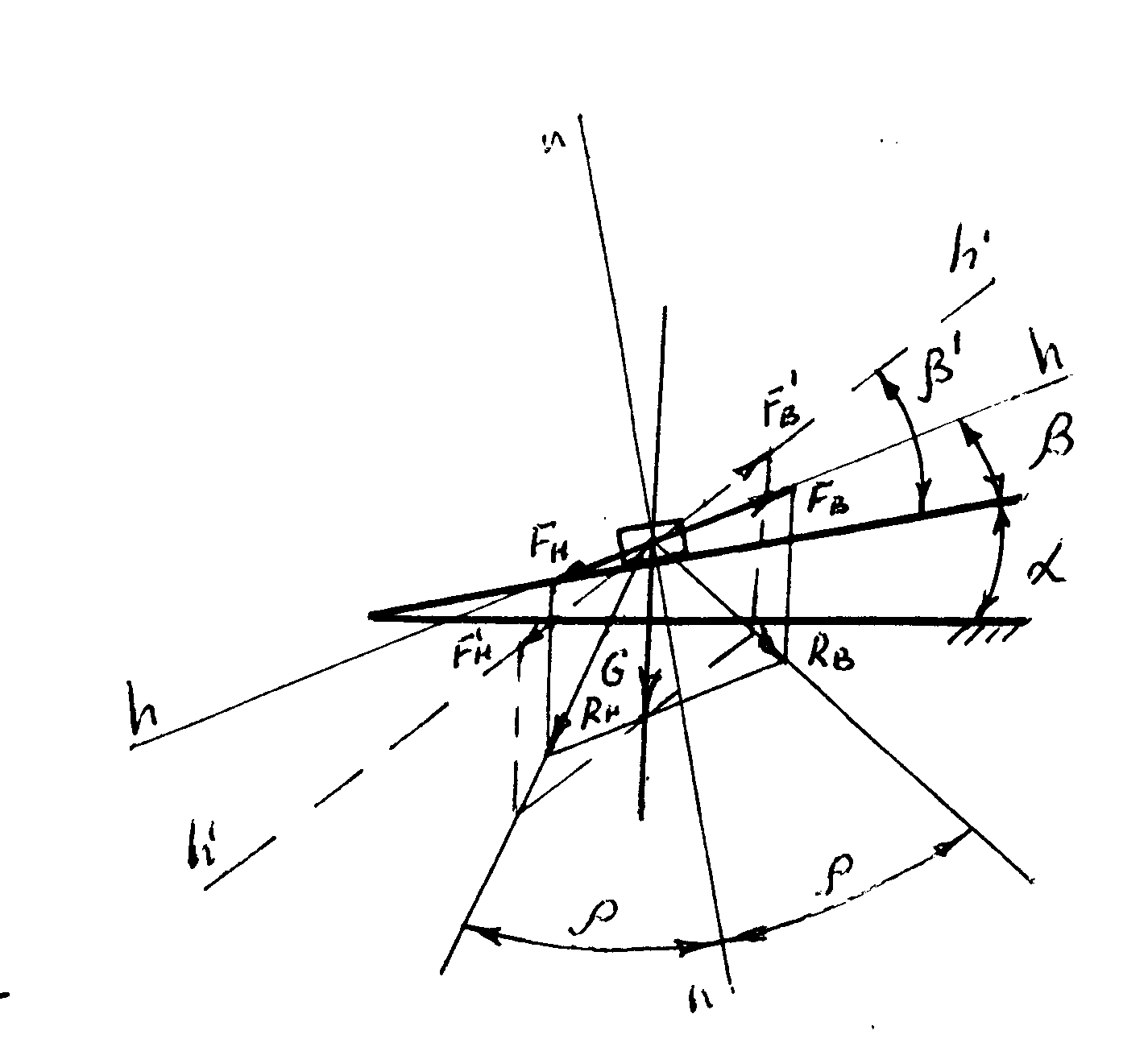
Рис. 3.9.

Определим предельные добавочные силы F_в и F_н…. Если добавочная внешняя сила F направлена вверх по прямой h - h и больше силы F_в, то частица начинает ускорено двигаться вверх, если же сила F направлена вниз и больше силы F_н, то частица начинает ускоренно двигаться вниз.

В рассматриваемом случае /F_в/ > /F_н/, то есть для перемещения частицы вверх необходимо приложить большую силу F, чем для движения вниз.

Если сила F – непрерывная периодическая знакопеременная функция времени, подчиняющаяся гармоническому закону, то можно выбрать ее амплитудное значение /F_m/, удовлетворяющее условию /F_н/ < /F_m/ < /F_в/. В этом случае движение частицы вверх начаться не может, и за каждый период изменения силы F она получит перемещение вниз, чередующееся с состоянием покоя.

Если удовлетворяется условие /F_m/ > /F_в/ > /F_н/, то за один период изменения силы F частица переместится один раз вниз и один раз вверх. При этом перемещение вниз будет больше, так как /F_в/ > /F_н/ и условия начала движения частицы вниз (/F/ > /F_н/) выполняются в течение большего времени, чем условия начала движения вверх (/F/ > /F_в/). В зависимости от соотношения сил F_m, F_н и F_в интервалы движения частицы вниз и вверх могут быть разделены одним или двумя интервалами покоя. Интервал покоя (пауза) после одного из перемещений наступает тогда, когда частица остановилась раньше, чем возникли условия для ее движения в противоположном направлении. По мере увеличения амплитудного значения F_m добавочной силы F интервалы покоя уменьшаются, и наступает периодический режим без пауз, при котором перемещения в противоположных направлениях разделены мгновенными остановками.

Рассмотренные режимы движения частицы при условии /F_в/ > /F_н/ характерны преобладанием перемещений вниз, следствием чего будет направленное в среднем движение вниз, с непрерывной скоростью V_n, рассчитываемой по уравнению

,

где – перемещения частицы соответственно вниз и вверх за один период изменения силы F_y м;

Т_о – период изменения силы F, с;

п – число периодов изменения силы F за 1 мин.

Одним из важнейших параметров, влияющих на режим перемещения частицы, служит угол , характеризующий ориентацию линии действия добавочной силы.

С увеличением угла до изменяется соотношение между предельными значениями добавочных сил: теперь возникает неравенство и преобладающим будет перемещение частицы вверх при возможности воспроизведения периодических режимов, аналогичных рассмотренным ранее.

Приведенные рассуждения относились к режимам движений частицы без подбрасывания, когда контакт ее с плоскостью обеспечивается все время. Это условие выполняется, если равнодействующая R сил G и F не поднимается выше наклонной плоскости, постоянно прижимая к ней частицу.

3.2.4 Перемещение частицы без подбрасывания, при прямолинейных гармонических колебаниях опорной плоскости.

Рассмотрим относительное движение частицы массой m в переносной системе координат х, у, жестко связанной с колеблющейся плоскостью.

Рис. 3.10.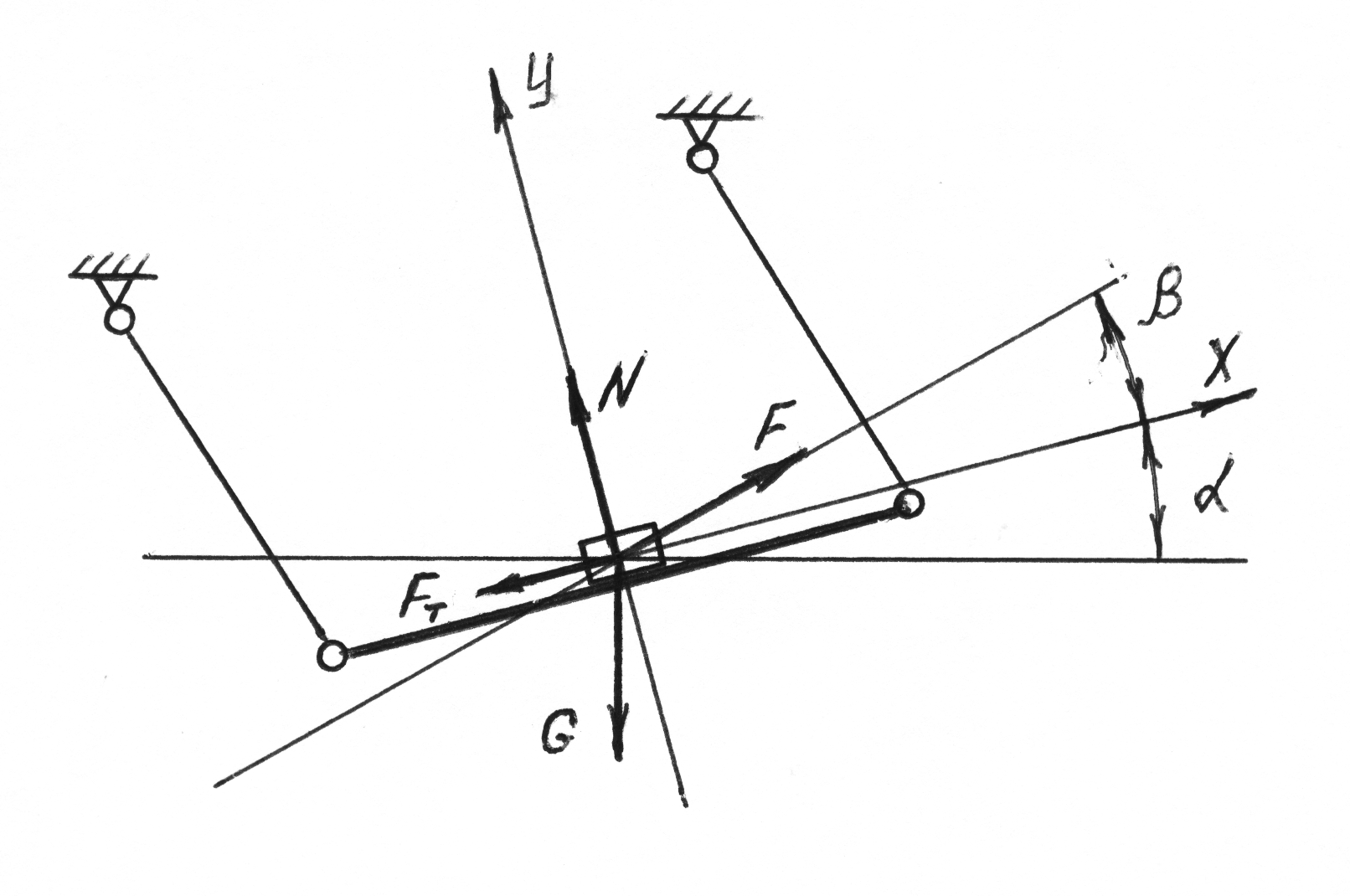

Для этого, к действующим на частицу силам и реакциям связи присоединим переносную силу инерции , выполняющую роль добавочной силы.

Составим уравнения относительного движения частицы для случая, соответствующего движению в положительном направлении оси Х.

(1)

(2)

При гармонических колебаниях наклонной плоскости переносное ускорение

,

поэтому .

(3)

(4)

Для относительного движения без подбрасывания y = const и ; что позволяет из формулы (4) определить нормальную реакцию N.

(5)

Если нет подбрасывания, реакция N должна сохранить положительное направление за весь период колебания, даже когда второй член правой части равенства (5) принимает максимальное значение . Поэтому условие безотрывного движения частицы имеет вид N > 0 или

(6)

Подставляя значение N из формулы (5) в (3), после сокращения на m и элементарных преобразований получим

Заменяя , приведем это уравнение к следующему виду

(7)

Если направление относительной скорости частицы противоположно рассмотренному, то в уравнении (1) знак (–) перед силой F_тр нужно заменить на знак (+).

В этом случае после преобразований, аналогичных выполненным придем к уравнению

(8)

Обобщая уравнения (7) и (8), представим их в следующем виде

, (9)

где ,

, (10)

(11)

В равенствах (9), (10) и (11) верхние знаки у а, Z и верхние знаки перед относятся к случаю положительного направления относительной скорости частицы (х > 0), а нижние – к случаю отрицательного направления (х < 0).

Положительные значения углов и соответствуют показанным на рисунке. Изменение направления этих углов должно сопровождаться изменением знака перед ними в формулах (10) и (11).

Предельно возможные условия начала скольжения частицы в обоих направлениях и характер установившегося периодического относительного движения по вибрирующей плоскости определяется значениями безразмерных параметров Z₊ и Z_-. Области существования возможных режимов, совпадающие с областями устойчивости относительного движения без подбрасывания, определяются по диаграмме И.И. Блехмана.

Режим 1 – соответствует двустороннему скольжению частицы с двумя паузами;

Режим 2 – двустороннему скольжению частицы без пауз (с двумя мгновенными остановками);

Режим 3 – двустороннему скольжению частицы с одной паузой и одной мгновенной остановкой;

Режим 4 – скольжение частицы только в одном из направлений с одной паузой.

Наиболее благоприятным для процесса сепарирования, является режим 2, обеспечивающий непрерывное движение сыпучего продукта по рабочему органу и наиболее эффективное его разделение на фракции.

3.2.5 Перемещение частицы при круговых колебаниях горизонтальной опорной плоскости.

Рассмотрим плоскую материальную частицу массой m на шероховатой горизонтальной поверхности, совершающей круговые колебания с частотой и амплитудой – радиусом R в горизонтальной плоскости.

Относительному движению частицы по поверхности препятствует сила трения, предельное значение которой F_mp = mqf. Частица движется вместе с поверхностью (без относительного движения), пока сила инерции не превосходит предельной силы трения F_mp. Поэтому условие относительного покоя будет

(1)

Рис. 3.11.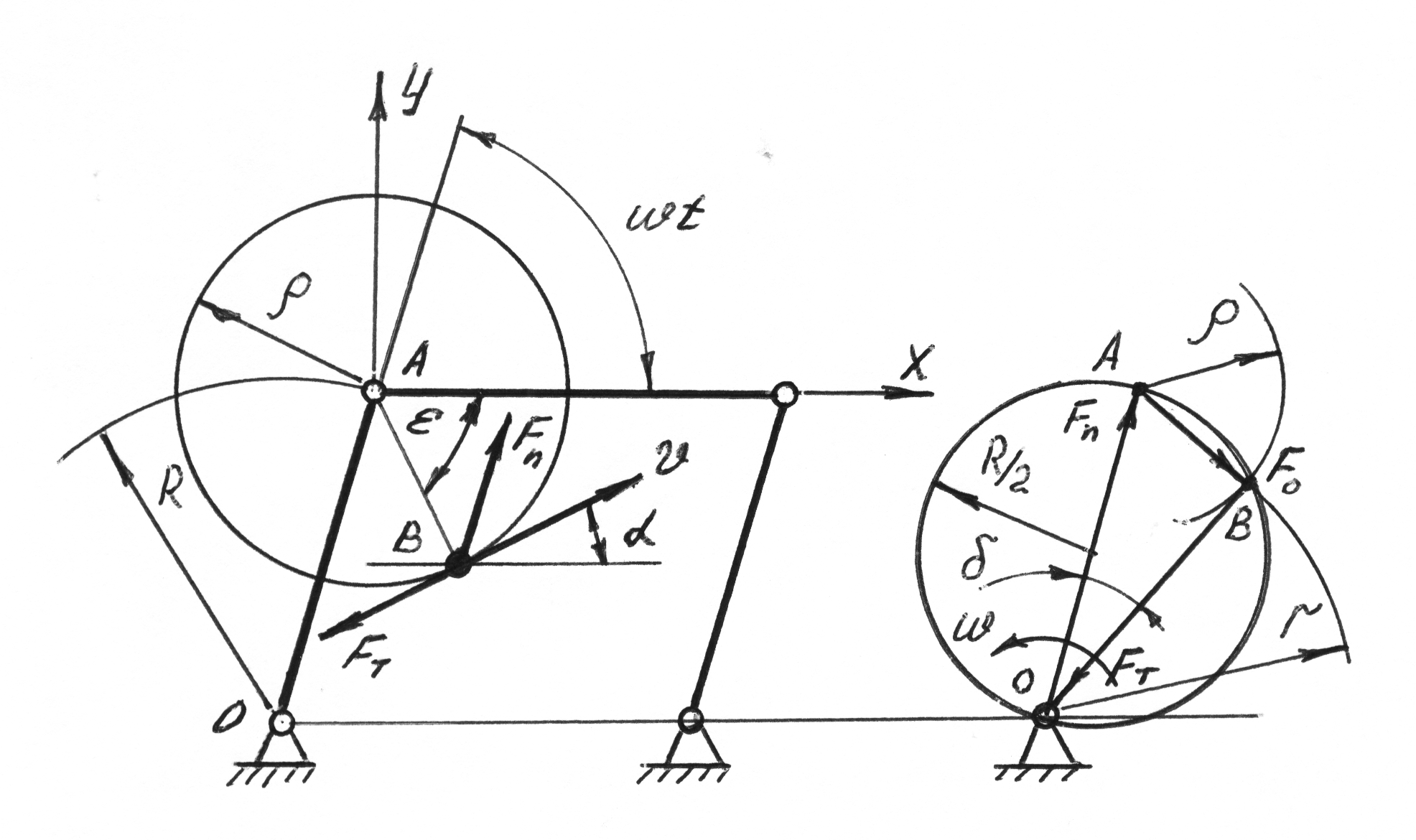

Максимальное значение центростремительного ускорения, сообщаемого частице силой трения, составляет

(2)

Рассмотрим относительное движение частицы в координатной системе х, у, принадлежащей опорной поверхности. Учтем действие на частицу переносной силы инерции и силы трения , направленной противоположно вектору скорости в относительном движении и поэтому образующей с осью х угол , причем

;

Дифференциальные уравнения относительного движения частицы:

или

, (3) (4)

Частные решения уравнений (3) и (4), соответствующие предельному движению частицы, к которому она стремится с течением времени, следующие:

(5)

(6)

Дифференцируем формулы (5) и (6) по времени

(7)

(8)

(9)

(10)

После подстановки и в уравнение (3) получим

(11)

Положим , (12)

тогда

или (13)

Уравнение (13) образуется в тождество, если

(14)

(15)

Определим из уравнения (12)

и учитывая уравнение (14) получим

(16)

Таким образом, при постоянных относительное движение частицы проходит по окружности радиусом с отставанием по фазе от переносного движения на угол .

Абсолютное движение также происходит по окружности, причем единственной силой, действующей на частицу в горизонтальной плоскости, будет сила трения , создающая постоянное центростремительное ускорение , где r – радиус траектории частицы в абсолютном движении.

Имеем , откуда

(17)

Представляет интерес простая геометрическая интерпретация полученного результата. Векторное уравнение динамического равновесия частицы по принципу Даламбера запишем в следующем виде

(18)

где - сила инерции частицы в абсолютном движении, которую можно разложить

(19)

и переписать уравнение (18):

(20)

где - сила инерции в переносном движении;

- сила инерции в относительном движении.

В векторном треугольнике сил (рис. б), вектор силы трения направлен против относительной скорости v, по касательной к окружности радиусом и поэтому перпендикулярной ему, а, следовательно, и центробежной силе F_о в относительном движении. Вершина В прямого угла между векторами и лежит на окружности, построенной на векторе , как на диаметре. Согласно уравнению (18), = - , поэтому уравнение (20) можно представить так:

, или

(21)

Умножая все слагаемые уравнения (21) на или , можно получить соотношения соответственно между векторами скоростей и ускорений частицы в переносном, относительном и абсолютном движениях.

Таким образом, векторный треугольник можно рассматривать как план скоростей и ускорений в соответствующих масштабах.

При постепенном увеличении ускорения (например, вследствие увеличения при ) от 0 до , относительного движения нет, и точка В совпадает с точкой А. При дальнейшем увеличении точка В перемещается по дуге окружности радиусом R/2 от точки А к точке О, с которой совпадает при ; при этом радиус относительной траектории увеличивается, стремясь к R, а радиус абсолютной траектории r увеличивается, стремясь к нулю.

Заметим, что при согласно уравнению (17), радиус абсолютной траектории не зависит от амплитуды R круговых колебаний опорной поверхности, а угол между векторами R и r определяется из условия

,

что совпадает с формулой (14).

3.2.6 Повышение эффективности работы решетных сепараторов

Наряду с плоско-решетными сепараторами применяют сепараторы с цилиндрическими рабочими органами, в которых, выделение частиц проходит под действием центробежных сил, намного превосходящих силу тяжести. Наиболее перспективными, считаются сепараторы с вертикальной осью вращения цилиндра.

Интенсивность процесса сепарирования находится в прямой зависимости от величины скорости движения частицы в пределах отверстия решета.

Введем коэффициент интенсификации

, (1)

где V_ц – скорость движения частицы на выходе из отверстия цилиндрического решета;

V_п – скорость движения частицы на выходе из отверстия плоского решета.

, (2)

где q – ускорение свободного падения;

t_п – время, в течение которого частица проходит путь, равный толщине решета.

, (3)

где - толщина решета, тогда

(4)

Рис. 3.12.

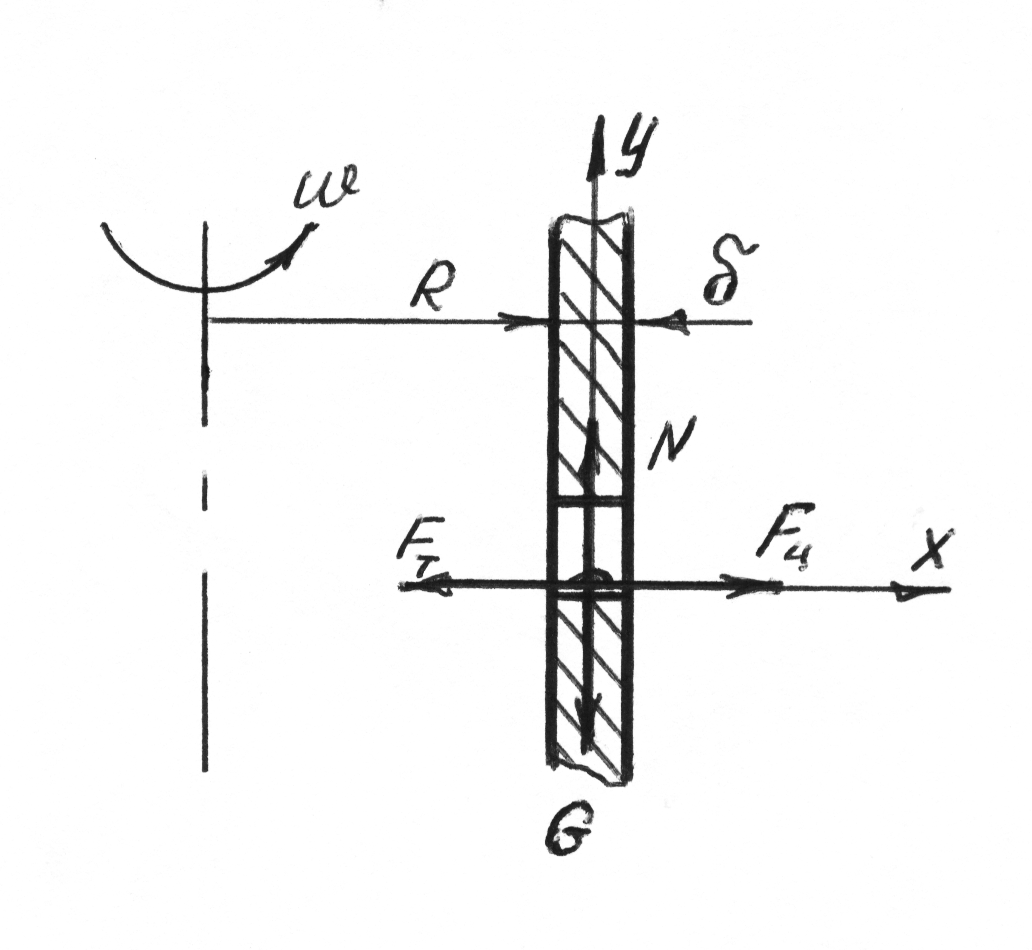
На частицу, находящуюся в отверстии цилиндрического решета действуют:

G – сила тяжести;

F_ц – центробежная сила инерции;

F_тр – сила трения;

N – нормальная реакция.

Сопротивлением воздушной среды и силой инерции в тангенциальном направлении условно пренебрегаем.

Дифференциальное уравнение относительного движения частицы вдоль оси х, имеет следующий вид:

(5)

или

В связи с небольшой толщиной решета считаем, что .

Скорость частицы изменяется от 0 на входе до V_ц на выходе из отверстия за отрезок времени от 0 до t_ц. Сократив на m и интегрируя в указанных пределах, имеем:

(6)

Из выражения (6) видно, что с учетом принятых допущений, движение частицы в пределах отверстия равноускоренное с ускорением . Поэтому по аналогии с (3) можно записать:

(7)

После подстановки (7) в (6) получим:

(8)

Подставляя (8) и (4) в (1), находим

,

или

(9)

Отсюда видно, что степень интенсификации процесса зависит от коэффициента разделения – К.

3.2.7 Перемещение частицы по внутренней поверхности цилиндра вращающегося вокруг вертикальной оси.

Рассмотрим плоскую материальную частицу массой м, находящуюся на внутренней поверхности цилиндра, вращающегося вокруг вертикальной

оси. Рис.3.13.

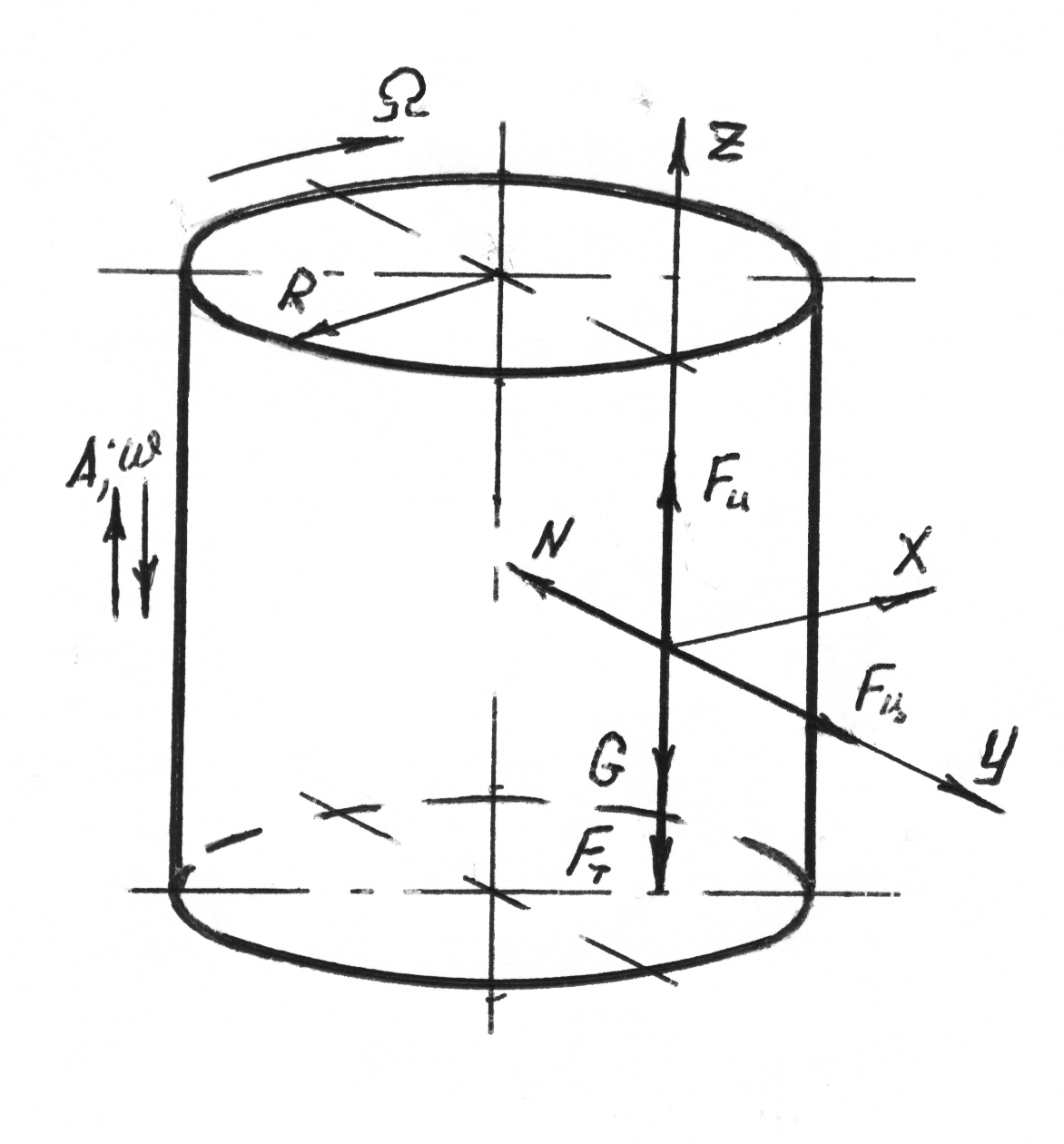
На частицу действуют:

-сила натяжения ;

-центробежная сила инерции ;

-нормальная реакция опоры N;

-сила трения

При относительном движении частицы необходимо, чтобы сила тяжести была больше, чем сила трения т.е.

(1)

В данном случае, нормальная реакция опоры зависит от величины центробежной силы и равна

(2)

Подставляя (2) в (1) получим

или

Откуда, предельное значение угловой скорости вращения цилиндра, при которой возможно относительное движение частицы

(3)

Если (4),

То относительное движение частицы прекращается, и она будет вращаться вмести с поверхностью цилиндра, т.е. совершать переносное движение. В этом случае для того, чтобы частица начала совершать относительное движение, необходимо приложить добавочные силы, т.е. силы инерции.

Для этого цилиндру сообщают различного рода колебания, или сообщают планетарное движение.

Допустим, что цилиндр, совершает гармоническое, возвратно поступательное колебания вдоль оси вращения.

В результате колебаний, возникает сила инерции, величина которой определяется как

(5)

Переносную систему координат XYZ жестко свяжем с поверхностью цилиндра.

Рассмотрим случай относительного движения частицы в положительном направлении оси Z.

Составим дифференциальные уравнения относительного движения частицы в проекциях на оси координат.

(6)

(7)

В ведем условия однозначности и определим нормальную реакцию опоры

у=0; =0; =0.

Из уравнения (7) находим

(8)

Подставляя (8) в (6) и сокращая на массу получим

Или

(9)

При относительном движении частицы в отрицательном направлении оси Z, знаки перед силами и получается на противоположные.

3.2.8 Цилиндрические рабочие органы с дополнительными устройствами

На различных предприятиях пищевых производств встречается большое количество машин с цилиндрическими рабочими органами, внутри которых имеются дополнительные устройства в виде различного рода направляющих, полок, ячеек и т.д.

Рис.3.14.

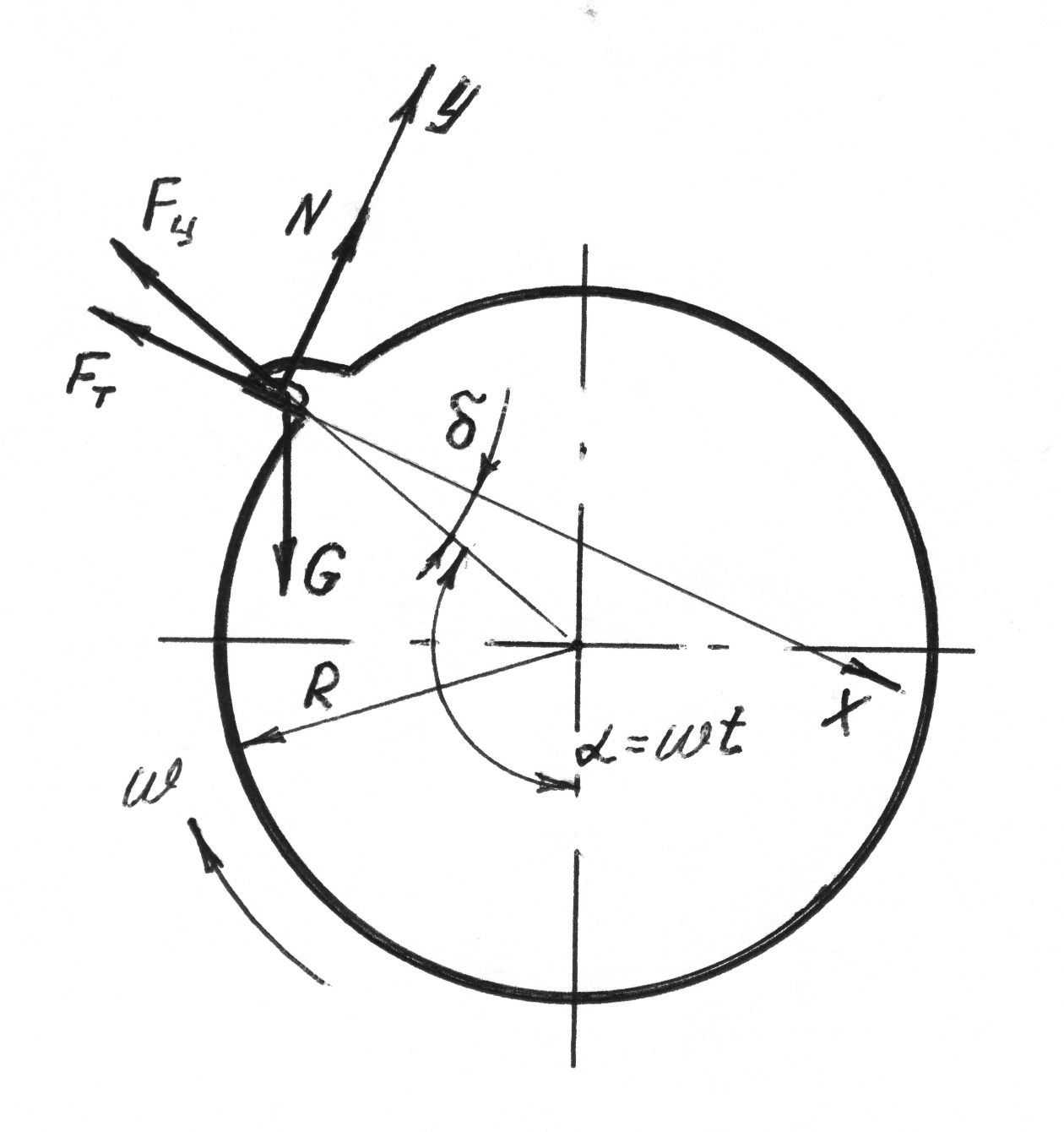
Рассмотрим движение частицы попавшей в ячейку цилиндрической ячеистой поверхности, которая применяется для разделения сыпучего продукта по длине частиц.

Определим положение несущей стенки ячейки углом между несущей стенкой и радиусом цилиндра.

Этот угол по абсолютной величине не изменяется во времени, а зависит от формы и ориентации штампованных ячеек на цилиндрической (триерной) поверхности.

Рассмотрим условие равновесия частицы в ячейке. За подвижную систему координат примем X O Y и запишем уравнение суммы сил в проекциях на оси координат, приравняв их к нулю.

(1)

(2)

Определим нормальную реакцию N из уравнения (2) и подставим в (1)

(3)

(4)

После несложных преобразований и подстановки , получим

или

(5)

и окончательно

(6)

В современных цилиндрических триерах со штампованными ячейками угол близок к нулю, в связи с чем, выражение (6) принимает более простой вид

(7)

Этими выражениями можно воспользоваться для определения угла выпадения частицы из ячейки и рассчитать положение желоба для вывода отсепарированных мелких частиц.

3.2.9 Дисковые ячеистые поверхности. (Дисковые триеры).

Помимо цилиндрических ячеистых поверхностей, для разделения сыпучего продукта по длине частиц, используют дисковые ячеистые поверхности. Ячейки, расположенные с обеих сторон диска по концентрическим окружностям, захватывают короткие частицы и выносят их из общей массы продукта.

Рассмотрим некоторые теоретические предпосылки к определению углов выпадения коротких частиц из ячеек.

Рис.3.15.

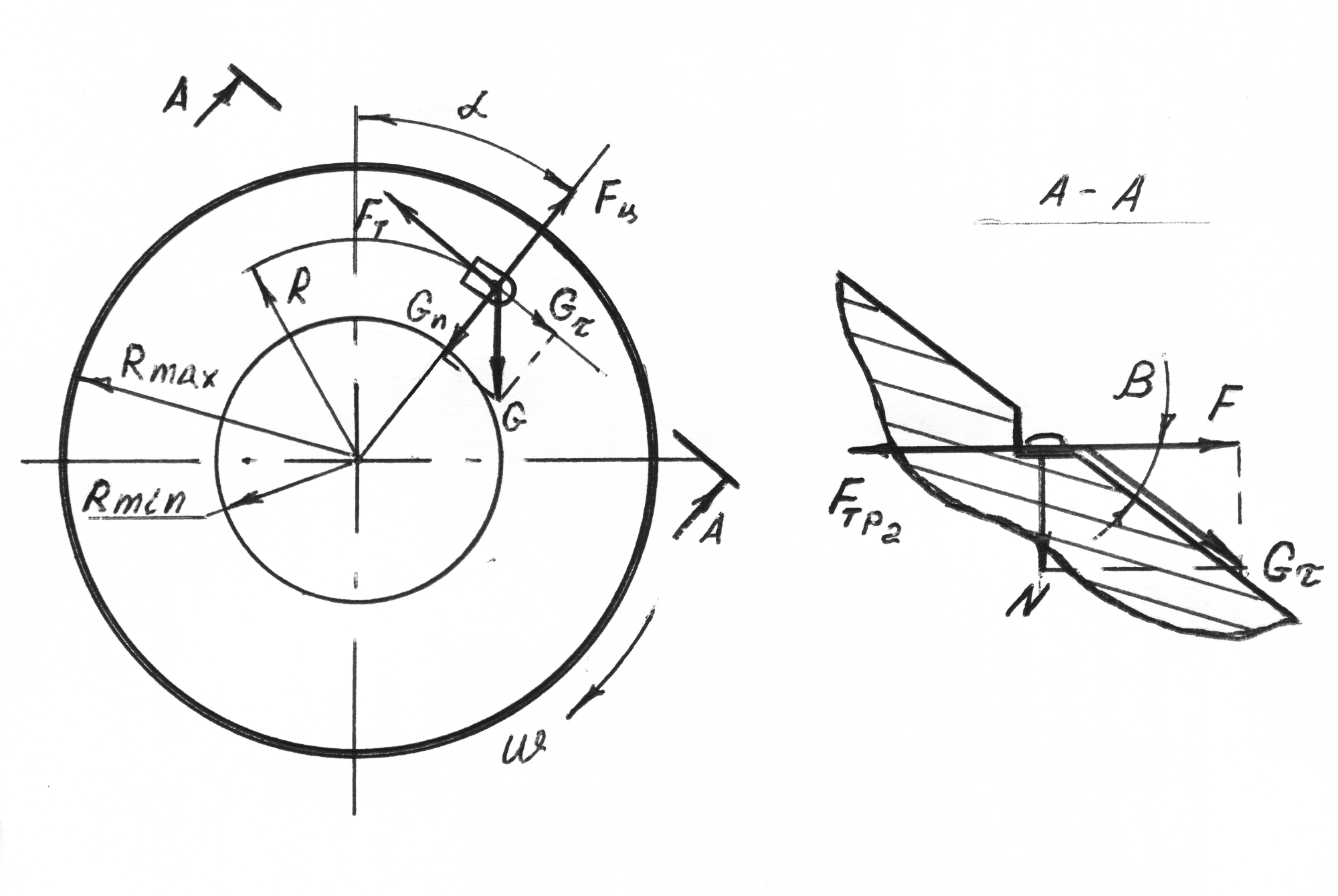
На частицу, находящуюся в ячейке, положение которой определяется радиусом-вектором R, действуют: центробежная сила инерции F_ц в переносном движении, сила тяжести G и сила трения F_тр1 и F_тр2. Силу тяжести в плоскости диска разложим на нормальную и касательную составляющие – G_n и G_r. В зависимости от соотношения сил F_ц и G_n частица будет прижиматься к внутренней или наружной боковой грани ячейки. Выпадение частицы происходит в плоскости А-А, перпендикулярной к плоскости диска. Здесь на частицу действуют такие силы:

- составляющая силы тяжести, выталкивающая частицу из ячейки;

- сила трения о направляющую поверхность ячейки;

- сила трения о наружную боковую поверхность ячейки, когда ;

- сила трения о внутреннюю боковую поверхность ячейки, когда ;

Равновесие частицы в ячейке сохраняется до тех пор, когда и зависит от расположения ячеек, определяемого радиусом R, и кинематического режима работы триера . Ряды ячеек, расположенных ближе к оси вращения, подчиняются условию K < cos , а ячейки, удаленные к периферии – условию K > cos .

Запишем условие равновесия частицы в общем случае

(1)

После подстановки , и преобразований, получим

(2)

Из этого выражения можно определить как углы выпадения частиц так и угловую скорость триерного диска с учетом заданных или выбранных из конструктивных соображений углов выпадения.

Для определения углов преобразуем выражение (2), введя обозначения

или

, и окончательно

(3)

При K > cos в формуле следует брать знак «плюс» и соответственно при K < cos - «минус».

Предельную частоту вращения диска определяют из выражения (1)

(4)

Частота вращения дисков в серийно выпускаемых триерах составляет 50-55 об/мин.

С увеличением угловой скорости дисков возрастает производительность, однако, как было отмечено ранее, ухудшаются условия выпадения коротких частиц.

Обстоятельства, улучшающие условия выпадения частиц при более высоких скоростях вращения, - это уменьшение коэффициента трения зерновки в ячейке, достигаемое высоким качеством обработки ее внутренней поверхности.