3 Механические процессы

3.1 Измельчение твердых материалов

3.1.1 Сущность и назначение процесса измельчения.

Дробление и размол представляют собой процессы механического измельчения твердых веществ. В результате измельчения значительно увеличивается суммарная площадь поверхности обрабатываемого материала.

Эти процессы широко применяются в различных отраслях пищевых производств для интенсификации протекания различных технологических процессов, сокращение потерь веществ и расхода энергии, а также получение готовой продукции.

В зависимости от вида применяемых усилий, измельчение может производиться раскалыванием, ударом, раздавливанием, истиранием и срезом. Выбор вида механического воздействия зависит от крупности и прочности измельчаемого материала. Часто в измельчающих машинах это достигается сочетанием нескольких усилий, например раздавливания и разрыва, удара и истирания и т.д.

Эффективность измельчения оценивается степенью измельчения, удельным расходом энергии на проведение процесса и удельной нагрузкой на рабочий орган измельчающей машины. Степень измельчения выражают отношением суммарной площади поверхности частиц продукта к суммарной площади поверхности частиц исходного материала.

В зависимости от степени измельчения условно различают:

- измельчение крупное

- измельчение среднее

- измельчение мелкое

- измельчение тонкое

- измельчение коллоидное

Измельчение производится по двум основным схемам – в открытом или замкнутом цикле. При работе по первой схеме весь материал проходит через дробилку только один раз, при работе по замкнутому циклу, большая часть материала проходит через дробилку многократно, т.к. материал с размерами кусков больше допустимого предела возвращается на повторное дробление. Это достигается при соединении дробилки или мельницы с устройствами для разделения измельченного материала по крупности частиц.

Измельчение по замкнутому циклу позволяет значительно увеличить производительность установки и получить более равномерный по крупности продукт.

3.1.2 Физические основы измельчения.

Измельчение осуществляется под действием внешних сил, преодолевающих силы взаимного сцепления частиц материала. При дроблении, куски твердого материала подвергаются объемной деформации, а затем, разрушаются по ослабленным дефектами сечениям с образованием новых поверхностей. Куски продукта дробления ослаблены трещинами значительно меньше исходных. Поэтому, с увеличением степени измельчения возрастает расход энергии.

Таким образом, работа, полезно затрачиваемая на дробление, расходуется на объемную деформацию разрушаемых кусков и на образование новых поверхностей.

Работа А_д упругого деформирования объема разрушаемого куска пропорциональна изменению объема (деформированному объему)

(1)

где - уменьшение объема кусков материала в результате их деформации перед разрушением;

Н_м - постоянная для данного материала, характеризующая его структурно-механические и физико-химические свойства.

Работа А_п - образованная новой поверхности при измельчении, пропорциональна ее изменению

(2)

где - приращение площади поверхности;

H_s - постоянная, характерная для данного материала и пропорциональная свободной поверхностной энергии твердого тела.

Полная работа внешних сил при дроблении выразится уравнением Ребиндера

(3)

Исходя из закона Гука, работу деформации А_д можно выразить уравнением

(4)

где - напряжение, Па;

Е - модуль упругости первого рода, Па, тогда уравнение (3) может быть записано в виде

(5)

Из уравнения (5) видно, что величина работы, затрачиваемой на разрушение материала, зависит от величины , т.е. от разрушающего напряжения и модуля упругости материала Е.

При грубом дроблении, когда величина вновь образованной поверхности невелика, второй член уравнения (3) не представляет значительной величины. Следовательно, можно записать

(6)

Это уравнение носит название уравнения Кирпичева-Кика.

Для случая тонкого измельчения в уравнении (3) можно пренебречь членом А_д и тогда уравнение примет вид

(7)

Это уравнение носит название уравнения Риттингера.

3.1.3 Крупное дробление. Определение угла захвата, числа качаний и производительности щековых дробилок.

Для крупного дробления применяют щековые и конусные дробилки, в которых, материал измельчается путем раздавливания в сочетании с раскалыванием или в результате сжатия и сдвига.

Конусные дробилки состоят из неподвижного и вращающегося конусов, а щековая – из неподвижной и качающейся щеки. С точки зрения теории процесса измельчения принцип работы этих дробилок, условно, можно считать одинаковым.

Различают щековые дробилки с верхним и нижним подвесом подвижной щеки. В первом случая качающаяся щека имеет наибольший размах вблизи места выхода дробленого продукта, ширина разгрузочного отверстия при этом переменна. Нижний подвес обеспечивает постоянную ширину разгрузочного отверстия, что гарантирует определенную максимальную крупность куска в дробленом продукте, но ограничивает производительность таких дробилок по сравнению с дробилками с верхним подвесом подвижной щеки.

Основные технологические характеристики щековых дробилок: угол захвата, скорость вращения коленчатого вала, обеспечивающего качание щеки, производительность и потребляемая мощность.

Угол между плоскостями щек при их максимальном сближении называется углом захвата. Если угол захвата очень велик, то куски материала могут выталкиваться из рабочего пространства дробилки. При недостаточном угле захвата достигается незначительная степень измельчения.

Рис.3.1.

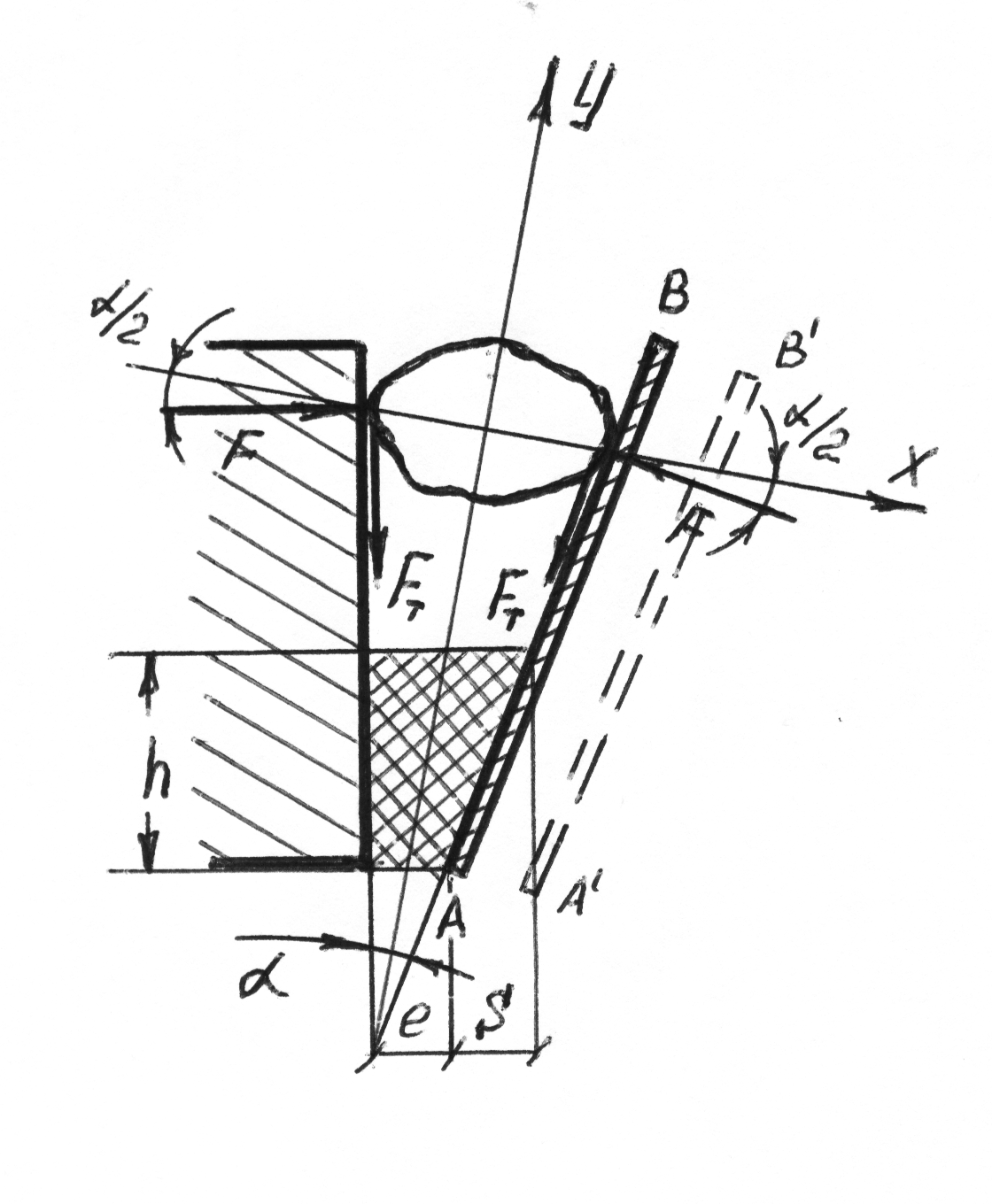
На кусок материала, раздавливаемый между щеками, действуют силы

и

Кусок материала не выталкивается вверх при условии, что равнодействующая от сил F направленная вверх по оси у, равна или меньше равнодействующей от сил трения т.е.

так как

,

то

откуда

Что является условием нормальной работы щековой дробилки.

Производительность щековой дробилки зависит от числа качаний подвижной щеки.

Принимая, что щека АВ совершает не качательное, а поступательное движение, что за каждый оборот коленчатого вала из дробилки под действием своего веса выпадает материал в объеме призмы, можно определить оптимальное число оборотов вала. Высота призмы h может быть выражена через ход щеки S и угол захвата .

(1)

При п оборотах вала в минуту время разгрузки материала (время холостого хода) составит

(2)

Путь свободного падения материала (за время ) равен высоте трапеции

или (3)

тогда

(4)

Число оборотов вала, рассчитанное по этому уравнению, является максимально допустимым. Практически принимают:

Теоретическую производительность дробилки можно определить, считая, что объем раздробленного материала, выпавшего за один ход щеки, равен объему призмы

где l – длина загрузочного отверстия дробилки;

Н – площадь трапеции.

Если е – минимальная ширина выпускной щели дробилки, то

При п ходах щеки в минуту, производительность составит

где коэффициент разрыхления материала на выходе.

3.1.4 Среднее и мелкое дробление. Определение минимально допустимого диаметра валков.

Для среднего и мелкого дробления используют ударно-центробежные (молотковые и дисковые дробилки, дезинтеграторы и дисмембраторы) и вальцевые дробилки.

Рабочей частью вальцевой дробилки являются горизонтальные валки. Количество валков может быть различным. Простейшая дробилка имеет один валок, вращающийся вокруг горизонтальной оси параллельно неподвижной рабочей щеке (деке). Однако чаще дробилки имеют пару или несколько пар валков. Парные валки вращаются навстречу друг другу, и дробление происходит между ними. По характеру поверхности валков они могут быть гладкими, рифлеными и зубчатыми.

При вращении валков, куски материала должны быть захвачены и раздроблены, для этого между диаметрами валков и размером куска должно выполняться определенное соотношение.

Определим минимально допустимый диаметр валков, необходимый для захвата измельчаемой частицы при горизонтальном расположении, одинаковой скорости валков и нулевой начальной скорости шарообразной измельчаемой частицы.

Рис.3.2.

Из рисунка видно, что частица диаметром d действует на валки в точках А по нормалям к касательным с некоторым усилием F. В свою очередь частица испытывает со стороны валков такие же усилия. Вертикальная составляющая этих сил R стремиться вытолкнуть частицу из сферического клина, образуемого цилиндрическими поверхностями валков, а вертикальная составляющая сил трения затягивает частицу в пространство между валками.

Для того чтобы частица была затянута валками, необходимо, чтобы соблюдалось условие

откуда

.

Следовательно, угол называемый углом захвата, должен быть меньше угла трения частицы о поверхность валка . Кроме того,

откуда

.

Минимально допустимый диаметр валков по условию захвата частицы будет

.

3.1.5 Тонкое измельчение. Определение критической частоты вращения шаровой мельницы.

Для тонкого и сверхтонкого измельчения применяют шаровые, стержневые, колойдные мельницы и стройные дробилки.

Шаровые мельницы состоят из вращающегося цилиндра, внутри которого находятся чугунные шары. При вращении корпуса мельницы, шары поднимаются на некоторую высоту, прижимаясь к корпусу центробежной силой, и падая, раскалывают материал, находящийся на поверхности, а материал, находящийся между шарами в это время интенсивно истирается. При достижении определенного размера, материал выводится из машины через отверстия решета.

При вращении цилиндра, шары и материал могут:

1. находится в состоянии относительного покоя (т.е. вращаться вместе с цилиндром).

2. совершать относительное движение

3. совершать свободное падение после отрыва от несущей поверхности.

Рис.3.3.

На частицу, находящуюся внутри цилиндра вращающегося с постоянной угловой скоростью, действуют:

Сила тяжести центробежная сила инерции нормальная реакция опоры N и сила трения

. (1)

. (2)

Частица, будет вращаться вместе с поверхностью цилиндра в том, случае, если, поднявшись на угол она не оторвется от поверхности цилиндра, т.е. будет выполняться условие

(3)

Скорость вращения, соответствующая равенству этих сил называется критической скоростью вращения.

учитывая, что

и

(4)

В большинстве случаев, число оборотов шаровых мельниц принимается равным 70-75% от критического числа оборотов.

Условно считаем, что частица, находящаяся в точке 1, положение которой определяется углом , начинается относительное движение частицы, а в точке 2, определяемой углом , происходит отрыв от поверхности цилиндра.

Условие начала относительного движения частицы определяется равенством движущих сил и сил, препятствующих этому движению т.е.

(5)

После сокращения на m и подстановки получим,

(6)

. (7)

, (8)

откуда

. (9)

Частоту вращения цилиндра, соответствующую началу скольжения частицы, можно определить из выражения (8).

(10)

(11)

Условие отрыва частицы от поверхности цилиндра определяется равенством нулю нормальной реакции опоры т.е

. (12)

а

(13)

При сравнении формул (9) и (13) видно, что может быть равен только в том случае, если что практически невозможно, всегда и т.е. относительное движение происходит всегда раньше, чем отрыв частицы.

Для определения момента отрыва частицы от поверхности цилиндра, часто пользуются уравнением (13). Для получения более точного результата, к ранее рассмотренной схеме сил, действующих на частицу, следует добавить силы инерции, возникающие при относительном движении частицы.

.

Рис.3.4.

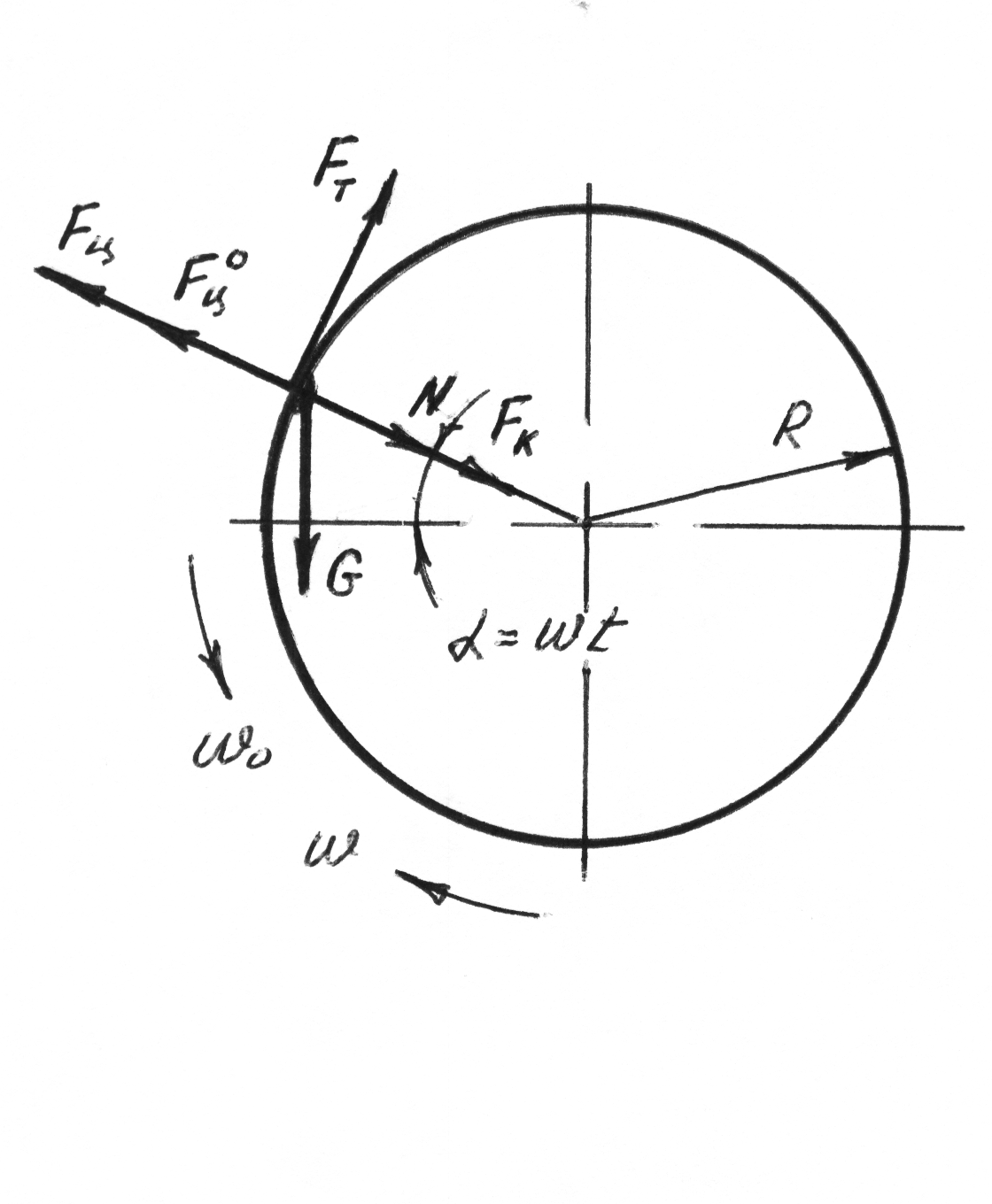
- угол, соответствующий перемещению частицы в относительном движении. Момент отрыва частицы от несущей поверхности будет иметь следующий вид:

(14)

откуда

, (15)

или

, (16)

и

. (17)

Решая уравнение (16) относительно , получим

(18)

Учитывая противоположные направления переносной и относительной угловых скоростей, запишем значение абсолютной угловой скорости частицы.

(19)

В формулах (18) и (19) верхние знаки будут соответствовать спуску частицы, нижние – подъему. Очевидно, что отрыв частицы может быть только при ее подъеме.