2.9 Осаждение под действием центробежной силы

Недостатками отстойников являются их большие размеры и незначительная (< 0,5 м/ч) скорость осаждения частиц. Они особенно малоэффективны при разделении смесей, частицы которые имеют размеры d_э < 5 мкм, или когда их плотность близка к плотности среды. Эффективное выделение таких частиц из суспензий и эмульсий достигается осаждением их в поле действия центробежной силы, которая в десятки раз превосходит силу тяжести.

При вращательном движении смеси на взвешенную частицу действует центробежная сила, отбрасывающая частицу от центра к периферии со скоростью, равной скорости осаждения.

Величина центробежной силы при этом

.

Для определения эффективности осаждения в центробежных устройствах сравним величину центробежной силы с силой тяжести, действующих на частицу.

Сила тяжести (без учета подъемной силы)

Приравняв эти силы, получим

,

т.е. центробежная сила больше силы тяжести в раз.

Величина называется фактором разделения или числом Фруда. Она показывает, во сколько раз действие центробежной силы превосходит действие силы тяжести. Чем больше фактор разделения, тем выше разделительная способность центробежных устройств.

При ламинарном режиме осаждения в центробежных устройствах скорость осаждения определяют по уравнению Стокса с учетом фактора разделения , т.е.

В процессе центробежного осаждения фактор разделения и скорость осаждения изменяются, так как они зависят от переменного радиуса R , на котором может находиться частица и осаждаться последовательно по трем режимам, а в частных случаях по двум или одному из них.

2.10 Основные закономерности осаждения в центробежном поле

Рассмотрим некоторые общие закономерности равновесия жидкости, находящейся во вращательном движении.

Рис. 2.6.

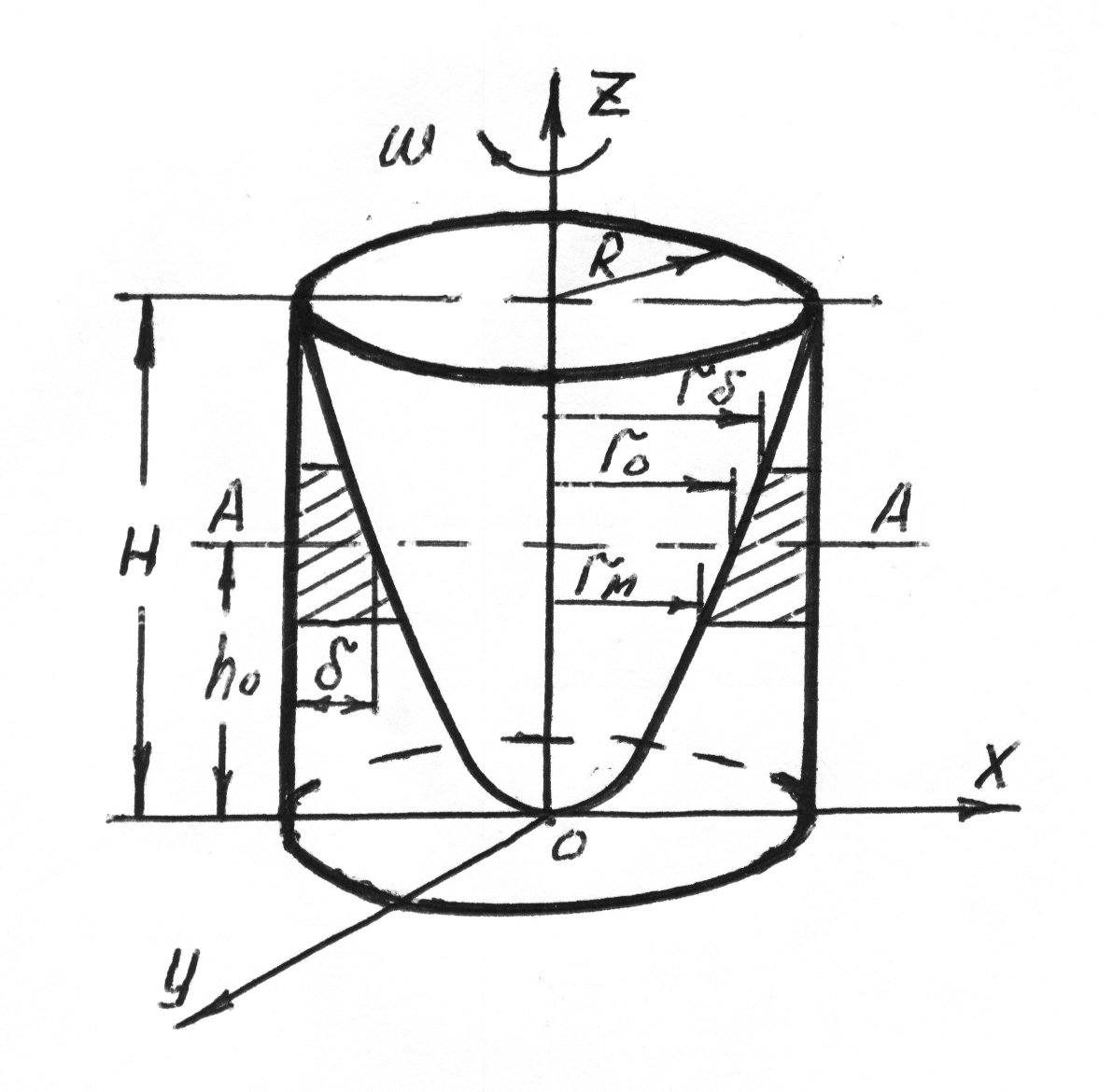
Предположим, что цилиндрический сосуд имеет внутренний радиус R и высоту H, он заполнен до уровня h_o какой-либо жидкостью. Если такой цилиндр вращать, то вследствие трения между жидкостью и стенками сосуда эта жидкость также начнет вращаться вместе с цилиндром, поднимаясь при этом у стенок и опускаясь в центре.

Высоту цилиндра H, первоначальный уровень h_o и конечную угловую скорость вращения подберем такими, чтобы жидкость поднялась до верхней кромки и опустилась до дна в центре. Если скорость вращения останется постоянной, то жидкость будет находиться в состоянии относительного покоя. Поэтому для установления закономерностей этого состояния можно применить дифференциальное уравнение гидростатики Эйлера, которое для данной системы запишем в следующем виде:

, (1)

где р - давление в любой точки жидкости;

- плотность жидкости;

x,y,z – проекция ускорений на координатные оси.

В данном случае на произвольно выбранную частицу жидкости М будет действовать центробежная сила, проекции ускорений которой на координатные оси будут:

, (2)

(3)

Кроме того, на эту частицу будет действовать сила тяжести, которая в соответствии с принятым направлением оси z выразится

(4)

Подставляя эти значения в уравнение (1) и интегрируя его, получим

(5)

Постоянную интегрирования найдем из условия, что при x=y=z=0 избыточное давление на поверхности жидкости равно нулю, следовательно и С = 0. Заменив текущие координаты х и у переменным радиусом вращения r по формуле

(6)

приходим к формуле

(7)

Из этой формулы видно, что свободной поверхностью является параболой вращения, высота подъема в котором пропорциональна квадратам угловой скорости и радиуса вращения и не зависит от физических параметров, то есть от рода жидкости.

Максимальная высота подъема будет, очевидно, при максимальном радиусе вращения r = R, то есть

(8)

Внутренняя поверхность вращения жидкости в барабане центрифуги представляет собой часть параболоида вращения, вырезанную двумя горизонтальными плоскостями с разными по величине внутренними радиусами: вверху – с большим радиусом r_б и внизу – с меньшим радиусом r_м.

Покажем, что разница между этими радиусами практически очень мала.

Объем жидкости в цилиндре до его вращения можно представить так

(9)

Объем параболоида вращения найдем по формуле

(10)

Продифференцировав выражение (7)

(11)

Подставляем его в (10) и интегрируя получим

(12)

Объем жидкости в цилиндре остается неизменным, поэтому объем всего сосуда

(13)

должен быть равен сумме объемов жидкости и пустого параболоида

(14)

На основании этого равенства объема получаем

(15)

Сокращая обе части этого уравнения на и подставляя вместо Н его значение из формулы (8), получаем

(16)

Сравнивая выражения (8) и (16), приходим к выводу, что

(17)

т.е. горизонтальная плоскость жидкости в покоящемся цилиндре делит на две равные части высоту параболоида во вращающемся цилиндре, форму которого жидкость принимает. Отсюда следует, что в барабане центрифуги жидкость при данном ее объеме и скорости вращения опускается и поднимается вверх на одинаковое расстояние от плоскости, делящей высоту барабана пополам.

Если высота барабана h, то на основании вышеизложенного и в соответствии с формулой (7) имеем

, (18)

(19)

Сравнивая последние формулы нетрудно заметить, что разница r_б – r_м очень мала, и тем меньше, чем больше скорость вращения цилиндра. Поэтому практически внутреннюю поверхность части параболоида вращения считаем цилиндрической со средним радиусом

(20)

В этом случае толщина слоя жидкости в барабане

(21)

Давление центрифугирования Р в средней плоскости параболоида А-А обусловливается разностью высот столбов жидкости Н – h_о. Умножив правые части выражений (7) и (8) на удельный вес и вычитая почленно, получим

(22)

Причем, здесь принято выражение r = r_o, соответствующее высоте h = h_o. В барабане центрифуги давление на днище будет на величину больше, а на верхнее ограничительное кольцо на ту же величину меньше, чем в средней плоскости, в соответствии с формулой (22).

Разложив разность квадратов радиусов на сумму и разность, и принимая во внимание, что сумма

(23)

является средним радиусом кольцевого сечения слоя жидкости, а разница в соответствии с формулой (21) толщиной этого кольца , формулу (22) можем записать в виде

(24)

Но величина представляет собой фактор разделения для среднего радиуса. Поэтому, мы можем записать, что

(25)

Гидростатическое давление столба жидкости высотой, равной высоте слоя жидкости над фильтрующим слоем

,

представляет собой гидростатическое давление столба жидкости высотой, равной толщине слоя в барабане центрифуги. Следовательно, при центрифугировании давление увеличивается по сравнению с гидростатическим в гравитационном поле пропорционально фактору разделения.

Схемы, устройство и принцип действия осадительных центрифуг и гидроциклонов. ( самостоятельно)