80. Колебательные движения материальной точки. Свободные и вынужденные колебания. Затухающие колебания. Решение примера.

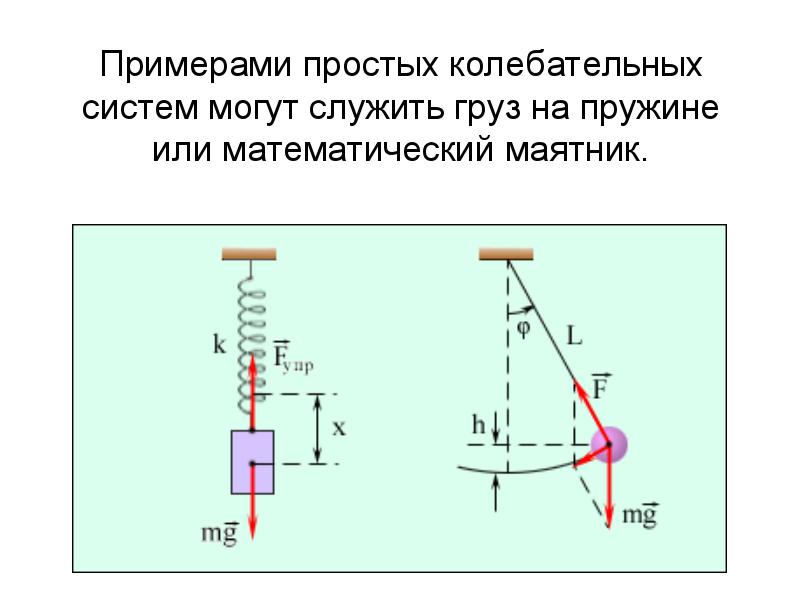
Колебательные движения тела – это движения, повторяющиеся через определенный промежуток времени.

Амплитуда – это наибольшее отклонение колеблющегося тела от положения равновесия.

Измеряется в метрах, сантиметрах и т.п.

Период колебаний – это промежуток времени, в течение которого тело совершает одно полное колебание.

Частота колебаний – это число колебаний, совершаемых в единицу времени.

Гармонические колебания — колебания, при которых колеблющаяся величина    изменяется со временем по закону синуса или косинуса: , где  — амплитуда колебаний,  — фаза,  — начальная фаза в момент  ,  — круговая (циклическая) частота.

Период колебаний — время, за которое колебание совершает полный цикл. За период фаза гармонических колебаний изменяется на  : . Частота колебаний — число полных колебаний, совершаемых за единицу времени. Частота колебаний   измеряется в Герцах [Гц]. .

Гармонические колебания возникают, когда сила, возвращающая тело в положение равновесия, пропорциональна величине отклонения от равновесия. В этом случае уравнение динамики принимает вид однородного дифференциального уравнения второго порядка, решением которого является гармоническая функция (синуса или косинуса): .

При наличии сил трения или сопротивления среды свободные механические колебания становятся затухающими. Если сила трения пропорциональна скорости движения тела, то есть , дифференциальное уравнение колебаний пружинного маятника принимает вид: , или , где   — коэффициент затухания,  — частота незатухающих колебаний.

Решение уравнения: , где   — частота затухающих колебаний,  — амплитуда затухающих колебаний.

Декремент затухания — отношению амплитуд затухающих колебаний, соответствующим моментам времени, отличающимся на период: .

Время релаксации — промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в   раз: .

Логарифмический декремент затухания: , где  — число колебаний, совершаемых за время релаксации.

Добротность колебательной системы: . При малых затуханиях ( ) энергия колебаний пропорциональна квадрату амплитуды и изменяется по закону: . ,  где ( ) — убыль энергии за один период колебаний. Таким образом, добротность, деленная на  , равна отношению энергии, запасенной в колебательной системе, к убыли этой энергии за один период колебаний.

Пример

Условие задачи:

Некоторая точка движется вдоль оси x по закону x = a sin² (ωt - π/4). Найти:  а) амплитуду и период колебаний; изобразить график x (t);  б) проекцию скорости v_x как функцию координаты x; изобразить график v_x (x).