76. Законы механики Галилея-Ньютона. Момент силы относительно точки и оси. Решение примера.

1 Закон (закон инерции)

Изолированная материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока не будет выведена из него действием других тел.

Свойство точки сохранять состояние покоя или равномерного прямолинейного движения называется свойством инерции.

Системы отсчета, в которых выполняется 1 закон Ньютона называются инерциальными.

2 Закон (основной закон динамики точки)

Ускорение свободной материальной точки под действием силы пропорционально силе и обратно пропорционально массе точки:

;

. (1)

Уравнение (1) называют основным уравнением динамики точки и справедливо в случае m=const.

Из уравнения видно, что масса материальной частицы является мерой инерции.

2 закон Ньютона можно распространить на движение несвободной материальной точки, пользуясь аксиомой освобождаемости связей, т.е. следует мат. Точку сделать свободной, отбросив связи и заменив их действие реакциями.

3 Закон (о действии и противодействии)

Силы взаимодействия между двумя материальными частицами равны по модулю и направлены по одной прямой в противоположные стороны.

4 Закон (закон независимости действия сил)

Ускорение свободной материальной точки под действием системы сил } равно векторной сумме ускорений, приобретенных точкой под действием каждой из сил }.

,

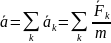где – равнодействующая всех сил, приложенных к частице.

Система отсчета, неподвижная относительно поверхности Земли, во многих технических задачах может приближенно считаться инерциальной. Ближайшая к нам инерциальная система отсчета – барицентрическая система отсчета, связанная с центром масс Солнечной системы, оси которой направлены на неподвижные звезды.

Момент силы относительно точки

Момент силы относительно центра равен взятому со знаком «+» или «-» произведению модуля силы на ее плечо относительно данного центра.

Плечом силы F относительно центра А называется длина перпендикуляра, опущенного из точки А на линию действия силы. Знак момента плюс, если поворот тела под действием силы F вокруг точки А виден в направлении против хода часовой стрелки.

Момент силы относительно центра ка вектор равен векторному произведению радиуса вектора точки приложения силы относительно данного центра на вектор силы.

где D – точка приложения силы F.

Вектор момента направлен перпендикулярно плоскости моментного треугольника в ту сторону, откуда поворот тела вокруг точки А под действием силы F виден в направлении против хода часовой стрелки.

Момент силы относительно оси

Момент силы относительно оси Z равен взятому со знаком «+» или «-» произведению модуля проекции силы на плоскость α, перпендикулярную оси, на плечо этой проекции относительно точки А пересечения оси Z c плоскостью α.

Знак момента плюс, если с положительного конца оси поворот виден против часовой стрелки.

Связь между моментами силы относительно центра и оси:

Пример Условие задачи

К вершинам квадрата ABCD (AB=AD=2 м), расположенного в горизонтальной плоскости, приложены силы P₁, P₂, P₃ и P₄, как показано на рис. 159. Сила P₁ направлена по диагонали АС; сила P₂ действует вверх перпендикулярно к плоскости квадрата; сила P₃ действует в плоскости квадрата, и ее направление образует с диагональю СА угол α=20°; сила P₄ действует в плоскости, перпендикулярной к плоскости квадрата, и направлена к стороне DC под углом β=30°. Определить моменты каждой силы относительно осей х, у и z.

Модули сил P₁ = P₂ = P₃ = P₄ = 5 кн.

Решение: