20.Угол между плоскостями. Условие параллельности и перпендикулярности плоскостей

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами n1 и n2 плоскостей α1 и α2 равен одному из указанных смежных двугранных углов 

Поэтому 

Т.к.

n₁=(A₁,B₁,C₁)

n₂=(A₂,B₂,C₂)

то

Условие параллельности двух плоскостей.

Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы n1 и n2 параллельны, а значит

И так, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, n1*n2 = 0 или A1A2 + B1B2 + C1C2 = 0

Таким образом,

22.Нормированное уравнение плоскости.

Где:

-углы, образуемые нормальным вектором плоскости с осями координат; p- расстояние от начала координат до плоскости.

Приведение общего уравнения плоскости к нормальному виду:

Здесь

нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если произвольно, если D = 0 .

23.Прямая в пространстве. Общее уравнение прямой

Прямая в пространстве может быть задана также как пересечение двух плоскостей, если плоскости не параллельны:

Все формы задания прямой в пространстве взаимосвязаны.

24.Параметрическое и Каноническое уравнение прямой.

Параметрическое:

Векторное уравнение (13.2) в координатной форме представляется следующим образом

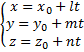
Каноническое:

Исключив t из уравнения (13.3), разрешив их сначала относительно t, а затем, приравняв правые части равенств, имеем:

Если какая – либо координата направляющего вектора равна нулю, то равен нулю и числитель дроби.

26.Угол между прямыми в пространстве. Условия параллельности и перпендикулярности двух прямых.

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами   и  . Так как  , то по формуле для косинуса угла между векторами получим

.

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов   и  :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l₁ параллельна l₂ тогда и только тогда, когда   параллелен  .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:  .

28 Условие принадлежности двух прямых одной плоскости

|	x-x1	y-y1	z-z1	|
|	l1	m1	n1	|	= 0
|	l2	m2	n2	|

Если это условие выполняется, прямые или параллельны или пересекаются

41 Координаты вектора в данном базисе

Определение. Базисом в пространстве Rⁿ называется любая система из n-линейно независимых векторов. Каждый вектор из Rⁿ, не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.      Пусть   – базис пространства Rⁿ и  . Тогда найдутся такие числа λ₁, λ₂, …, λ_n, что  .      Коэффициенты разложения λ₁, λ₂, …, λ_n, называются координатами вектора   в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.

Пример. Разложить вектор   по базису  .      Решение.  . Подставим координаты всех векторов и выполним действия над ними:            Приравняв координаты, получим систему уравнений:            Решим ее:  .      Таким образом, получим разложение:  .      В базисе   вектор   имеет координаты  .

46 Кольцо линейных преобразований Обратное преобразование

Линейные преобразования образуют кольцо линейх преобразований .Между кольцом матриц и кольцом линейных преобразований существует взаимно-однозначное соответствие.Сохраняет свои свойства при сложении и умножении на скаляр.

Матрица обратного преобразования является матрицей обратная исходной.

ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ

ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ

-отображение векторного пространства в себя, при к-ром образом суммы двух векторов является сумма их образов, а образом произведения вектора на число - произведение образа вектора на это число. Если V - векторное пространство, f - заданное в нем Л. п. и x, у - любые векторы пространства,   - любое число (элемент поля), то 

Кольцо - совокупность элементов, для которых определены операции сложения, вычитания и умножения, обладающие обычными свойствами операций над числами. Напр., кольцо целых чисел.