
Тест №3 Чебанов
.docТест №3
1
-
Двойным интегралом от функции (x,y) , непрерывной в замкнутой области GR2 , называется предел последовательности интегральных сумм Si при maxdiam
 Si0,
причём предел не зависит ни от способа
деления области G
на элементарные области
Si0,
причём предел не зависит ни от способа
деления области G
на элементарные области
 ,
ни от выбора точки M
внутри области
,
ни от выбора точки M
внутри области

-
С помощью двойного интеграла объём тела V={(x,y,z):f(x,y)<=z<=0,(x,y)G} записывается в виде: V=

-
Если функция (x,y), ((x,y)G) – плотность распределения масс, то физический смысл интеграла
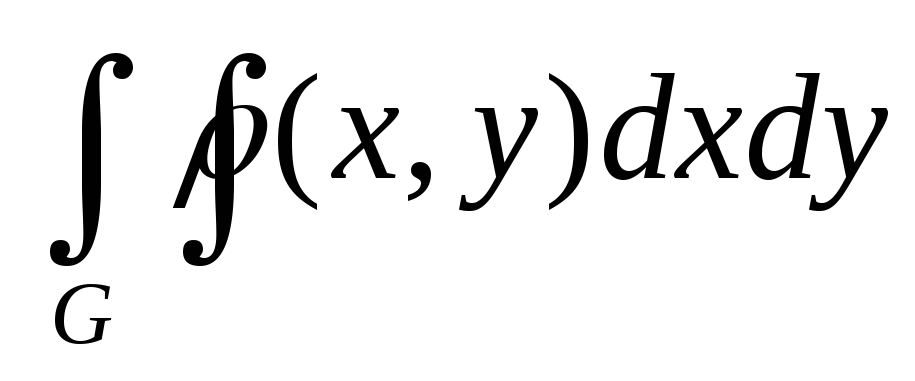 есть масса пластинки G.
есть масса пластинки G. -
Геометрический смысл интеграла
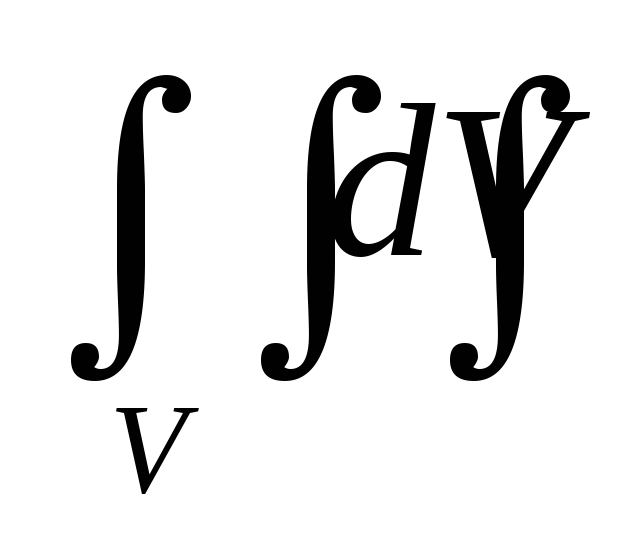 есть
объём области V
есть
объём области V
-
Интеграл
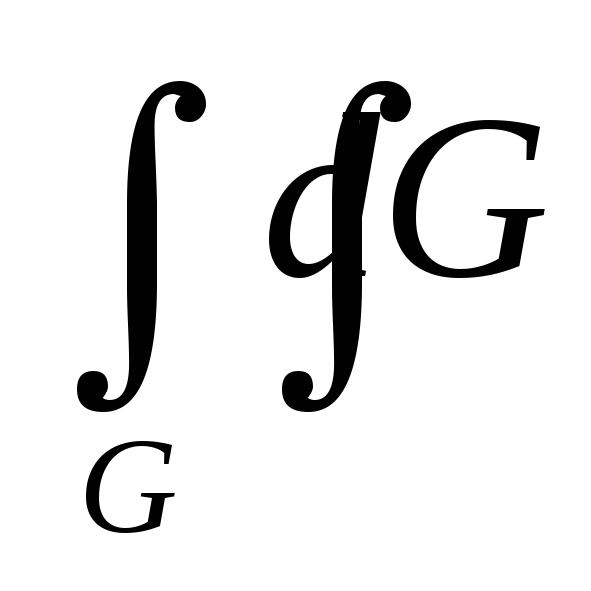 равен
площади области G.
равен
площади области G. -
Тройным интегралом от функции f(x,y,z), непрерывной в замкнутой области V, называется предел последовательности соответствующих интегральных сумм при max diam
 Vi0,
если этот предел не зависит ни от
способа деления области V,
ни от выбора точек Mi:
Vi0,
если этот предел не зависит ни от
способа деления области V,
ни от выбора точек Mi:
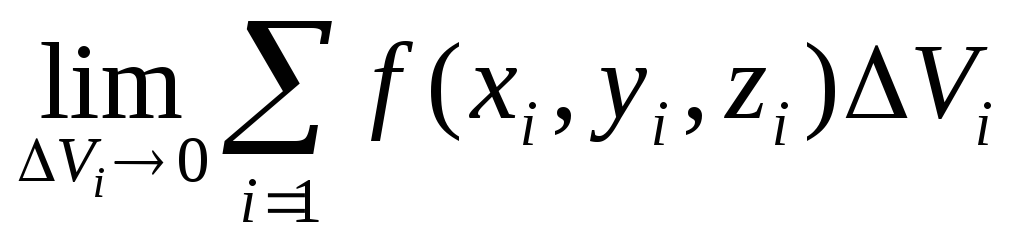

-
Если f(x,y) – неотрицательная интегрируемая функция в области G, то геометрический смысл
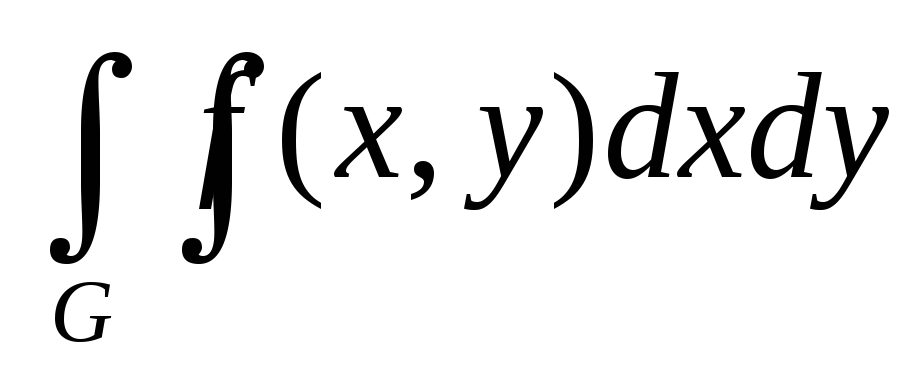 есть объём цилиндрического тела с
основанием G
,с образующими // оси OZ
и ограниченной сверху поверхностью
z=(x,y)
есть объём цилиндрического тела с
основанием G
,с образующими // оси OZ
и ограниченной сверху поверхностью
z=(x,y) -
Если функция (x,y,z), (x,y,z)V - плотность распределения масс, то физический смысл интеграла
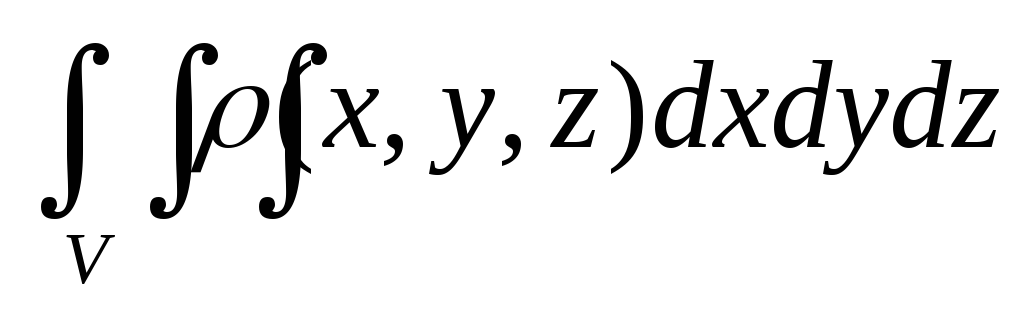 есть масса неоднородного тела сс
плотностью (x,y,z)
в каждой точке
есть масса неоднородного тела сс
плотностью (x,y,z)
в каждой точке -
Масса пластинки G R2 с плотностью (x,y), (x,y)G равна
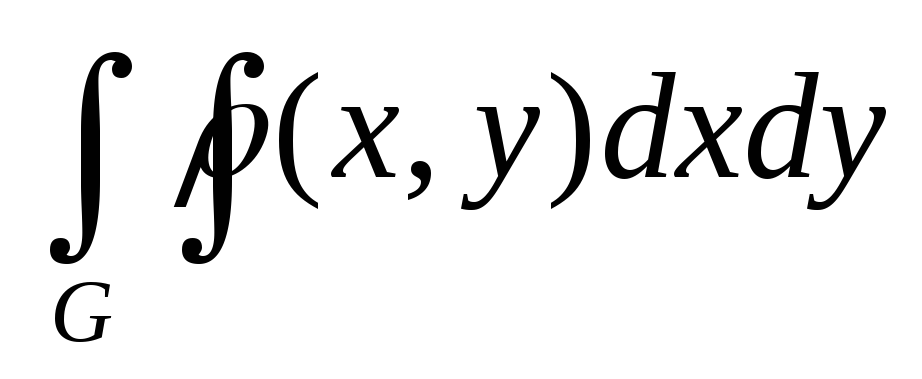
-
Площадь области G XOY равна
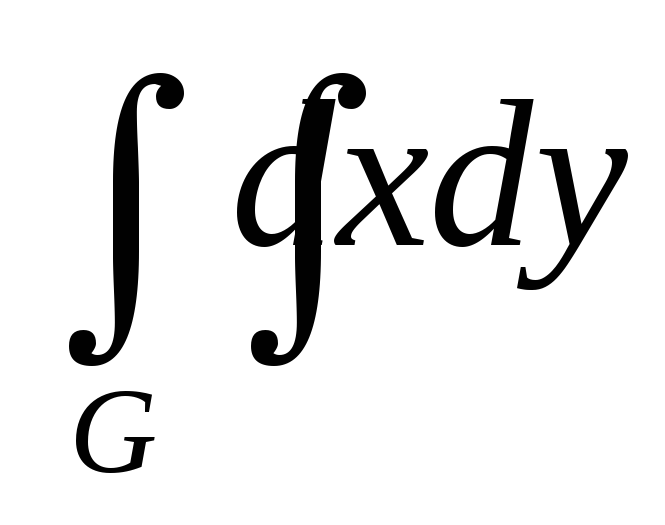
2
-
Если функции f(x,y) и g(x,y) интегрируемы на G, f(x,y) <= g(x,y) на G и
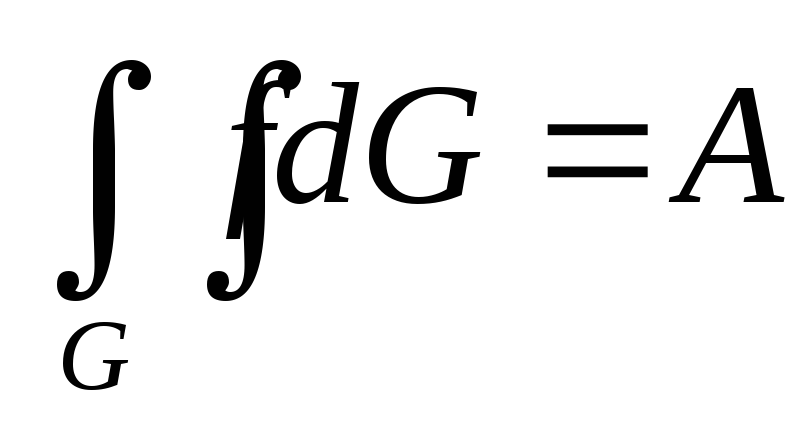 ,
а
,
а
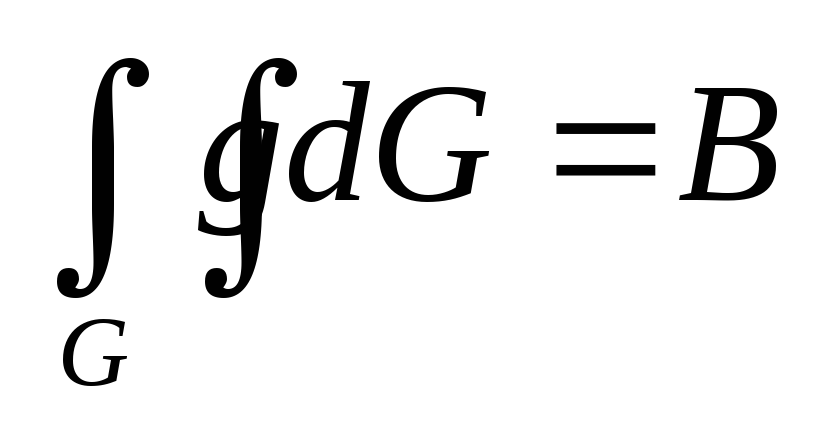 ,
то A
B
,
то A
B -
По теореме о сведении двойного интеграла к повторному, если функция (x,y) интегрируема на G, где G={(x,y):
 ,
a<=x<=b},
то
,
a<=x<=b},
то
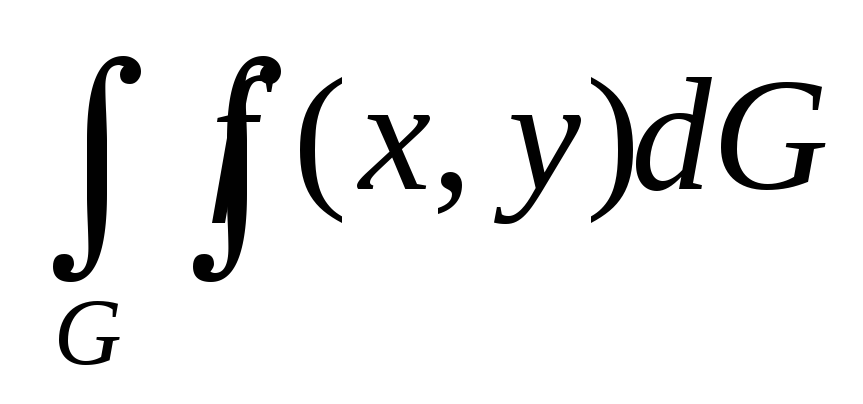 равен
равен
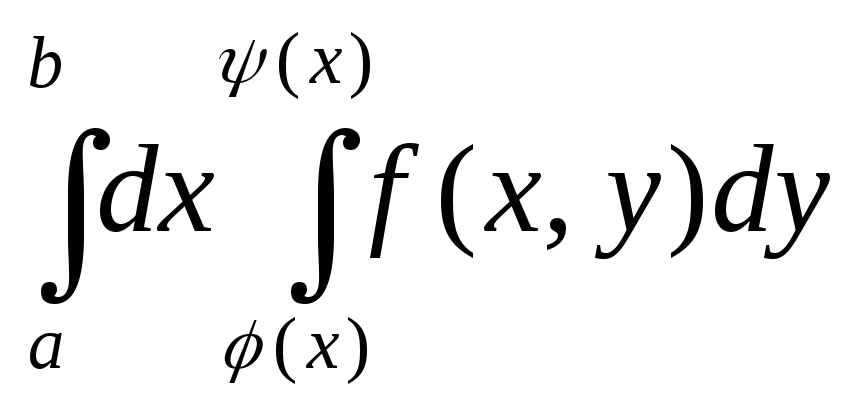
-
По свойству линейности, если функции f(x,y) и g(x,y) интегрируемы на G, тогда для любых чисел A и B сумма
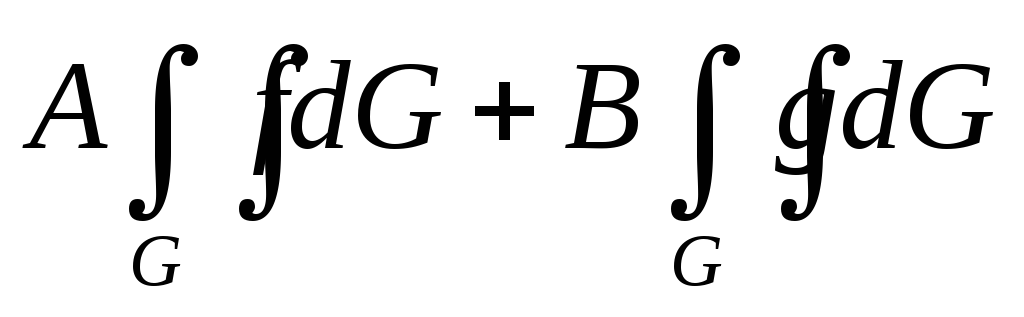 равна
равна
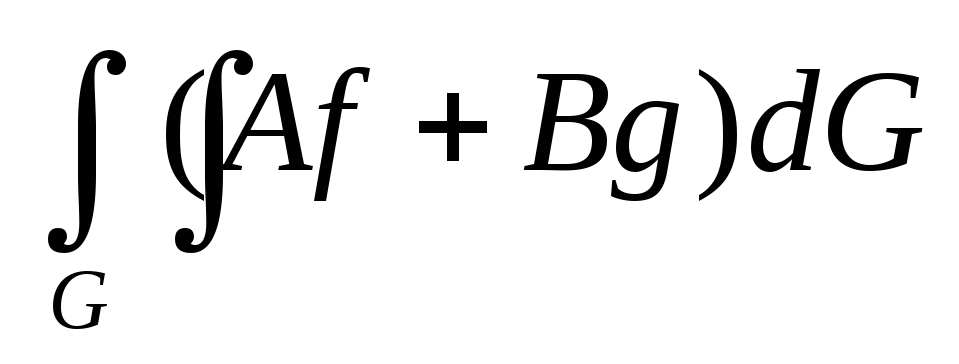
-
По свойству аддитивности , если области G, G1 и G2 такие, что G1 G, G2 =G|
 ,
а функция интегрируема на G,
то интегрируемый на G1
и G2
причём
,
а функция интегрируема на G,
то интегрируемый на G1
и G2
причём
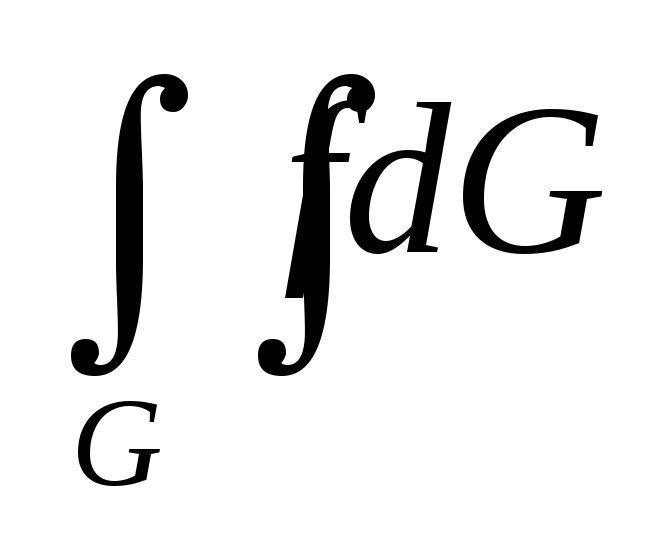 равен
равен
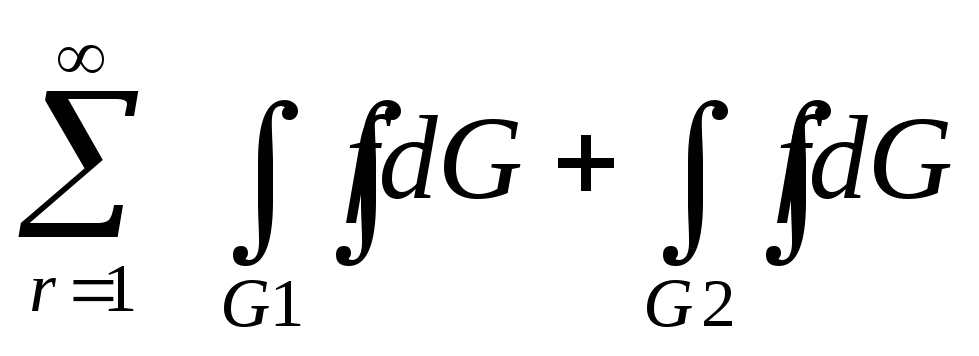
-
По свойству линейности, если функции f(x,y,z) и g(x,y,z) – интегрируемы на V, тогда для любых чисел A и B интеграл
 равен
равен
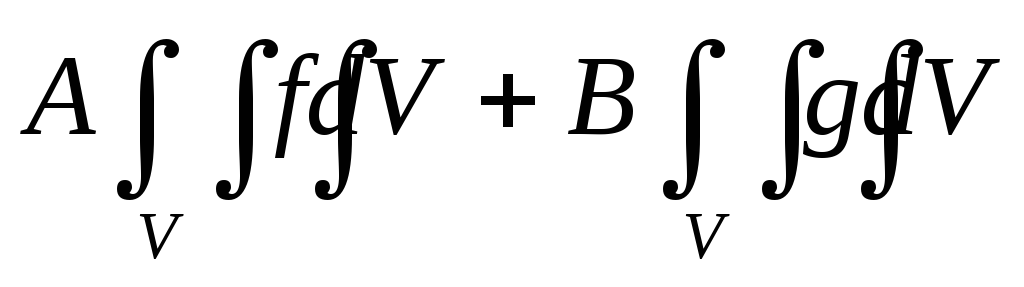
-
По свойству монотонности тройного интеграла, если функция f(x,y,z) неотрицательна и интегрируема на G, то выполняется неравенство
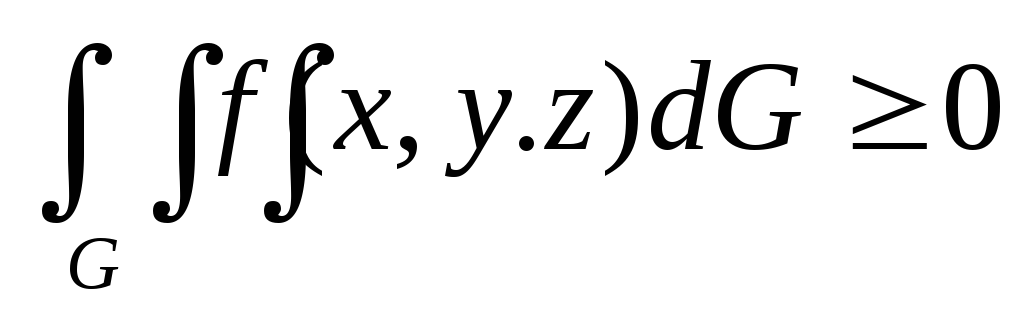
-
По свойству монотонности двойного интеграла, если функции f(x,y) и g(x,y) интегрируемы на G и f(x,y) <= g(x,y) на G, то

-
По свойству аддитивности, если области G, G1 и G2 такие, что G1 G, G2 =G|
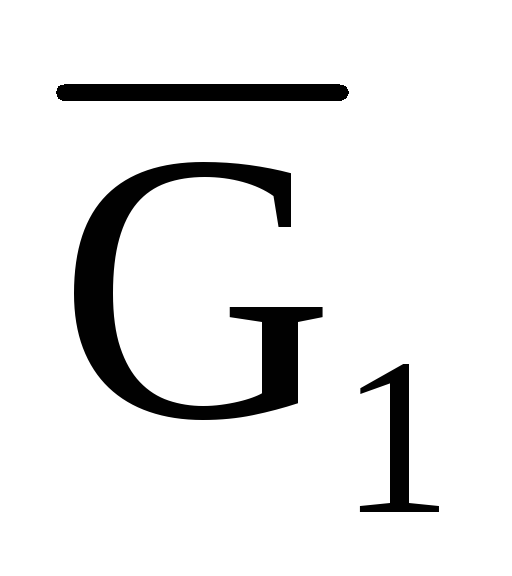 функция
(х,у)
- интегрируема в G,
то (x,y)
интегрируема на G1
и G2,
причем сумма равна
функция
(х,у)
- интегрируема в G,
то (x,y)
интегрируема на G1
и G2,
причем сумма равна
 равна
равна
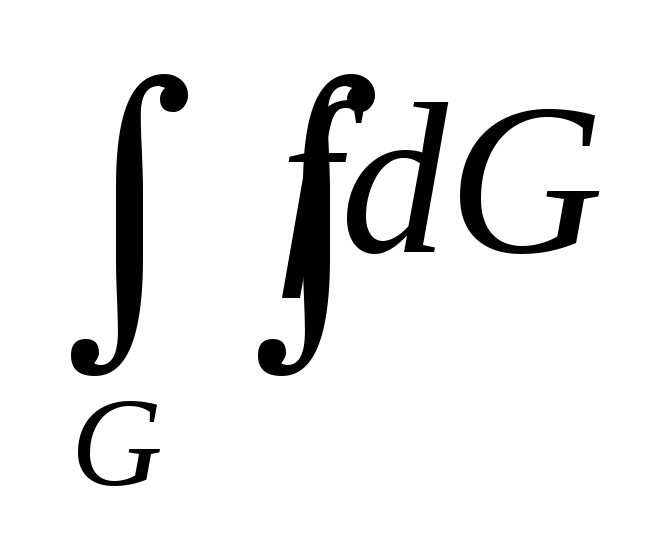
-
По свойству об оценке двойного интеграла, если f(x,y) интегрируема на G и m f M (m,M-const), то выполняется неравенство

-
По свойству двойного интеграла, если f(x,y) и |f(x,y)| интегрируемы на G, то для
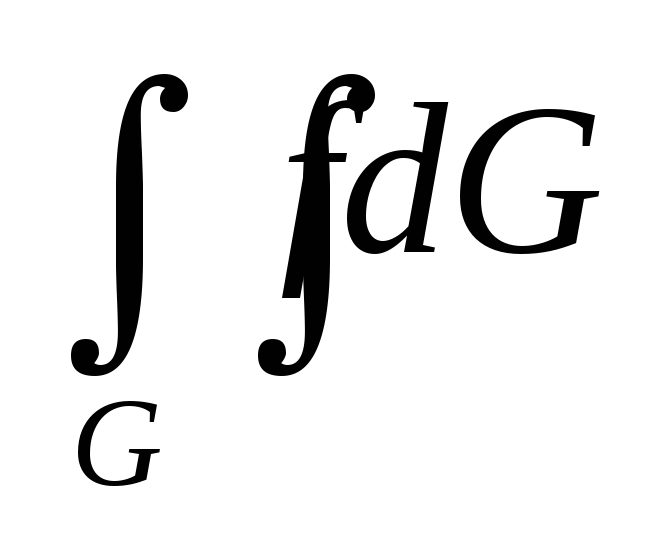 и
и
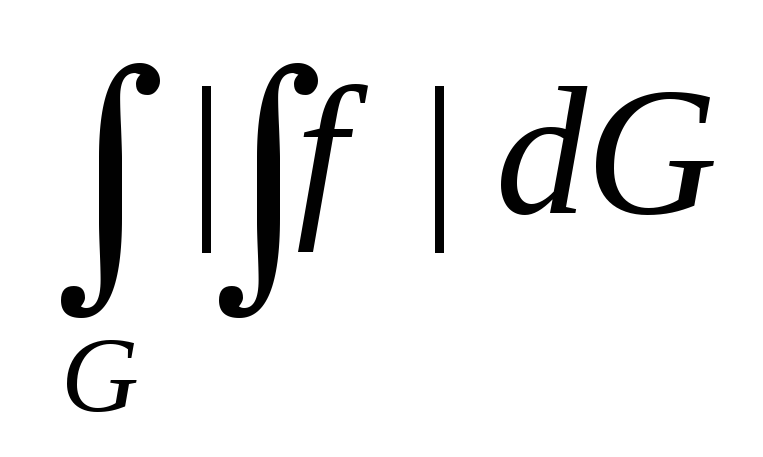 выполняется неравенство
выполняется неравенство

3
-
По свойству линейности, если функции f(x,y,z) и g(x,y,z) интегрируемы на V, то для любых чисел A и В интеграл v(A+Bg)dV равен AvdV+BvgdV
-
По свойству аддитивности, если области V, V1 и V2 такие, что V1V, V2=V\V1 и функция (x,y,z) интегрируема на V , то интеграл на V1 и V2 причём V(x,y,z)dV равен V1(x,y,z)dV+V2(x,y,z)dV
-
По свойству монотонности тройного интеграла, если функции (x,y,z) и g(x,y,z) интегрируемы на V и (x,y,z)g(x,y,z) на V, то V(x,y,z)dVVg(x,y,z)dV
-
По свойству тройного интеграла, если (x,y,z) и |(x,y,z)| интегрируемы на V ,то для |VdV| и V||dV выполняется неравенство |VdV|V||dV
-
По свойству об оценке тройного интеграла, если (x,y,z) интегрируема на V и mM (m,M -- const) , то выполняется неравенство VmdVV(x,y,z)dVVMdV
-
По свойству линейности, если функции (x,y,z) и g(x,y,z) интегрируемы на V, тогда для любых чисел A и B сумма AVdV+BVgdV равна V(A+Bg)dV
-
По теореме о сведение тройного интеграла к повторному, если функция (x,y,z) интегрируема на V , где V={(x,y,z):(x,y)z(x,y), (x,y)G} (G – проекция V) , то интеграл V(x,y,z)dV равен Gdxdy(x,y)(x,y)(x,y,z)dz
-
По свойству монотонности для тройного интеграла, если функция (x,y,z) – неотрицательна и интегрируема на VR3 , то выполняется неравенство V(x,y,z)dV0
-
По свойству аддитивности, если области V, V1 и V2 такие, что V1V, V2=V\V1 и функция (x,y,z) интегрируема на V , то интегрируема на V1 и V2 причём сумма V1dV+ V2dV равна VdV
-
Если функции (x,y,z) и g(x,y,z) интегрируемы на V и (x,y,z)g(x,y,z) на V и A=V(x,y,z)dV, B=Vg(x,y,z)dV, то справедливо соотношение: AB
4
-
Если формулы x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) задают взаимно однозначное, непрерывно дифференцируемое отображение области Т пространства переменных (u,v,w) на область пространства переменных (x,y,z), то якобиан отображения l(u,v,w) равен
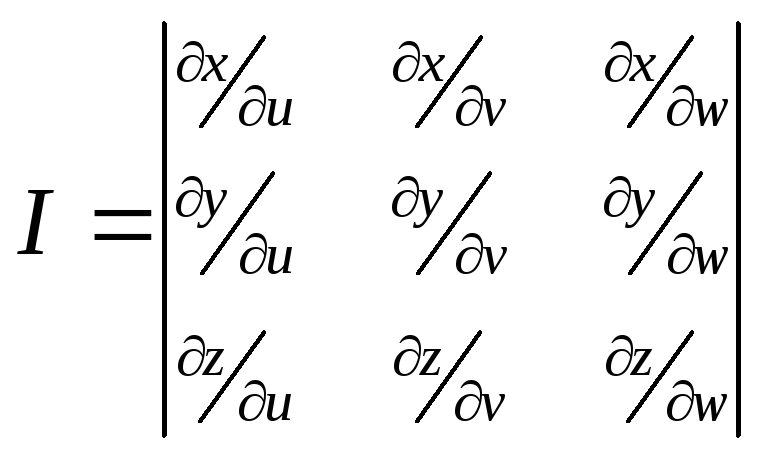
-
Если отображение области D плоскости переменных (r,) на область G плоскости переменных (x,y) определяется полярными координатами r и , то G(x,y)dxdy= D(rcos,rsin)rdrd
-
Якобиан J(r,,) отображения, определяемого сферическими координатами r,,, равен определителю
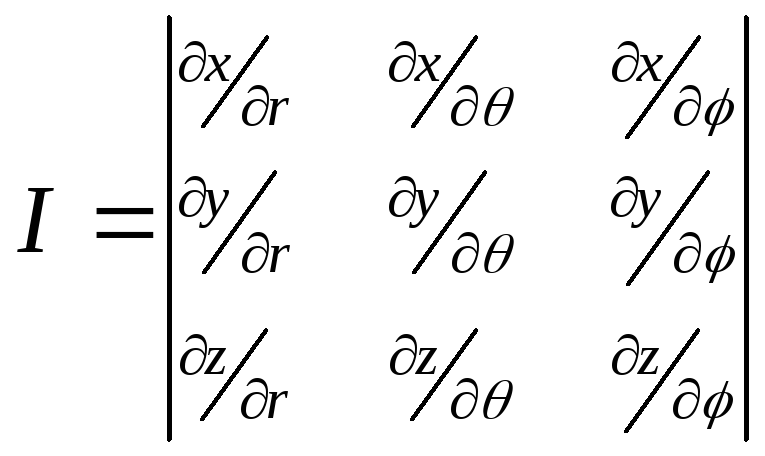
-
Если формулы x=x(u,v), y=y(u,v) задают взаимно однозначное и непрерывно дифференцируемое отображение области D плоскости переменных (u,v) на область G плоскости переменных (x,y) , то G(x,y)dxdy= D(x(u,v), y(u,v))Idudv где якобиан I(u,v) равен

-
Якобиан J(r,, z) отображения, определяемого цилиндрическими координатами r,, z, равен определителю
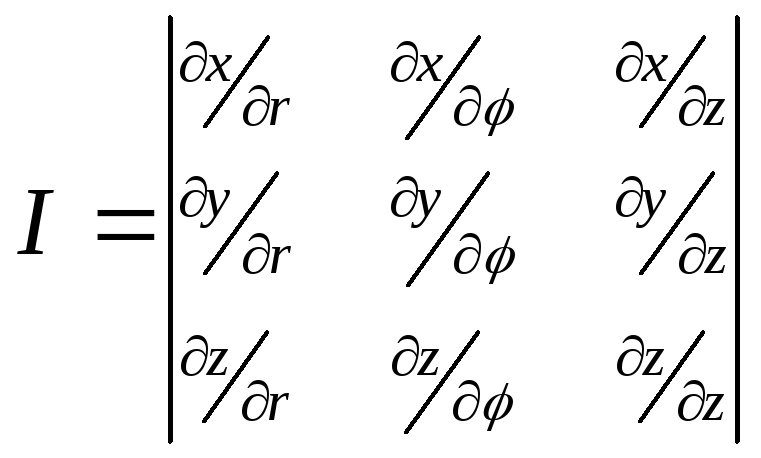
-
Если формулы x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) задают взаимно однозначное и непрерывно дифференцируемое отображение области Т пространства переменных (u,v,w) на область пространства переменных (x.y,z), то dxdydz=T(x,y,z)Idudvdw , где якобиан I(u,v,w) равен

-
Если отображение области Т пространства переменных (r,,) на область пространства переменных (x,y,z) определяется сферическими координатами, то dxdydz=T(rsincos, rsinsin ,rcos)Idrdd
-
Если формулы x=x(u,v), у=y(u.v) задают взаимно однозначное и непрерывно дифференцируемое отображение области D плоскости переменных (u,v) на область G плоскости переменных (х,у). то якобиан I(u,v) отображения равен
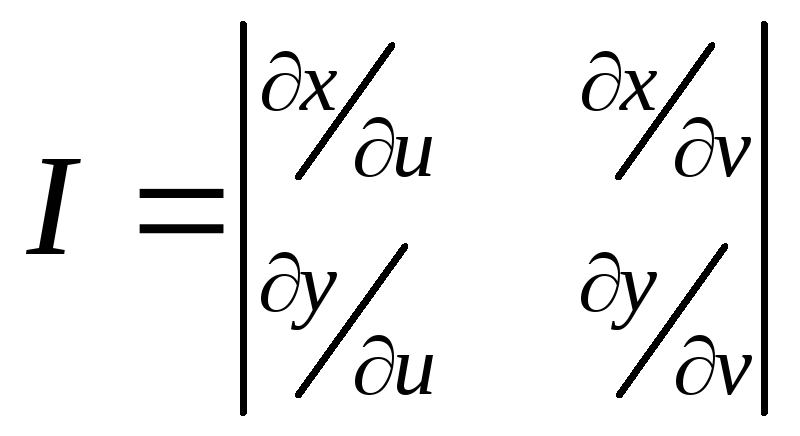
-
Если отображение области Т пространства переменных (r, , z) на область пространства переменных (x, y, z) определяется цилиндрическими координатами, то (x,y,z)dxdydz=T(rcos, rsin, z)rdrddz
-
Если функции x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) задают взаимно однозначное и непрерывно дифференцируемое отображение области Т пространства переменных (u,v,w) на область пространства переменных (x,y,z), и якобиан отображения I(u.v.w) равен
 ,
то (x,y,z)dxdydz=T(x(u.v.w),
y(u.v.w),
z(u.v.w))Idudvdw
,
то (x,y,z)dxdydz=T(x(u.v.w),
y(u.v.w),
z(u.v.w))Idudvdw
5
-
Если функция (x,y) – неотрицательна и интегрируема в области G , то геометрический смысл интеграла G(x,y)dxdy есть объём тела Q, ограниченного поверхностью , образующие которой параллельны оси OZ , а направляющей служит граница области G
-
Статический момент MOX относительно оси OX пластинки G, с плотностью (x,y), (x,y)G, равен MOX=Gy(x,y)dxdy
-
Геометрический смысл Gdxdy есть площадь плоской фигуры , занимающей область G
-
Статический момент MOY относительно оси OY пластинки G с плотностью (x,y), ((x,y)G) равен MOY=Gx(x,y)dxdy
-
Абсцисса центра тяжести
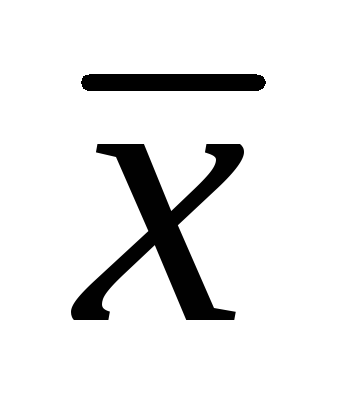 пластинки
GR2
с заданной плотностью (x,y)
, ((x,y)G)
равна
пластинки
GR2
с заданной плотностью (x,y)
, ((x,y)G)
равна
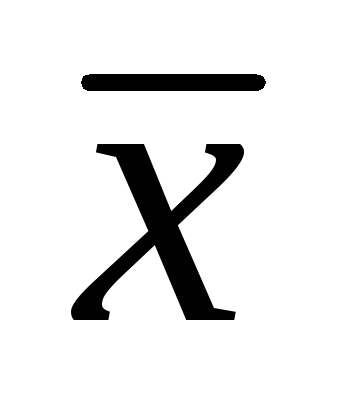 =My
/
M=(Gx(x,y)dxdy)
/ (G(x,y)dxdy)
=My
/
M=(Gx(x,y)dxdy)
/ (G(x,y)dxdy) -
Моменты инерции IX , IY пластинки GR2 с плотностью (x,y) , ((x,y)G) равны IX=Gy2(x,y)dxdy, IY=Gx2(x,y)dxdy
-
Если (x,y) , (x,y)G, - плотность распределения масс, то механический смысл интеграла Gx(x,y)dxdy есть статический момент пластинки
-
Момент инерции IO относительно начала координат пластинки GR2 с плотностью (х,у), (x,y)G, равен IO=G(x2+y2)(x,y)dxdy
-
Согласно геометрическому смыслу двойного интеграла объем замкнутой области V={(x,y,z):(x,y)G, (x,y) z (x,y)}, где функции и интегрируемы в G, равен G((x,y)+(x,y))(x,y)dxdy
-
Если (х,у), ((x,y)G) - плотность распределения масс, то механический смысл интеграла Gy2(x,y)dxdy есть момент инерции пластинки
6
-
По определению криволинейным интегралом первого рода от функции f(x,y), непрерывной на кусочно-гладкой кривой АВ, называется предел последовательности интегральных сумм i при max i0 , который не зависит ни от способа деления дуги (AB) точками А i , ни от выбора точек М i в частичных дугах А i-1 А i , его обозначение limmaxi0 i=1(xi, yi) i =(AB)(x,y)d
-
Согласно геометрическому смыслу тройного интеграла, объем области V R2 вычисляется по формуле V=Vdxdydz
-
Статический момент МXY относительно плоскости XOY тела V R3 с плотностью (х, у, z), (x,y,z )V равен МXY=Vz(x,y,z)dxdydz
-
Абсцисса
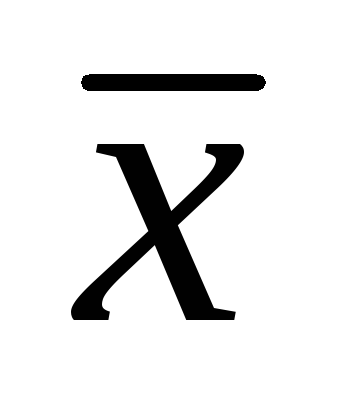 центра тяжести тела V
R3
с плотностью (х,
у, z), (х. у, z)
V
равна
центра тяжести тела V
R3
с плотностью (х,
у, z), (х. у, z)
V
равна
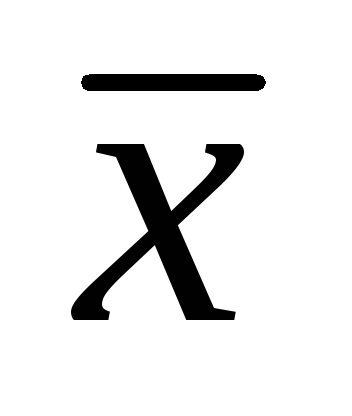 =My
/
M=(Gx(x,y)dxdy)
/ (G(x,y)dxdy)
=My
/
M=(Gx(x,y)dxdy)
/ (G(x,y)dxdy) -
Геометрический смысл тройного интеграла VdV есть объём области V
-
Если область V={(x,y,z):(x,y)G, (x,y) z (x,y)}, где функции и интегрируемы в G, то VdV равен двойному интегралу вида: Gdxdy(x,y)(x,y)dz=G((x,y)-(x,y))(x,y)dxdy
-
Момент инерции IOX относительно оси ОХ тела VR3 с плотностью (x,y,z), (x,y,z)V, равен IOX=V(y2+z2)(x,y,z)dxdydz
-
Ордината центра тяжести
 тела V
R3
с плотностью (x,y,z),
(x,y,z)V,
равна
тела V
R3
с плотностью (x,y,z),
(x,y,z)V,
равна
 =
MZX
/ M=
(Vy(x,y,z)dxdydz)/(V(x,y,z)dxdydz)
=
MZX
/ M=
(Vy(x,y,z)dxdydz)/(V(x,y,z)dxdydz) -
Момент инерции IZ относительно оси Oz тела V R3 с плотностью (x,y,z), (x,y,z) V, равен IZ=V(x2+y2)(x,y)dxdydz
-
Аппликата центра тяжести
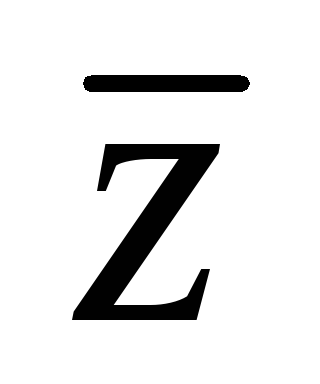 тела
V
R3
с плотностью (x,y,z),
(x,y,z)
R3
равна
тела
V
R3
с плотностью (x,y,z),
(x,y,z)
R3
равна
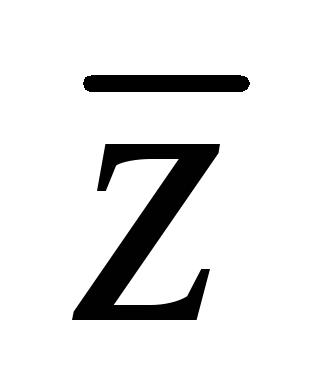 =MXY
/ M=
(Vz(x,y,z)dxdydz)/(V(x,y,z)dxdydz)
=MXY
/ M=
(Vz(x,y,z)dxdydz)/(V(x,y,z)dxdydz)
7
-
Масса тела V R3 с плотностью (x,y,z), (x,y,z) V равна M=V(x,y,z)dxdydz
-
По определению криволинейным интегралом второго рода от вектор-функции
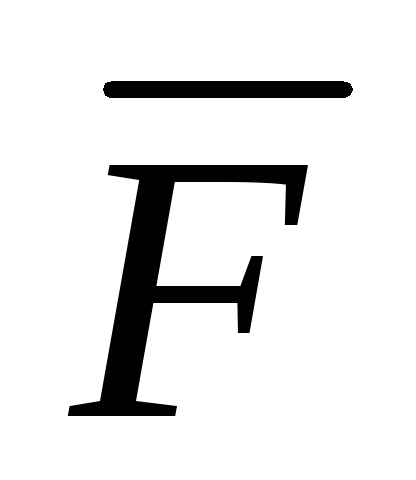 (х,у)
= Р(х,у)
(х,у)
= Р(х,у)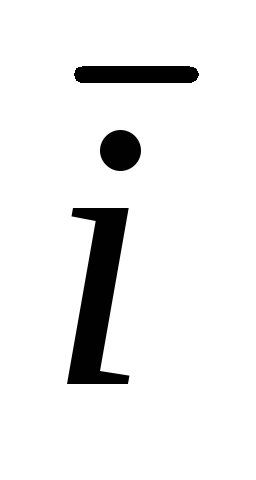 +Q(x,y)
+Q(x,y)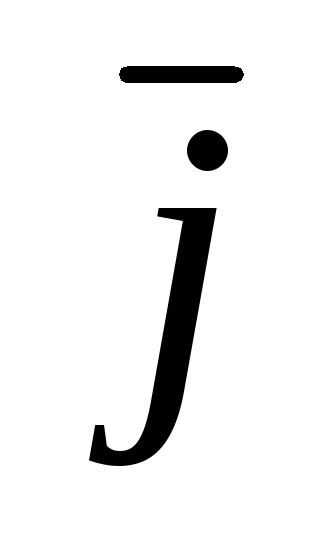 ,
непрерывной на ориентированной
кусочно-гладкой кривой АВ , называется
предел последовательности интегральных
сумм i=1n(
,
непрерывной на ориентированной
кусочно-гладкой кривой АВ , называется
предел последовательности интегральных
сумм i=1n(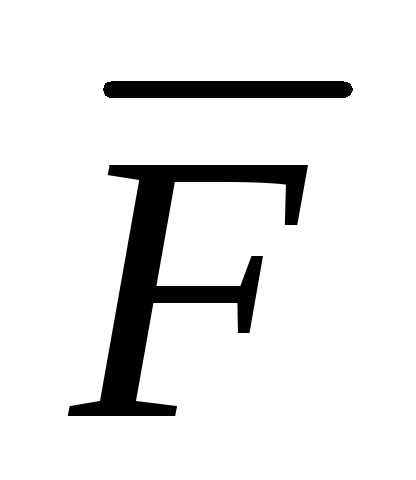 (Mi)
i)
при max
i0
который не зависит ни от способа деления
дуги (AB)
точками А
i
, ни от выбора точек М
i
, его обозначение (AB)(
(Mi)
i)
при max
i0
который не зависит ни от способа деления
дуги (AB)
точками А
i
, ни от выбора точек М
i
, его обозначение (AB)(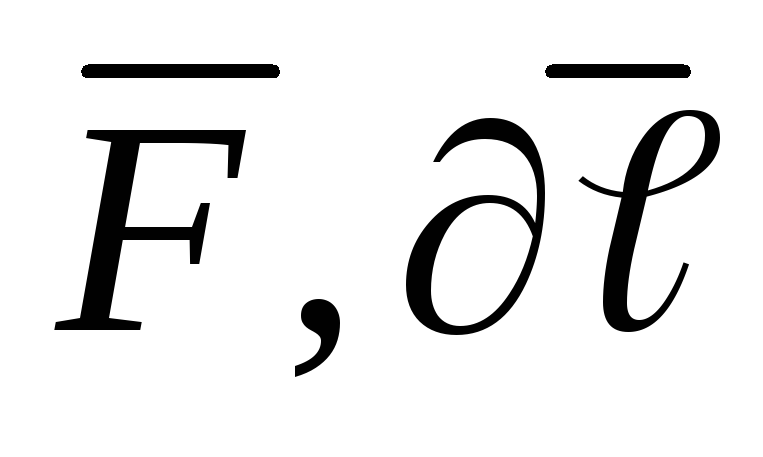 )=(AB)P(x,y)dx+Q(x,y)dy=
limmaxi0i=1n(
)=(AB)P(x,y)dx+Q(x,y)dy=
limmaxi0i=1n(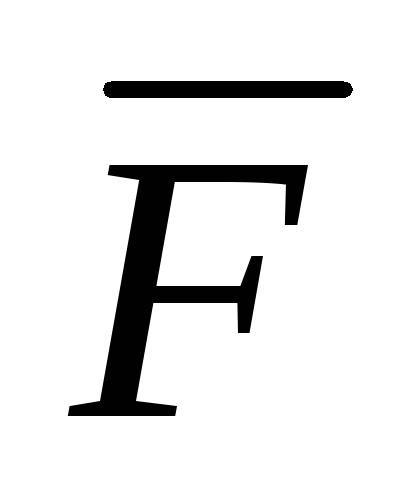 (Mi)
i)
(Mi)
i) -
Физический смысл криволинейного интеграла первого рода есть масса кривой АВ
-
Физический смысл криволинейного интеграла второго рода есть работа переменной силы по перемещению материальной точки из т.А в т.В вдоль кривой АВ
-
Если f(x,y) - непрерывная функция на кусочно-гладкой кривой АВ и I1=АВ(x,y)d , I2=ВА(x,y)d то I1=I2
-
Если P(x,y) и Q(x,y) - непрерывные функции на ориентированной кусочно-гладкой кривой АВ и I1=АВP(x,y)dx+Q(x,y)dy, I2=ВAP(x,y)dx+Q(x,y)dy, то I1= -I2
-
Циркуляцией вектора
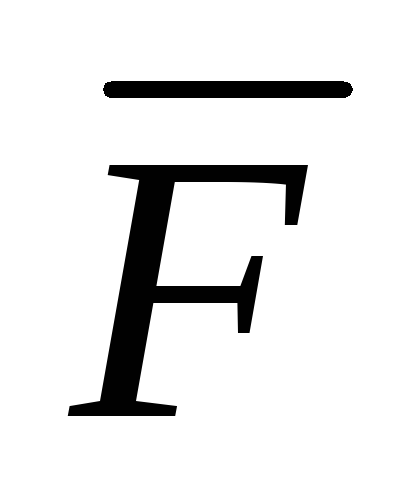 (x,y)=Р(х,у)
(x,y)=Р(х,у)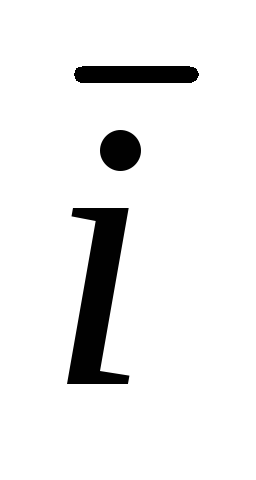 +Q(x,y)
+Q(x,y)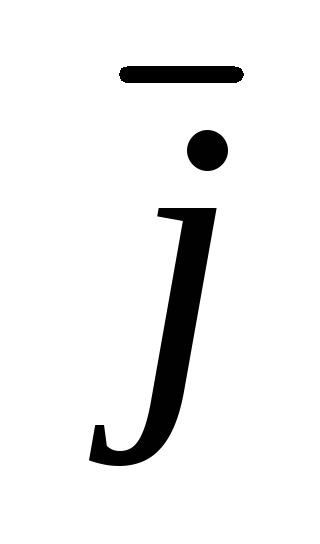 по
замкнутому кусочно-гладкому
ориентированному контуру L
называется криволинейный интеграл
второго рода по замкнутому контуру в
положительном направлении,
ее обозначение
по
замкнутому кусочно-гладкому
ориентированному контуру L
называется криволинейный интеграл
второго рода по замкнутому контуру в
положительном направлении,
ее обозначение
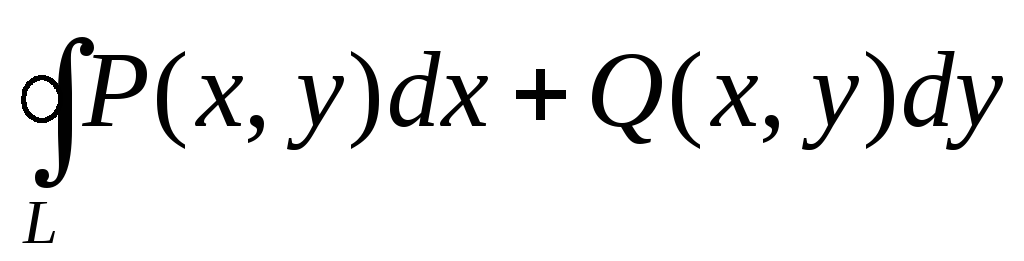
-
Интеграл вида AB(P(x,y)dx+Q(x,y)dy) называется криволинейным интегралом второго рода
-
Работа вектора силы
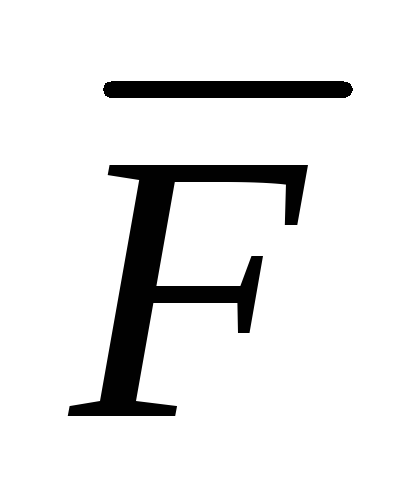 (x,y)=Р(х,у)
(x,y)=Р(х,у)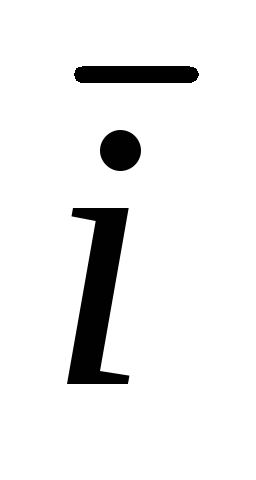 +Q(x,y)
+Q(x,y)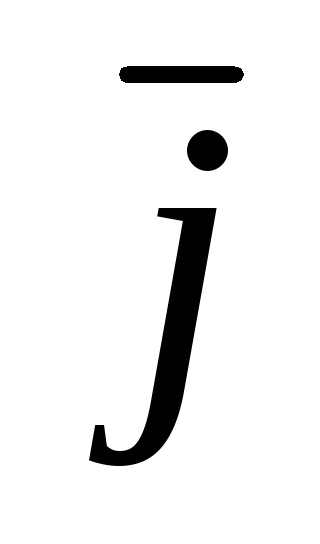 при перемещении вдоль кусочно-гладкой
кривой АВ
(
при перемещении вдоль кусочно-гладкой
кривой АВ
(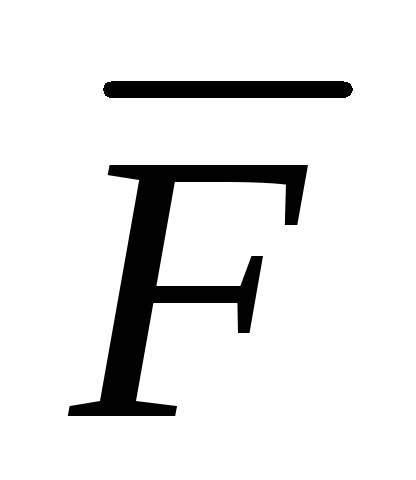 (x,y)
непрерывна
на АВ)
вычисляется по формуле:
A=AB(P(x,y)dx+Q(x,y)dy)
(x,y)
непрерывна
на АВ)
вычисляется по формуле:
A=AB(P(x,y)dx+Q(x,y)dy) -
Если Р(х,у) - непрерывная функция на кусочно-гладкой ориентированной кривой АВ и I1=АВP(x,y)dx, I2=ВAP(x,y)dx, то I1= I2
8
-
Если P(x,y) и Q(x,y) – непрерывные функции на кусочно-гладкой ориентированной кривой АВ состоящей из ситемы: x= (t), y= (t), где t1 t t2 ,то AB(P(x,y)dx+Q(x,y)dy) вычисляется по формуле: t1t2(P( (t), (t))(t)+Q( (t), (t))(t))dt
-
Если f(x,y) - непрерывная функция на кусочно-гладкой кривой АВ : у=у(х) (а х b), то ABf(x,y)dl вычисляется по формуле: ab(x,y(x))(1+(y(x))2)dx
-
Если Р(х,у) и- Q(x,y) - непрерывные функции на кусочно-гладкой ориентированной кривой АВ: y=f(x) (a x b), то ABP(x,y)dx+ Q(x,y)dy вычисляется по формуле: ab(P(x, f(x))+Q(x, f(x))(x))dx
-
Если f(x,y) - непрерывная функция на кусочно-гладкой кривой АВ : r = r() ( ), то ABf(x,y)dl вычисляется по формуле: (g()cos,r()sin )((r)2+(r)2)d
-
Если Р(х,у) и- Q(x,y) - непрерывные функции на кусочно-гладкой ориентированной кривой АВ: x= g(y) (c y d), то ABPdx+ Qdy вычисляется по формуле: ab(P(g(y),y)dy+Q(g(y),y))dy
-
Если f(x,y) - непрерывная функция на кусочно-гладкой кривой АВ состоящей из ситемы: x= (t), y= (t), где( t2 < t < t1 ) , то ABf(x,y)dl вычисляется по формуле: t1t2((t),(t))(((t))2+((t))2)dt
-
Если P(x,y,z),Q(x,y,z),R(x,y,z) -непрерывные функции на ориентированной кусочно-гладкой кривой АВ состоящей из ситемы: x= (t), y= (t), z=(t) где ( t2 < t < t1) , то ABP(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz вычисляется по формуле: t1t2(P( (t), (t), (t)) (t)+Q( (t), (t),(t))(t)+ R( (t), (t), (t))(t))dt
-
Если f(x,y,z) - непрерывная функция на кусочно-гладкой кривой АВ состоящей из ситемы: x= (t), y= (t), z=(t) где ( t1 < t < t2) , то ABf(x,y,z)dl вычисляется по формуле: t1t2((t),(t),(t))(((t))2+((t))2+((t))2)dt
-
Если Q(x,y,z) -непрерывная функция на ориентированной кусочно-гладкой кривой АВ состоящей из ситемы: x= (t), y= (t), z=(t) где ( t1 t t2) , то ABQ(x,y,z)dy вычисляется по формуле: t1t2Q((t),(t),(t))(t)dt
-
Если Р(х,у) и Q(x,y) непрерывные функции на кусочно-гладкой ориентированной кривой АВ, то ABP(x,y)dx+ Q(x,y)dy через криволинейный интеграл первого рода представляется в виде: AB(Pcos+Qsin)dl
9
-
Статический момент MOY относительно оси OY кусочно-гладкой кривой АВ с плотностью (х,у) вычисляется по формуле: MOY=ABx(x,y)dl
-
Момент инерции относительно начала координат кусочно-гладкой кривой АВ с плотностью (х,у) вычисляется по формуле: IO=AB(x2+y2)(x,y)dl
-
Момент инерции IOY относительно оси ОY кусочно-гладкой кривой АВ с плотностью (х,у), (х,у) АВ вычисляется по формуле: IY=ABx2(x,y)dl
-
Координаты
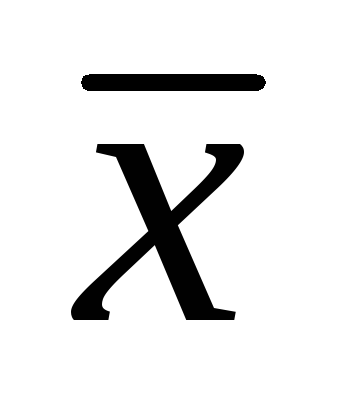 и
и
 центра
масс кусочно-гладкой кривой
АВ с
плотностью
(х,у),
(х,у)
АВ
вычисляются по формулам:
центра
масс кусочно-гладкой кривой
АВ с
плотностью
(х,у),
(х,у)
АВ
вычисляются по формулам:
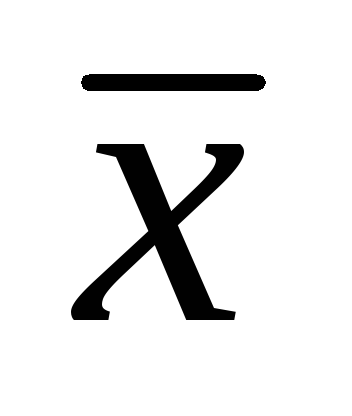 =My/M=(ABx(x,y)dl)
/ (AB(x,y)dl)
,
=My/M=(ABx(x,y)dl)
/ (AB(x,y)dl)
,
 =Mx/M=(ABy(x,y)dl)
/ (AB(x,y)dl)
=Mx/M=(ABy(x,y)dl)
/ (AB(x,y)dl) -
Момент инерции IOX относительно оси ОХ кусочно-гладкой кривой АВ с плотностью (х,у) вычисляется по формуле : IOX=ABy2(x,y)dl
-
Если f(x,y) и |f(x,y)| интегрируемы на кусочно-гладкой кривой АВ и I1=| AB(x,y)dl | , I2=AB|(x,y)|dl , то I1 I2
-
По свойству аддитивности, если (x,y) интегрируема на кусочно-гладкой кривой АВ, точка САВ, то AB(x,y)dl равен сумме интегралов вида: AC(x,y)dl+CB(x,y)dl
-
Масса кусочно-гладкой кривой AB по заданной плотности (х,у), (х,у)АВ вычисляется по формуле: m=AB(x,y)dl
-
Статический момент Mx относительно оси OX кусочно-гладкой кривой АВ с плотностью (х,у), (х,у)АВ вычисляется по формуле: Mx=ABy(x,y)dl
-
Если неотрицательная функция f(x,y) интегрируема на кусочно-гладкой кривой АВ, то для I=AB(x,y)dl справедливо, I 0
10
-
Для функций Р(х,у) и Q(x,y), непрерывных вместе с производными P/y и Q/x в замкнутой области G, ограниченной кусочно-гладкой ориентированной кривой L, формула Грина имеет вид: G(Q/x-P/y)dxdy
-
Если Р(х,у) и Q(x,y)—непрерывные функции в односвязной области G и
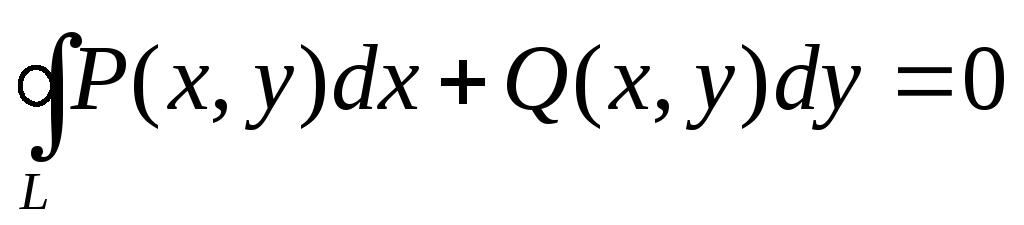 (L-произвольный ориентированный
замкнутый контур из G),
то для любых точек А и В из G интеграл
ABP(x,y)dx+Q(x,y)dy
не зависит от пути интегрирования , а
зависит только от расположения т.А и
т.В
(L-произвольный ориентированный
замкнутый контур из G),
то для любых точек А и В из G интеграл
ABP(x,y)dx+Q(x,y)dy
не зависит от пути интегрирования , а
зависит только от расположения т.А и
т.В -
С помощью криволинейного интеграла площадь области G, ограниченной кусочно-гладкой ориентированной кривой L, вычисляется по формуле:
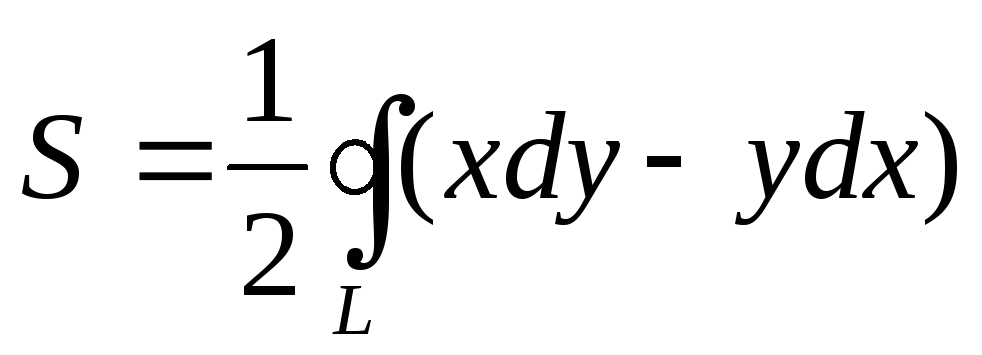
-
Если P(x,y) и Q(x,y) - непрерывные функции в односвязной области G и Pdx+Qdy=dU(x,y) (U(x,y) - функция, определенная в G), то для любых точек A и В из G ABPdx+Qdy не зависит от пути интегрирования , а зависит только от расположения т.А и т.В
-
Если P(x,y) непрерывна вместе с P/y в замкнутой области G, ограниченной кусочно—гладкой кривой L, то GP/ydxdy равен
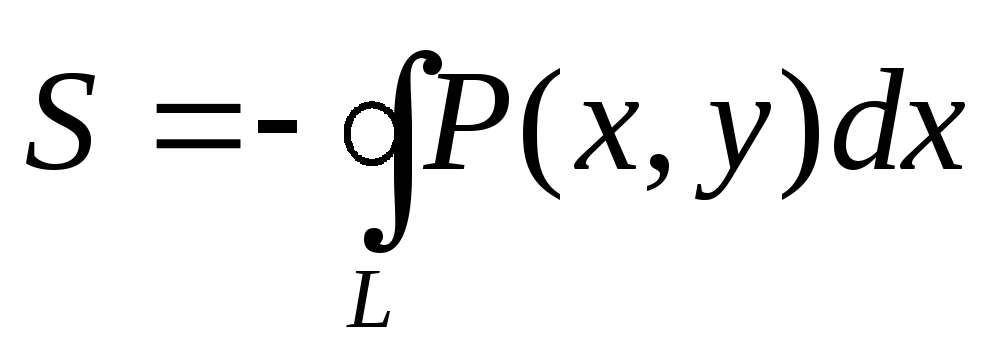
-
Если функции Р(х,у) и Q(х,y) непрерывны вместе с P/y и Q/x в односвязной области G , то для любых точек А и В из G ABPdx+Qdy не зависит от пути интегрирования , а зависит только от расположения т.А и т.В
-
Если функции P(x,y) и Q(х,y) -непрерывны в односвязной области G и для любых точек А и В ABPdx+Qdy не зависит от пути интегрирования, то существует функция U(x,y),определенная в G такая, что Pdx + Qdy есть полный дифференциал функции U(x,y)
-
Если функции P(x,y) и Q(x,y) - непрерывны в односвязной области G с кусочно-гладкой ориентированной границей Г и для любых точек А и В из G ABPdx+Qdy не зависит от пути интегрирования, а
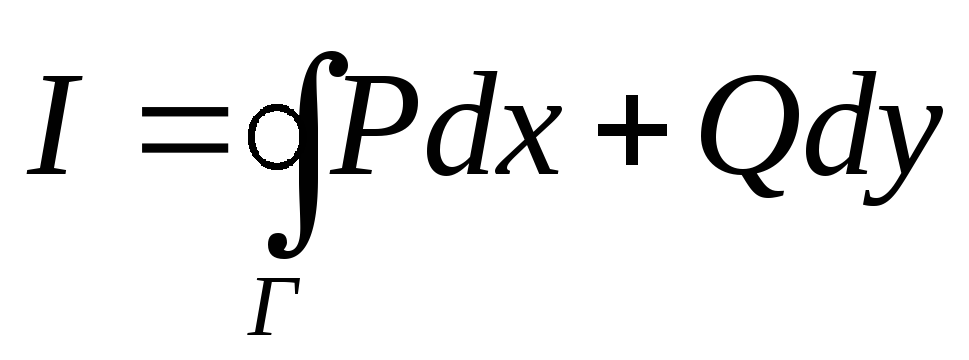 то I=0
то I=0 -
Если Q(x,y) непрерывна вместе с Q/x в замкнутой области G , ограниченной кусочно-гладкой кривой L, то GQ/xdxdy равен
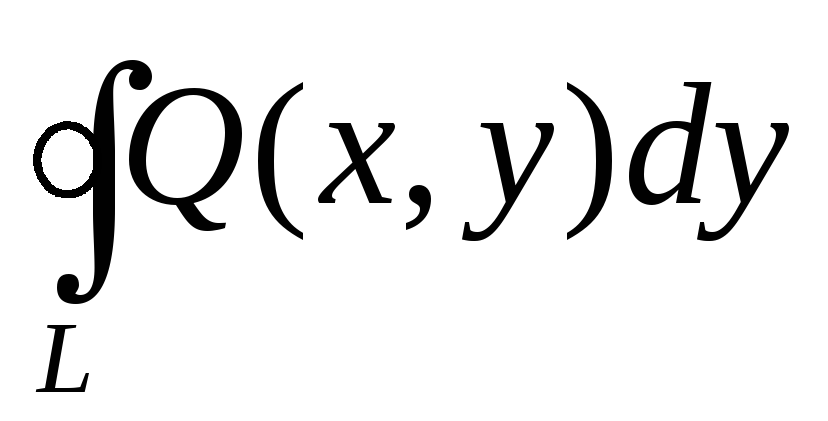
-
Если Р(х,у) и Q(x,y) непрерывны вместе с P/y и Q/x в односвязной области G и для любых точек А и В из G ABPdx+Qdy не зависит от пути интегрирования, то P/y = Q/x
