Заключение
В ходе выполнения работы были получены следующие результаты:
определено математическое ожидание выходного сигнала неустойчивого апериодического звена в заданный момент времени, которое при решении задачи разными методами составило:
при решении аналитически
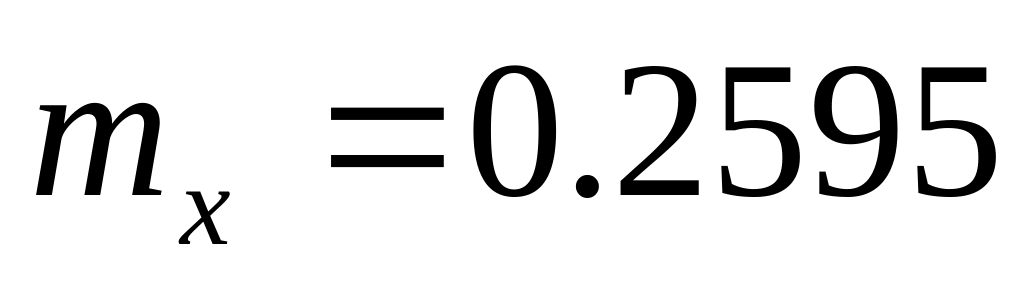;при решении прямым методом статистического моделирования
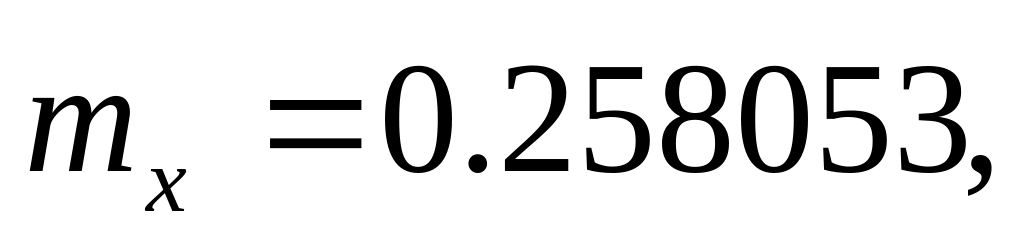(необходимо провести 20884 опытов);при решении комбинированным методом статистического моделирования
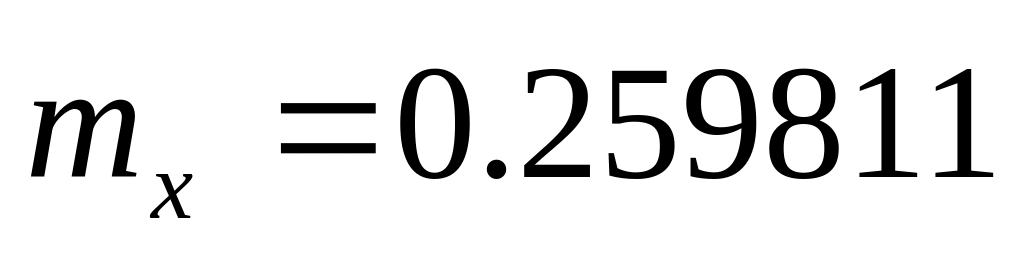(необходимо
провести 1967 опытов);
снижена трудоемкость статистического эксперимента в 10.8414 раза за счет выбора и проведения исследования упрощенной модели.
Список используемых источников
1. Емельянов В. Ю. Методы моделирования стохастических систем управления. Учебное пособие. СПб, 2004.
2. В. П. Дьяконов. MATLAB 7.*/R2006/R2007. Самоучитель.- М.: ДМК Пресс, 2008.
3.“Положение о курсовых проектах и курсовых работах на факультете информационных и управляющих систем (общие требования)”.
Приложение
Приложение А
clear all;
clc;
global A;
global G;
global a;
global k;
a = 0.5;
t = 1;
G = 1;
n = 0;
n_n=200;
disp('Номер итерации Mx Dx n_treb Общее кол-во опытов');
n_treb=n_n;
for i=n+1:n_treb
A = unifrnd(-0.5, 0.5);
k = unifrnd(0.2, 0.6);
x_k(i) = (A + k * G) * exp(a * t) - k * G;
end;
m=1;
s1=sum(x_k);
s2=sum(x_k .^ 2);
Mx = s1 / n_treb;
Dx = s2 / (n_treb - 1) - Mx ^ 2;
n=n_treb;
n_treb = round(9 / 0.0001 * Dx);
d = [m Mx Dx n_treb n];
fprintf(' %5.0f %8.6f %8.6f %5.0f %5.0f\n',d);
if n_treb>=n
n_treb=n_treb-n;
while 1;
m=m+1; % Количество итераций алгоритма
for i=n+1:n_treb
A = unifrnd(-0.5, 0.5);
k = unifrnd(0.2, 0.6);
x_k(i) = (A + k * G) * exp(a * t) - k * G;
end;
Mx=sum(x_k)/n_treb;
Dx=sum(x_k.^2)/(n_treb-1)-Mx^2;
n=n_treb;
n_treb=round(9*Dx/0.0001);
d=[m Mx Dx n_treb n];
fprintf(' %5.0f %8.6f %8.6f %5.0f %5.0f\n',d);
if (n>=n_treb)
break;
end;
end;
end;
Приложение Б
clear all;
clc;
global A;
global G;
global a;
global k;
a = 0.5;
t = 1;
G = 1;
n = 0;
m=0;
n_mas=[500 1000 2000];
n_n=30;
My1=3.5;
disp('Номер итерации Mx Dx n_treb Общее кол-во опытов');
n_treb=n_n;
while 1;
m=m+1;
for i=(n+1):n_treb
A = unifrnd(-0.5, 0.5);
k = unifrnd(0.2, 0.6);
x_k(i) = (A + k * G) * exp(a * t) - k * G;
Y(i)=A+7*a;
end;
n=n_treb;
Mx=sum(x_k)/n_treb;
Dx=sum(x_k.^2)/(n_treb-1)-Mx^2;
My=sum(Y)/n_treb;
Dy=sum(Y.^2)/(n_treb-1)-My^2;
teta=sum((x_k-Mx).*(Y-My1))/n_treb ;
Mx0=Mx-(teta/Dy)*(My-My1);
ro=teta/sqrt(Dx*Dy);
n_treb=round(9*Dx*(1-(ro.*ro))/0.0001);
v=1/(1-(ro*ro));
d=[m Mx0 Dx n_treb n v];
fprintf(' %5.0f %8.6f %8.6f %5.0f %5.0f %8.6f\n',d);
if (n>=n_treb)|(m==4)
break;
end;
if n_treb>n_mas(m)
n_treb=n_mas(m);
end;
end;
v=20848/n_treb