БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ "ВОЕНМЕХ"

им. Д. Ф. УСТИНОВА

Кафедра И3

КУРСОВАЯ работа

по учебной дисциплине: Стохастические системы управления

на тему: Сокращение трудоемкости статистического моделирования

студента: Шпилевского Сергея Сергеевича

группы И381

ПРЕПОДАВАТЕЛЬ

Королев С.Н. / ______________ /

Подпись

“___" _________________ 2012 г.

САНКТ-ПЕТЕРБУРГ

2012 г.

СОДЕРЖАНИЕ

Введение………………………………………………………………………………..3

1. Аналитическое решение………………………………………………………..4

2. Стандартная схема статистического моделирования………………………...6

3. Комбинированный метод получения оценки…………………………………8

ЗАКЛЮЧЕНИЕ…………………………………………………………………………..12

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ……………………………………13

Приложение А ……………………………………………………………….........14

Приложение Б ……………………………………………………………….........15

Введение

Требуется определить математическое ожидание выходного сигнала X неустойчивого апериодического звена в заданный момент времени T. Модель звена:

, ,

содержит случайные параметры с равномерным законом распределения в заданных интервалах.

Допустимая абсолютная погрешность .

Задачу решить тремя способами:

• используя стандартную схему статистического моделирования;

• используя рациональную схему статистического моделирования с применением комбинированного метода сокращения трудоемкости;

• аналитически.

Результаты аналитического решения использовать для проверки результатов статистического моделирования и для обоснования построения рациональной схемы моделирования.

При использовании рациональной схемы статистического моделирования обеспечить снижение требуемого количества опытов по сравнению со стандартной схемой не менее чем в 10 раз.

Исходные данные:

;

;

;

;

.

Основная часть

1 Аналитическое решение

Для того, чтобы аналитически найти математическое ожидание, было решено дифференциальное уравнение вида:

, , (1)

где A – случайный параметр, распределенный по равномерному закону на интервале [ ];

k – случайный параметр, распределенный по равномерному закону на интервале [ ].

Сначала нашли решение соответствующего однородного дифференциального уравнения:

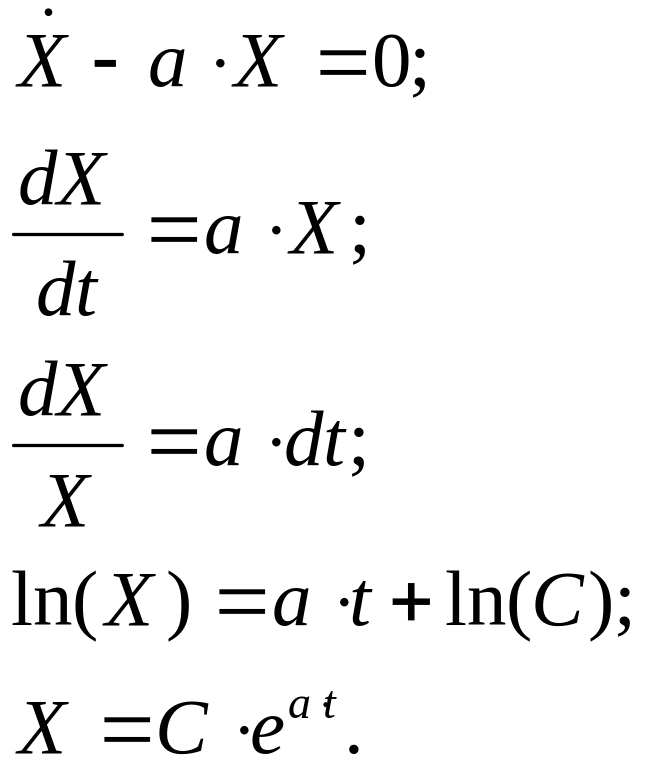
Подставив полученное решение однородного дифференциального уравнения (1):

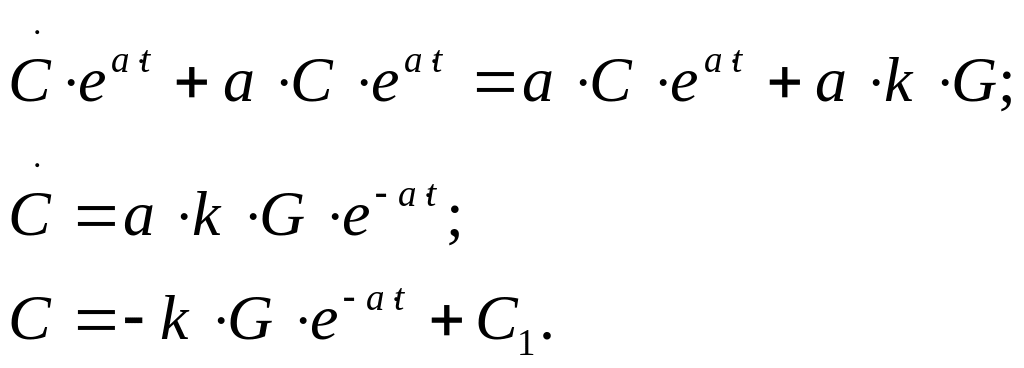
С₁ из условия X(0) = A:

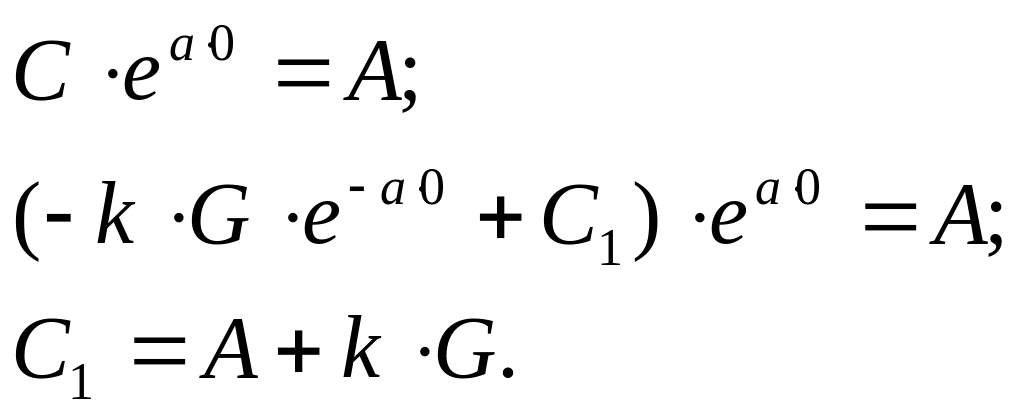
В результате получили:

Решение исходного дифференциального уравнения (1) имеет вид:

. (2)

Математическое ожидание выходного процесса определялось с учетом решения (2) [1]:

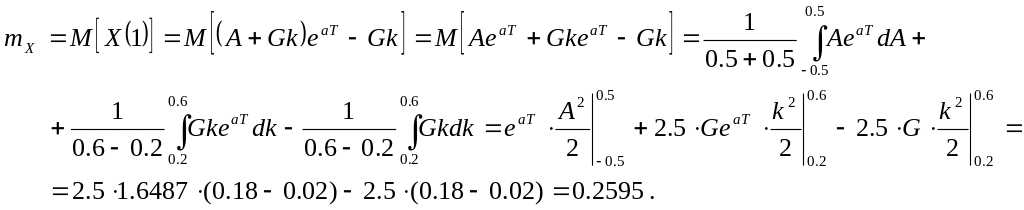(3)

Для нахождения требуемого количества опытов, проверки результатов статистического моделирования и обоснования построения рациональной схемы моделирования была посчитана дисперсия [1]:

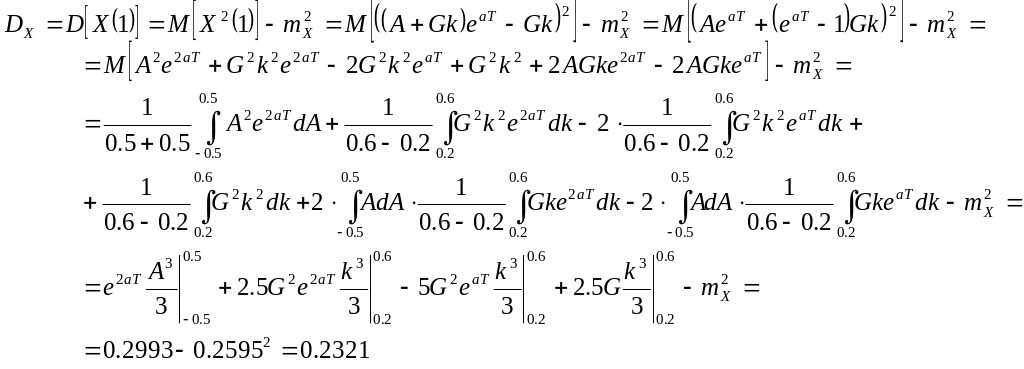(4)

Используя полученное аналитически значение дисперсии оценили требуемое количество опытов [1]:

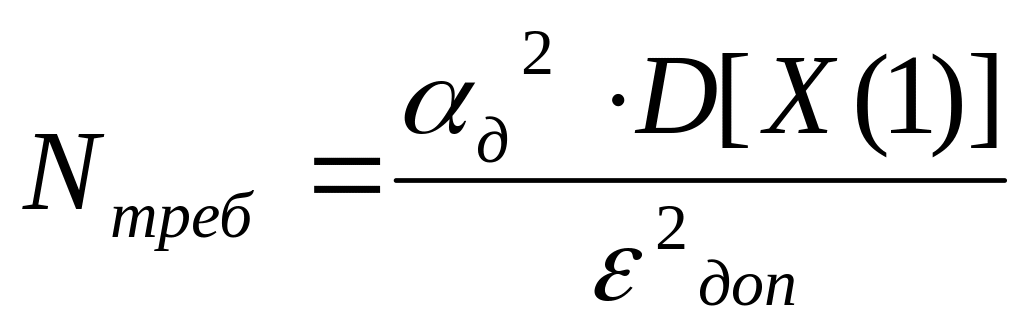, (5)

где параметр принят равным 3 (при доверительной вероятности Р_д=0,997).

Подставив в формулу (5) значение, полученное по формуле (4), получили требуемое количество опытов 20880.

2 Стандартная схема статистического моделирования

Если трудоемкость эксперимента имеет существенное значение, применяются итерационные алгоритмы получения оценок [1]. Идея итерационных алгоритмов состоит в том, что определение точности и требуемого количества опытов проводится в ходе эксперимента на основе получаемых оценок искомых параметров.

Блок-схема типового итерационного алгоритма приведена на рисунке 1.

Рисунок 1 - Блок-схема итерационного алгоритма

Для задачи оценки математического ожидания случайной величины x предусматривается:

1. Проведение начальной серии опытов объемом n и накопление сумм

,

где - реализация случайной величины x в отдельных опытах.

2. Вычисление оценок математического ожидания 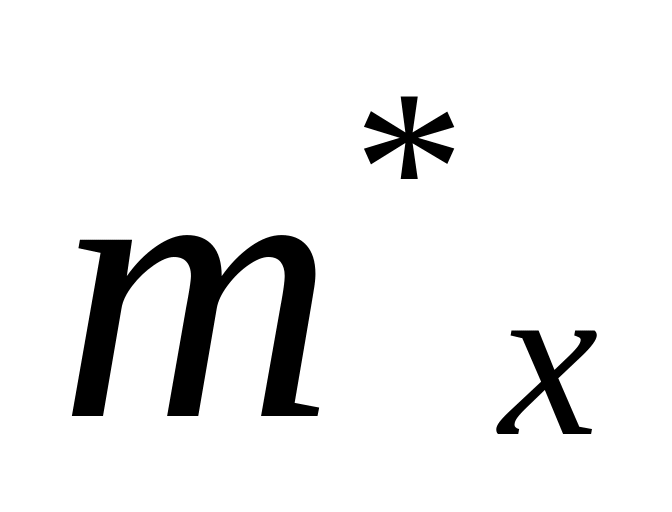и дисперсии :

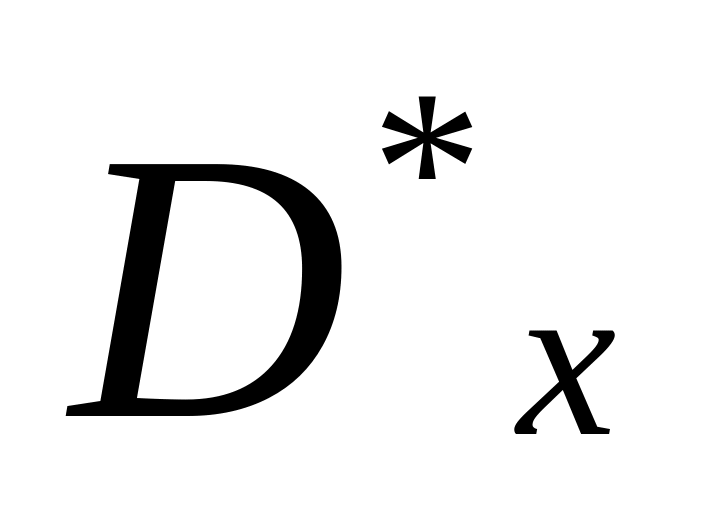, (6)

. (7)

3. Получение оценки требуемого количества опытов:

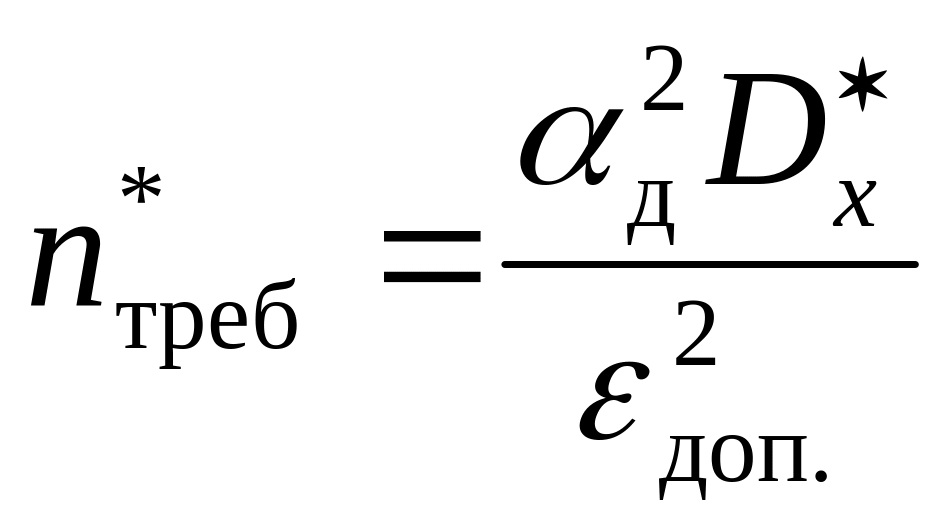. (8)

4. Проведение дополнительной серии опытов объемом 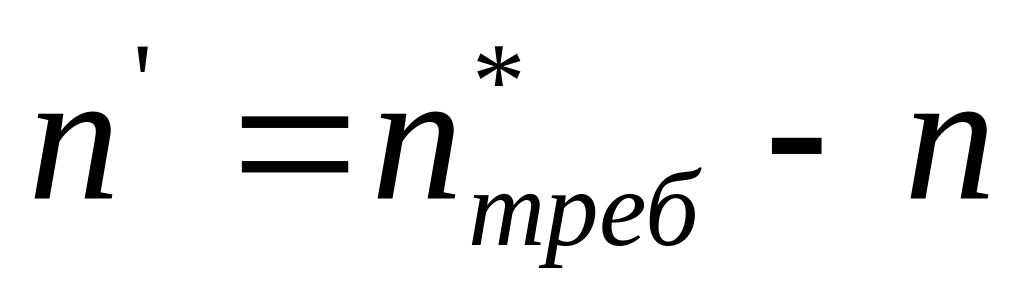и накопление сумм:

, .

5. Уточнение оценок математического ожидания m^*_x и дисперсии D^*_x:

, (9)

. (10)

Провели начальную серию опытов n = 200. Вычислили оценки математического ожидания и дисперсии по (6) и (7): Получили оценку требуемого количества опытов по (8):

Проверили выполнение условия . Так как , то провели дополнительную серию опытов Уточнили оценки математического ожидания и дисперсии по (9) и (10): Тогда оценка требуемого количества опытов получилась:

Проверили выполнение условия . Так как 21165>20848, условие выполнилось, следовательно, алгоритм завершил работу.

Окончательные результаты:

При решении поставленной задачи численное интегрирование исходного уравнения проводилось на ЭВМ в среде Matlab7 [2]. При этом значения случайных параметров уравнения получались с помощью встроенной функции unifrnd. Текст программы, проводящей данные вычисления, представлен в приложении А.