5.3. Оцінка ймовірності втрат комутаційних схем за методом імовірнісних графів

Как было указано в предыдущем разделе существенное уменьшение числа точек коммутации возможно, если коммутационная схема будет работать с блокировками. Однако вероятность блокировки является одним из параметров качества обслуживания, поэтому ее значение не должно превышать некоторой заданной величины.

Таким образом, при использовании блокируемых коммутационных схем необходимо знать, как оценить вероятность блокировки. Один из наиболее универсальных и концептуально простых методов оценки вероятности блокировки коммутационных схем основан на использовании вероятностных графов. Хотя этот метод требует некоторых упрощающих допущений, он дает результат с приемлемой погрешностью, особенно когда сравнение альтернативных структур важнее, чем получение точного результата. Достоинства этого метода состоят в простоте формулировки, а также в том, что формулы непосредственно связаны с исследуемой структурой коммутационной схемы. Таким образом, данный метод помогает понять, каким образом необходимо модифицировать коммутационную схему для получения заданных параметров.

Метод імовірнісних графів ґрунтується на поданні комутаційної схеми у вигляді графа, вид якого залежить не тільки від структури комутаційної схеми, але й від режиму пошуку в якому використовується ця схема. Імовірнісний граф може належати до класу паралельно-послідовних графів або до класу непаралельно-послідовних (місткових) графів.

Метод імовірнісних графів дозволяє записати функцію для ймовірності втрат при встановленні з'єднань у графі, який відповідає комутаційній схемі, що аналізується, між його вхідними й вихідними полюсами, аргументами якої є ймовірності зайнятості окремих дуг графа. Для визначення ймовірності зайнятості дуг використовують значення середньої інтенсивності навантаження, що обслуговується кожною з них.

Записана в такий спосіб функція дозволяє визначити ймовірності втрат або оптимізувати структуру за кількістю точок комутації або іншими показниками.

Далі будемо проводити аналіз типової триланкової комутаційної схеми, яка зображена на рисунку 5.19.

Рисунок 5.19 – Триланкова комутаційна схема

Будемо вважати, що комутаційна схема однозв'язна, а структурні параметри схеми задовольняють таким співвідношенням: ; ; ; .

На рисунку 5.20, а наведений імовірнісний граф триланкової комутаційної схеми, використовуваної в режимі лінійного шукання, а на рисунку 5.20, б його спрощене подання.

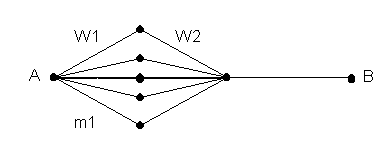
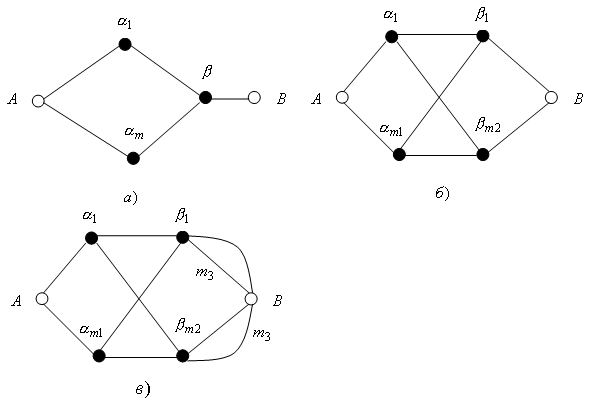
Рисунок 5.20 – Імовірнісний граф триланкової комутаційної схеми для випадку лінійного шукання

Дуги , що з'єднують вхідний полюс А з вершинами , зображують проміжні лінії між ланками 1 і 2, дуги , що з'єднують вершини з вершиною , зображують проміжні лінії між ланками 2 і 3, а дуга , що з'єднує вершину з вихідним полюсом , зображує вихід комутаційної схеми, до якого має бути підключений заданий вхід при використанні схеми в режимі лінійного шукання.

На рисунку 5.21, а наведений імовірнісний граф триланкової комутаційної схеми, використовуваної в режимі групового шукання, а на рисунку 5.21, б його спрощене подання. Граф зображений для випадку, коли з кожного блоку комутації третьої ланки в напрямку групового пошуку береться по одному виходу.

На цьому рисунку, як і на попередньому, дуги зображують проміжні лінії між ланками 1 і 2, дуги – проміжні лінії між ланками 2 і 3, а дуги – виходи потрібного напрямку, до одного з яких має бути підключений заданий вхід.

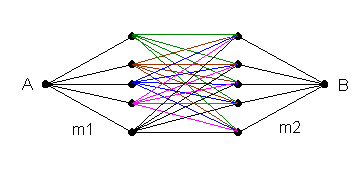
Рисунок 5.21 – Імовірнісний граф триланкової комутаційної схеми для випадку групового шукання

На рисунку 5.22, а наведений імовірнісний граф триланкової комутаційної схеми, використовуваної в режимі вільного шукання, у якому певний вхід має бути підключений до одного з вільних виходів всієї схеми, а на рисунку 5.22, б його спрощене подання. Цей граф відрізняється від попереднього тільки тим, що між кожною вершиною й полюсом В є не одна, а дуг, що зображують виходів з кожного блоку комутації третьої ланки.

Якщо в режимі групового пошуку для розглянутого напрямку в кожному з комутаторів третьої ланки використовується виходів, то структура графа буде тією ж самою, як показано на рисунку 5.22, тільки між вершинами і полюсом В буде дуг замість .

Рисунок 5.22 – Імовірнісний граф триланкової комутаційної схеми для випадку вільного шукання

Таким чином, у режимі лінійного пошуку триланкова комутаційна схема має граф паралельно-послідовного типу, а в режимах групового і вільного пошуків – граф непаралельно-послідовного типу. Збільшення кількості ланок комутаційної схеми призводить до зростання кількості ланок графу, однак його принцип побудови залишається незмінним. Тому, для прикладу, розглянемо побудову імовірнісного графу для чотириланкової комутаційної схеми, побудованої ітераційним способом на основі дволанкових блоків комутації, яка була зображена на рисунку 5.17. Імовірнісні графи такої чотириланкової комутаційної схеми показано на рисунку 5.23.

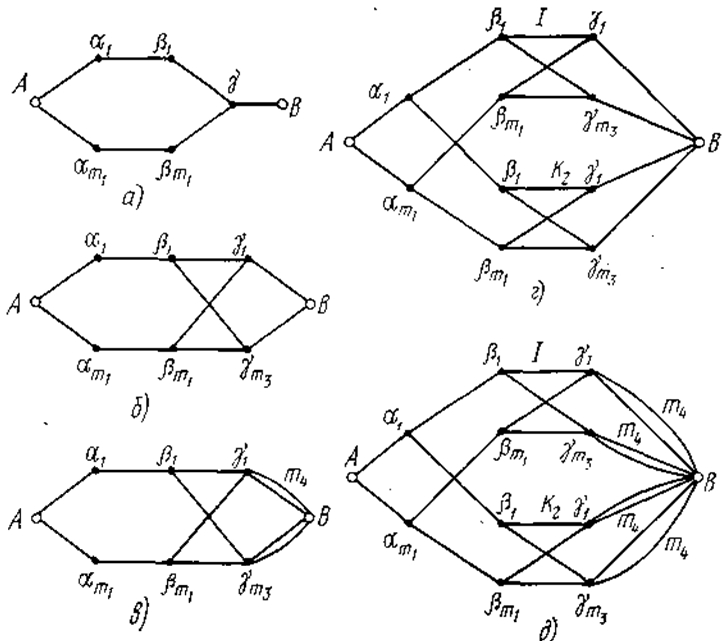
Рисунок 5.23 – Імовірнісні графи чотириланкової

комутаційної схеми для режимів: лінійного шукання (а), групового шукання (б, в, г) та вільного шукання (д)

На рисунке 5.23, а приведен граф для режима линейного искания. В режиме группового искания рассматриваемая четырехзвенная схема будет иметь один из графов, приведенных на рисунках 5.23, б, в, г. Первый из этих графов соответствует случаю, когда к выходам одной группы относятся по одному выходу из каждого коммутатора только одного двухзвеньевого блока. Второй граф соответствует случаю, когда все выходы этого двухзвеньевого блока образуют искомую группу выходов. Третий граф справедлив для случая, когда группа выходов образуется путем использования по одному из выходов от каждого коммутатора всей схемы. В режиме свободного искания рассматриваемая схема будет соответствовать графу на рисунке 5.23, д.

Запис функції втрат виду , де – імовірність втрат, а – ймовірність зайнятості кожної дуги -ї ланки, зводиться для графів паралельно-послідовного типу, вважаючи незалежність подій, що відбуваються в різних ланках графа, до множення й підсумовування ймовірностей .

При цьому у випадку паралельного включення декількох дуг, що утворюють деяку загальну гілку, для одержання ймовірності зайнятості всієї гілки обчислюють добуток ймовірностей зайнятості окремих дуг (рисунок 5.24).

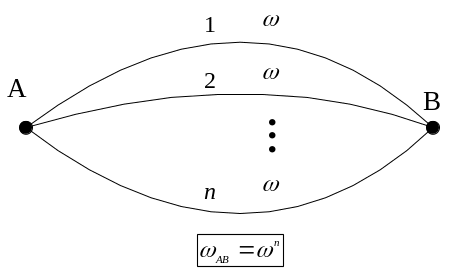
Рисунок 5.24 – Визначення ймовірності заняття усіх шляхів між полюсами А та В при паралельному включенні дуг графа

Якщо гілка утворюється послідовним включенням (ланцюжком) дуг, то ймовірність зайнятості всієї гілки визначається як додаткова ймовірність до ймовірності вільності всієї гілки, а ймовірність вільності всієї гілки , в свою чергу, визначається як добуток ймовірностей вільності окремих послідовно включених дуг (рисунок 5.25).

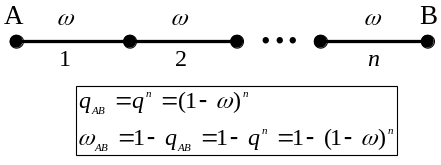
Рисунок 5.25 – Визначення ймовірності заняття шляху між полюсами А та В при послідовному включенні дуг графа

Знайдемо ймовірність втрат для триланкової комутаційної схеми для випадку лінійного шукання (рисунок 5.20)

Позначимо ймовірність зайнятості дуг для паралельно-послідовного графа, наведеного на рисунку 5.18 відповідно (для дуг ), для дуг й (для дуги ), а ймовірності вільності цих же дуг через , , . Тоді ймовірність того, що один зі шляхів між полюсом А і вершиною , що складається із двох дуг, буде вільний, складе , а ймовірність зайнятості цього шляху . Імовірність зайнятості всіх шляхів між полюсом А і вершиною дорівнюватиме

. (5.11)

Для того щоб підрахувати ймовірність втрат комутаційної схеми , яка дорівнює ймовірності зайнятості всіх можливих шляхів між полюсами А і В - , визначимо ймовірність вільності хоча б одного шляху між полюсами А і В - як добуток ймовірностей вільності гілки й дуги :

.

У свою чергу ймовірність втрат дорівнюватиме

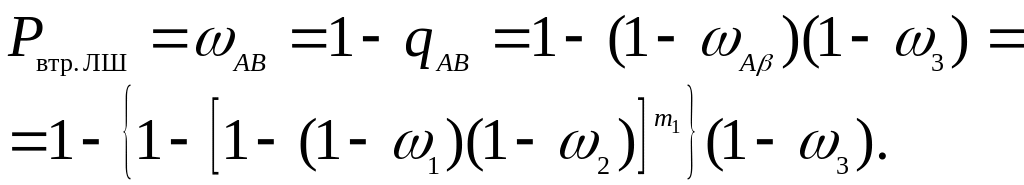(5.12)

Використовуючи аналогічні міркування для режимів групового й вільного шукання можна одержати, відповідно, такі співвідношення:

; (5.13)

; (5.14)

Отметим, большинство рассмотренных вероятностных графов принадлежат к классу непараллельно-последовательных графов и в их структуре существенную роль играет простейший непараллельно-последовательный (мостиковый) граф, показанный на рисунке 5.21. Формула для вычисления вероятности потерь для такого мостикого графа имеет вид

, (5.15)

где , , , - вероятности занятости дуг графа на рисунке 5.21.

Поэтому, во многих случаях вычисление вероятности потерь для сложных непараллельно-последовательных графов сводится к приемам, применимым для параллельно-последовательных графов в сочетании с формулой (5.15).

У формулах (5.12) – (5.14) значення , , визначаються як

; (5.16)

; (5.17)

, (5.18)

де - ймовірність зайняття однієї вихідної лінії комутаційної схеми.

Імовірності заняття проміжних ліній між ланками комутаційної схеми визначаються виразами (5.16) – (5.18). Розглянемо сутність цих виразів на прикладі виразу (5.16), який визначає ймовірність заняття однієї проміжної лінії між першою та другою ланками триланкової комутаційної схеми.

Перепишемо (5.15) у виді:

, (5.18)

де - коефіцієнт розширення для першої ланки.

Выражение (5.18) показывает, что если занято некоторое число входов, то занято и такое же число выходов первого звена, однако число промежуточных линий в раз отличается от числа входов, поэтому относительное число занятых промежуточных линий измениться в раз.

Если , то и это означает, что первое звено коммутационной схемы обеспечивает пространственное расширение. Если , то . В этом случае первое звено коммутационной схемы обеспечивает пространственное сжатие (концентрацию).

Тепер ще раз розглянемо вираз (5.12). Останній множник в ньому - визначає ймовірність заняття одного виходу триланкової комутаційної схеми. Якщо знаходити ймовірність внутрішнього блокування триланкової комутаційної схеми в припущенні, що вхід та вихід, які необхідно з’єднати, вільні, то можна користуватися таким виразом:

. (5.19)

Для триланкової комутаційної схеми, зображеної на рисунку 5.12 (випадок ), справедливі такі параметри:

; ;

;

.

Ймовірності зайняття проміжних ліній визначимо, як

; .

Для цього випадку (5.18) буде мати вид:

. (5.20)

В таблице 5.2 приведено число точек коммутации, рассчитанных по формуле (5.20), для коммутационных схем той же емкости, которые представлены в таблице 5.1. Число блоков коммутации центрального звена в каждом случае было выбрано так, чтобы обеспечить вероятность блокировки . Вероятность занятия выходных линий в каждом примере была принята равной 0,1 ( ).

Из анализа таблицы 5.2 следует, что наибольшая экономия в числе точек коммутации для коммутационных схем большой емкости достигается за счет введения большего коэффициента концентрации ( ) в первом звене. При большой вероятности занятия выходных линий ( ), наоборот, будет наблюдаться расширение ( ) в первом звене (таблица 5.3).

Таблиця 5.2 – Параметры трехзвенных коммутационных схем при ,

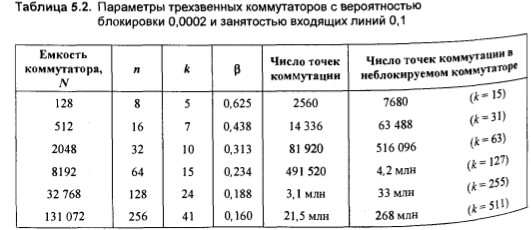
Таблиця 5.3 – Параметры трехзвенных коммутационных схем при ,

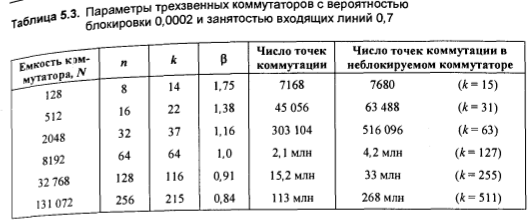
Результаты, приведенные в таблицах 5.2 и 5.3, показывают, что коммутационные схемы большой емкости все еще нуждаются в большом числе точек коммутации, даже если допускается блокировка. Поэтому, коммутационные схемы большой емкости могут иметь более трех звеньев для еще большего сокращения числа точек коммутации.

Переход к пятизвенной коммутационной схеме, изображенной на рисунке 5.14, для случая, когда три средние звена являются неблокируемые ( ) позволяет сэкономить 8704 точки коммутации на каждом коммутаторе центрального звена трехзвенного коммутатора емкостью 32768 линий, представленного ранее в таблице 5.3.

Следовательно, при построении пятизвенной коммутационной схемы емкостью 32 768 линий, параметры которой даны в таблице 5.3, можно сэкономить более 1 млн. точек коммутации. На практике возможен вариант, когда средние звенья пятизвенной схемы работают с блокировками, что позволяет еще больше уменьшить число точек коммутации.

Вероятностный граф для пятизвенной коммутационной схемы показан на рисунке 5.26. На основании данного графа вероятность блокировки определяется как

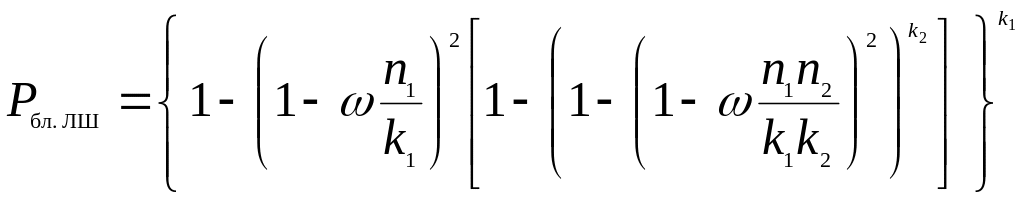. (5.21)

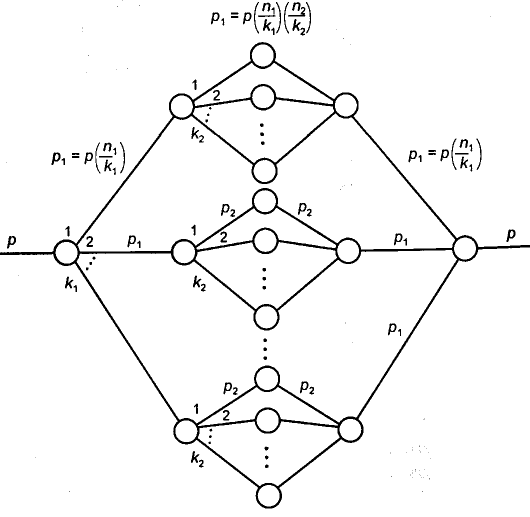
Рисунок 5.26 – Вероятностный граф для пятизвенной коммутационной схемы

Теперь рассмотрим обобщенный алгоритм нахождения вероятности потерь многозвенной коммутационной схемы с произвольным количеством звеньев, показанной на рисунке 5.27. На этом рисунке приняты следующие обозначения:

- число звеньев коммутации;

- число блоков коммутации в g-ом звене;

- число входов блока коммутации g-го звена;

- число выходов блока коммутации g-го звена;

- емкость блока коммутации -го звена;

- связностью между -ым и -м звеньями;

- число пучков ПЛ.

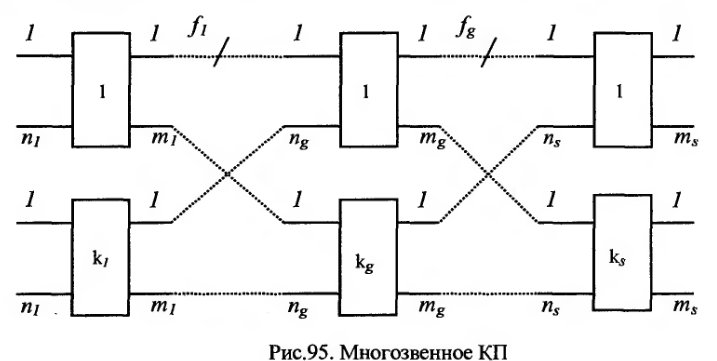
Рисунок 5.27 – Многозвенная коммутационная схема с произвольным количеством звеньев

В режиме группового искания число линий каждого -го направления ( ) равномерно распределяется между коммутаторами -го звена, при этом число выходов в направлении j из одного блока коммутации последнего звена

.

Исходными данными для расчета являются интенсивности нагрузок, , обслуженные каждым -ым направлением.

В соответствии с режимом искания составляется вероятностный граф, в котором каждая из ветвей, состоящая из ПЛ, занята с вероятностью

и свободна с вероятностью , причем

; ; ; ,

где - интенсивность нагрузки, обслуженной одной ПЛ;

- интенсивность нагрузки, обслуженная всей коммутационной схемой;

- число линий -го направления ( );

- интенсивность нагрузки, обслуженная одной выходной линией -го блока коммутации в -м направлении ( );

- интенсивность нагрузки, обслуженная -ым направлением;

- число пучков ПЛ между -ым и -м звеньями;

- число выходов в j-ом направлении из одного блока коммутации последнего звена.

Потери вычисляются как вероятность отсутствия свободных соединительных путей к требуемому выходу (или выходам). Расчет производится рекуррентно от -го звена к первому звену.

При вычислении потерь для многозвенной схемы в режиме группового искания выполняют следующие действия.

1. Вычисляют вероятность занятия всех выходов одного коммутатора -го звена для -го направления:

.

2. Вычисляют вероятность потерь в направлении от входа коммутатора -го звена до выхода коммутационной схемы:

.

3. Вычисляют вероятность потерь в направлении от входа -го звена до выхода коммутационной схемы:

.

… … …

4. Вычисляют вероятность потерь в направлении от входа 1-го звена до выхода коммутационной схемы, она же - искомая вероятность потерь многозвенной коммутационной схемы для -го направления:

. (5.22)

Интенсивность нагрузки, поступающей в j-oe направление, находится из равенства:

, (5.23)

а общая интенсивность нагрузки, поступающая на коммутационную схему, находится как

.

Примечание 1. В режиме свободного искания принимается , и, далее следуют процедуре вычисления потерь в режиме группового искания.

В режиме линейного искания принимается , и, далее следуют процедуре вычисления потерь в режиме группового искания.

Примечание 2. Если заданы не обслуженные интенсивности нагрузок для каждого направления, а поступающие интенсивности нагрузок , то вероятность потерь в -ом направлении вычисляется итерационно:

а) на первой итерации принимают интенсивность обслуженной нагрузки ;

б) по формуле (5.22) находят вероятность потерь ;

в) по формуле (5.23) вычисляют значение поступающей нагрузки ;

г) оценивают погрешность вычисления:

,

где - требуемая точность вычислений.

При выполнении неравенства процесс вычисления вероятности потерь заканчивают.

При невыполнении неравенства процесс вычисления вероятности потерь продолжают с пункта б), но для нового значения интенсивности обслуженной нагрузки:

.

И в заключение, отметим основной недостаток метода вероятностных графов – его невысокую точность. Действительно, можно сразу заметить, что вероятность потерь не равна нулю даже при выполнении условия неблокируемости Клоза, что говорит о наличии погрешности в результатах, получаемых с помощью метода вероятностных графов. Однако данный метод обеспечивает приемлемую погрешность для значений , которые выполняются в большинстве практических случаев.

Пример. Вывести выражение расчета вероятности потерь в режиме линейного искания для трезвенной коммутационной схемы с такими параметрами: , , , , , , , , , . Считать, что интенсивность обслуженной нагрузки всей коммутационной схемой равна .

Решение. Определяем интенсивность обслуженной нагрузки ПЛ между 1-м и 2-м звеньями:

,

а также между 2-м и 3-м звеньями:

.

Теперь находим вероятность потерь:

;

.

Пример. Рассчитать вероятность потерь в режиме группового искания двузвенной коммутационной схемы с такими параметрами: , , , , . Интенсивность нагрузки, обслуженная 1-м направлением, составляет , а вторым - .

Решение. Определяем интенсивность обслуженной нагрузки одной линией на выходе 2-го звена в 1-ом направлении:

.

Затем определяем интенсивность обслуженной нагрузки одной линией на выходе 2-го звена в 2-ом направлении:

.

Определяем интенсивность обслуженной нагрузки одной ПЛ линией между 1-м и 2-м звеньями:

.

Вычисляем вероятность потерь для 1-го направления:

;

.

Вычисляем вероятность потерь для 2-го направления:

;

.

Интенсивность нагрузки, поступающая в 1-e и 2-е направления:

;

.

Суммарная интенсивность нагрузки, поступающая на коммутационную схему:

.