5 Принципи побудови схем просторової комутації

5.1 Одноланкові комутаційні схеми

Анализ характеристик коммутационных полей осуществляется путем представления коммутационного поля (или его части) в виде коммутационной схемы, которая отражает основное свойство коммутационного поля – осуществление коммутации, т.е. соединение заданного входа коммутационного поля с заданным выходом. Коммутационные элементы (коммутационные приборы, устройства) которые входят в состав коммутационного поля, с целью скрытия особенностей их реализации называются точками коммутации. Таким образом, под точкой коммутации следует понимать некоторый элемент с двумя возможными состояниями: «замкнуто» или «разомкнуто».

Такое условное представление коммутационного поля позволяет проводить его анализ без учета особенностей аппаратной реализации и подходит для анализа как цифровых, так и аналоговых коммутационных полей. Отметим, что при цифровой коммутации в качестве коммутационного элемента используется логический элемент (рисунок 5.1).

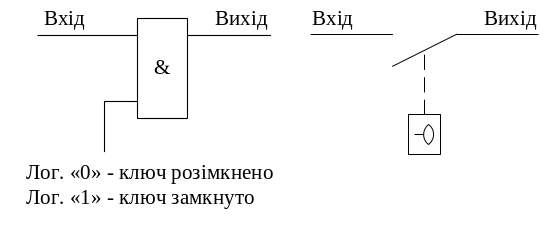
а) б)

Рисунок 5.1 – Комутаційний елемент цифрового комутаційного поля (а), його еквівалентна схема (б)

Схематично просторову комутаційну схему можна представити у вигляді прямокутних грат, складених з точок комутації так, як показано на рисунку 5.2. Ця комутаційна схема може бути використана для з’єднання будь-якого з N входів з будь-яким з М виходів.

Рисунок 5.2 – Приклад повнодоступної комутаційної схеми

Комутаційна схема може бути повнодоступною чи неповнодоступною. Якщо будь-який вхід комутаційної схеми може бути з’єднаний з будь-яким виходом, то таку комутаційну схему називають повнодоступною. І навпаки, якщо вхід комутаційної схеми може буди з’єднаний тільки з обмеженою кількістю виходів (а не з усіма), то таку комутаційну схему називають неповнодоступною.

В комутаційній схемі, що зображена на рисунку 5.1, на кожному перехресті вхідних та вихідних ліній знаходиться точка комутації. Це дозволяє встановлювати з’єднання будь-якого входу комутаційної схеми з будь-яким виходом за допомогою тільки однієї точки комутації.

Для деяких випадків вимога забезпечення можливості встановлення з’єднання будь-якого входу з будь-яким виходом не є обов’язковою. Так, у разі, коли кількість виходів в групі достатньо велика, можна забезпечити кожному входу доступ не до всіх, а лише до обмеженої кількості виходів. У таких випадках використовують неповнодоступні комутаційні схеми.

Приклад неповнодоступної комутаційної схеми приведений на рисунку 5.3. З аналізу рисунку випливає, що перший та другий входи можуть бути з’єднані тільки з першим та четвертим виходом, третій вхід – з першим та другим виходами і т.д.

Перехід до неповнодоступних комутаційних схем дозволяє одержати значну економію точок комутації. Неповнодоступні комутаційні схеми знайшли широке використання практично в усіх аналогових системах комутації, де вартість точки комутації достатньо висока і розміри окремих комутаційних модулів обмежені. Також вони використовуються на окремих ланках комутації багатоланкових цифрових комутаційних полів, де існує більше одного шляху до будь-якого заданого виходу. Тому більш детальний аналіз неповнодоступних схем буде проведено в окремому розділі.

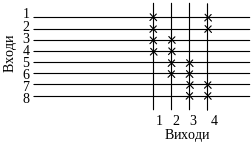
Рисунок 5.3 – Приклад неповнодоступної комутаційної схеми

Комутаційні поля як цифрових, так і аналогових систем комутації повинні мати дуже багато входів та виходів, тому безпосередня реалізація комутаційної схеми для великої кількості входів та виходів у вигляді єдиного блоку, зображеного на рисунку 5.2, практично неможлива. Тому в комутаційних полях комутаційні елементи об’єднані в блоки комутації, які мають обмежену кількість входів та виходів та з’єднані таким чином, щоб разом забезпечити необхідну кількість входів та виходів. Крім того, блоки комутації характеризуються тим, що з’єднання в них встановлюється по однаковим алгоритмам.

Перевагою такого способу є те, що комутаційне поле може бути побудовано з типових блоків комутації та те, що кількість точок комутації, як буде розглянуто далі, може бути значно зменшена в зрівнянні зі схемою на рисунку 5.2 (у випадку ланкового включення).

Для проведення аналізу блок комутації, який є частиною комутаційного поля, також можна представити у вигляді комутаційної схеми. І навпаки, комутаційну схему, яка відображає сутність побудови комутаційного поля можна представити у вигляді з’єднання окремих блоків комутації, які мають певні властивості.

Можливі варіанти умовного зображення блоків комутації з N входами та М виходами показані на рисунку 5.4. Позначення блоку комутації у вигляді прямокутника (рисунок 5.4, а) указує на те, що N = М. Якщо N ≠ М, то може використовуватися позначення у формі трапеції, причому більша сторона відповідає більшій кількості входів або виходів. Можливий випадок «стиску» (концентрація), коли N > М (рисунок 5.4, б) або «розширення», коли N < М (рисунок 5.4, в).

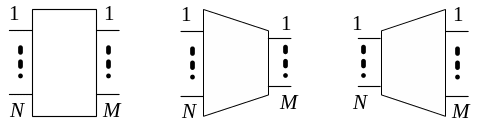
а) б) в)

Рисунок 5.4 – Умовне зображення блоків комутації

Способы искания в коммутационных полях. При установлении соединения в коммутационном поле происходит поиск свободных соединительных путей, выбор одного из них и его образование.

В коммутационных полях используют следующие способы поиска соединительных путей: свободное, групповое и линейное искания. Рассмотрим эти способы искания в случае соединения через один блок коммутации.

При свободном искании (рисунок 5.5, а) осуществляется поиск свободного соединительного пути от конкретного i-го входа блока коммутации к любому из его выходов. Например, при свободном искании в однозвенном блоке коммутации от любого входа к N выходам существуют N соединительных путей.

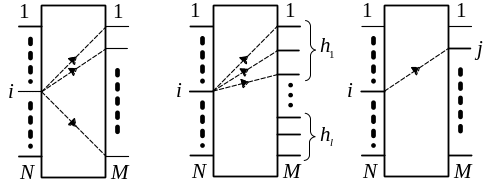
а) б) в)

Рисунок 5.5 – Свободное (а), групповое (б) и

линейное (в) искания

При групповом искании выходы блока коммутации делятся на группы (рисунок 5.5, б). При этом осуществляется поиск свободного соединительного пути от конкретного i-го входа блока коммутации к любому из выходов определенной группы. Количество групп выходов называется делимостью, а количество выходов в одной группе - доступностью коммутационного поля.

При линейном искании (рисунок 5.5, в) осуществляется поиск свободного соединительного пути от конкретного i-го входа блока коммутации к конкретному j-му выходу. Отметим, что линейное искание является частным случаем группового искания, если в каждой группе присутствует только один выход.

Блоки коммутации можно соединять параллельно и последовательно. Последовательное соединение блоков коммутации называют звеньевым включением, а коммутационные схемы, образованные звеньевым включением – многозвенными коммутационными схемами.

Параллельное соединение блоков коммутации. В случае параллельного соединения могут быть объединены входы (рисунок 5.6, а) или выходы (рисунок 5.6, б) нескольких блоков коммутации. При этом в соединении участвует одна точка коммутации. В данном случае считается, что все блоки коммутации являются полнодоступными.

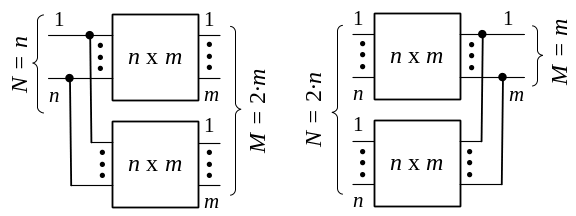
а) б)

Рисунок 5.6 – Пример объединения входов (а) и

выходов (б) блоков коммутации

Анализируя полученные коммутационные схемы, можно сделать вывод, что объединение входов приводит к образованию расширения, а объединение выходов – к образованию сжатия (концентрации).