§5.11. Перенос электрона. Электронно-конформационное взаимодействие

В химии перенос электрона между молекулами рассматривается как окислительно-восстановительная реакция (см. с. 538). С точки зрения физики перенос электрона – это электронная проводимость. В отличие от химических окислительно-восстановительных реакций в растворах, происходящих при столкновениях молекул, имеющих избыток кинетической энергии, перенос электрона между донором и акцептором в белках происходит без непосредственного контакта этих групп (на расстояниях ~10Ả), хотя перенос может идти с большой скоростью ~10¹² с^–1, близкой к частоте атомных колебаний.

Основная особенность, отличающая транспорт электронов в белках от электропроводности, например, металлов, заключается в том, что перенос электронов в макромолекулах сопровождается изменением положений ядер атомов в белковых частях акцептора электрона. Это приводит к понижению электронного энергетического уровня у акцептора, что обеспечивает эффективность переноса электрона.

При изменении электронного (химического, зарядового) состояния функциональных групп макромолекулы, энергия реакции может сразу вся израсходоваться на возбуждение колебательных степеней свободы (см. ниже электронно-колебательное взаимодействие), а может часть энергии запасаться в напряжении конформационных степеней свободы. Скорость релаксации по конформационным степеням свободы значительно меньше скорости колебательной релаксации. Однако конформационное запасание энергии открывает возможность конформационных переходов и изменения реакционной способности функциональных групп.

Существует несколько способов переноса электрона. Основным из них является туннельный перенос.

5.11.1. Электронно-колебательное взаимодействие

Туннельный перенос электрона без непосредственного контакта донора и акцептора в биополимерах может производиться на большие расстояния порядка (10÷15)Å. Эффективный перенос электрона при туннелировании не требует тепловой активации и сохраняется при очень низких температурах, включая температуру кипения жидкого гелия (Т = 4,2 К). Интересно, что даже при комнатной температуре квантово-механическое туннелирование является основным механизмом переноса в белковой среде (с донора на акцептор).

Рассмотрим, как меняется колебательный спектр ядер в донорно-акцепторном комплексе при переносе электрона. Пусть в исходном состоянии ядерные конфигурации у донора и акцептора таковы, что электрон локализован на доноре D^–, и комплекс записывается в виде . После переноса электрона комплекс переходит в состояние . При этом энергия комплекса и его пространственная конфигурация изменяются. Будем характеризовать равновесное исходное состояние обобщенной конформационной координатой R_D, определяющей некоторое эффективное расстояние между ядрами в системе, а равновесное конечное (после перехода электрона) – R_A. Зависимость потенциальной энергии комплекса от обобщенной координаты R имеет вид потенциальной ямы, аналогичной зависимости потенциальной энергии взаимодействия двух взаимодействующих частиц, как функции расстояния между ними (т.1, с.156, рис. 3–2).

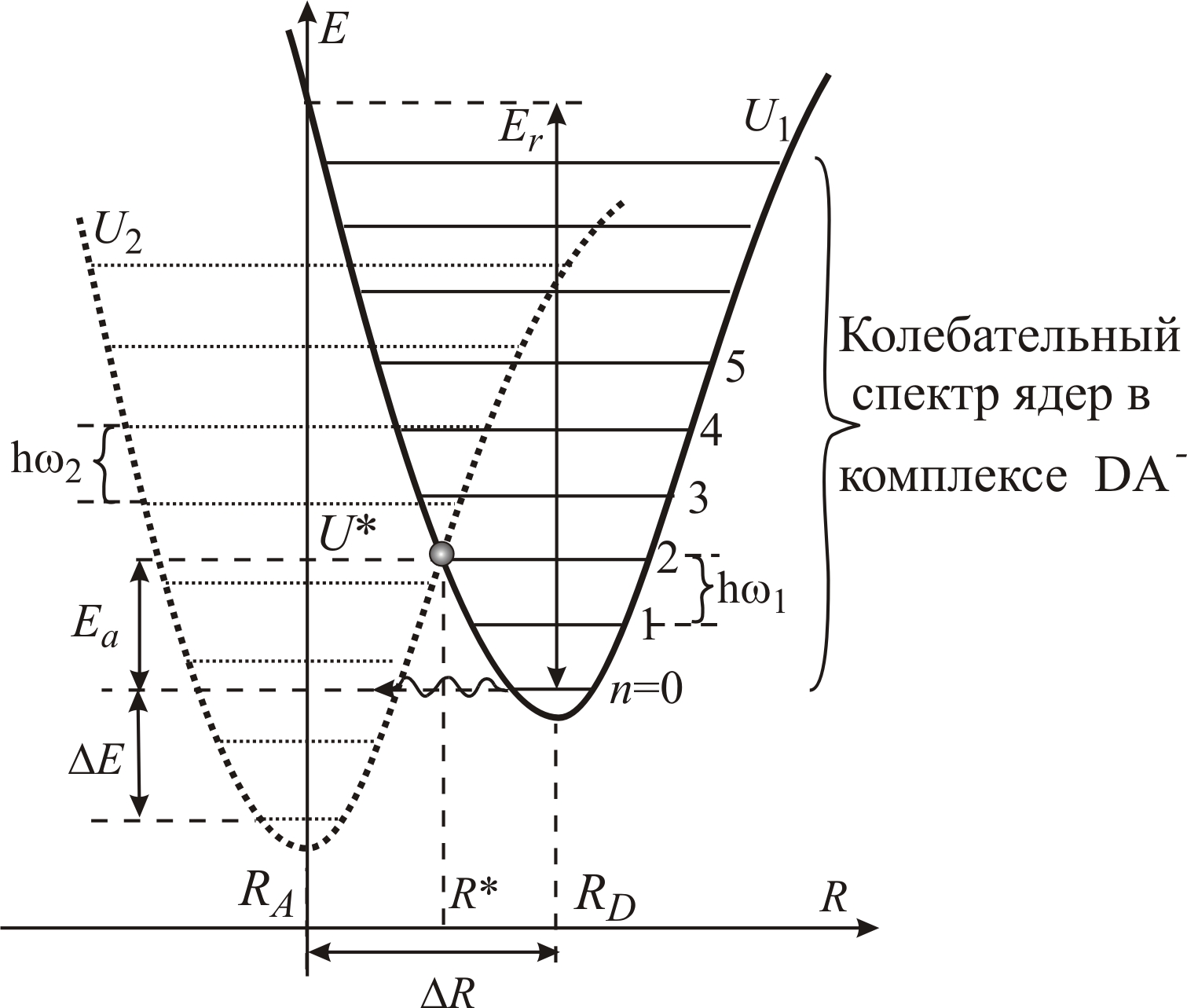
Рис. 5–26. Схема, иллюстрирующая электронно-колебательное взаимодействие при туннелировании электрона (волнистая стрелка) от донора к акцептору: U₁ и U₂ – потенциальные энергии, R_D и R_A – координаты равновесной конфигурации комплексов D^–A и DA^–, соответственно; ΔR – смещение положения равновесия ядер при изменении электронного состояния комплекса (при переходе электрона от донора к акцептору); E_a – энергия активации; ΔE – тепловой эффект реакции. E_r – энергия реорганизации системы, равная внешней работе, необходимой для сдвига координат ядер при условии, что система остается на начальном электронном терме Fe²⁺. Волнистая линия – туннелирование частиц комплекса из одного состояния в другое

Каждому состоянию и соответствуют минимумы потенциальной энергии U комплекса на графике U(R) (рис.5–26), расположенные при значениях R =R_D и R = R_А. Обе потенциальные ямы, соответствующие основным электронным состояниям и , заполнены дискретным рядом разрешенных энергетических уровней, представляющих собой квантованный колебательный спектр комплексов и . Основное равновесное состояние комплекса соответствует нижнему энергетическому уровню в потенциальной яме.

Вероятность квантово-механического перехода электрона между состояниями D^–A и DA^–, то есть частота обмена электроном между донором D и акцептором А, пропорциональна матричному элементу энергии взаимодействия:

,

где и – волновые функции электронов в комплексах и , U –потенциальная энергия взаимодействия донора и акцептора. Условие резонансного перехода сохраняется, если разность энергий начального и конечного состояний электрона удовлетворяет условию:

.

При резонансном переходе вероятность туннелирования слева направо и справа налево одинаковы, так что направленного переноса электрона из одного состояния в другое не происходит. Чтобы перенос был необратимым необходимо, чтобы за время пребывания электрона на акцепторе произошла диссипация энергии, что предотвратило бы обратный переход электрона по тому же пути к донору. Можно сказать, что закрепление электрона на акцепторе А происходит за счет потери части энергии электрона (~0,1 эВ).

Диссипация энергии означает уширение электронного энергетического уровня. Уширение уровня может произойти за счет дальнейшего туннелирования электрона в ближайшее окружение акцептора или за счет движения ядер. Последняя причина, как правило, играет основную роль.

Таким образом, необратимый переход электрона (транспорт электрона) осуществляется, благодаря перестройке ядерной конфигурации комплекса. В первый момент при переходе электрона за время (10^–12÷10^–13) сек ядра смещаются на расстояния меньше 0,1 Å в неравновесное конформационное состояние. В результате изменения заряда, состояние макромолекулы оказывается конформационно-напряженным. Малое смещение ядер индуцирует понижение энергии системы и соответственно понижение энергии электрона на акцепторе. Избыток энергии электрона переходит в тепло, увеличивая амплитуду колебаний ядер ( ), и способствует дальнейшей перестройке пространственной конфигурации комплекса в новое конформационно-равновесное состояние. Переход сопровождается смещением ядер по конформационной координате из положения R_D в положение R_A (на расстояния порядка нескольких ангстрем).

Вероятность (а, следовательно, и константа скорости) перехода D^–А→DA^– приближенно может быть представлена в виде суммы двух слагаемых, связанных с перестройкой ядерной системы: вероятности квантово-механической подбарьерной перестройки, не зависящей от температуры, и вероятности термоактивированного надбарьерного перехода ядерной системы:

. (5.47)

Здесь – вероятность надбарьерной перестройки ядер туннелирования при Т→, Е_a – энергия активации, равная разности колебательной энергии ядер E и высоты энергетического барьера: .

Термическая активация ядерной системы должна быть такой, чтобы при движении ядер достигалась точка R*. В этом случае активационная составляющая вероятности ядерной перестройки определяется фактором Больцмана , то есть величиной энергии активации . Если при движении ядер достигается точка R* (Е_а = 0) пересечения электронно-колебательных термов U₁ и U₂, в которой потенциальные энергии комплексов D^–A и DA^– одинаковы, то переход ядер происходит за время, равное периоду колебаний. При таком переходе не изменяется полная электронно-колебательная энергия системы, перестройка электронной волновой функции: D^–A ↔ DA^– происходит без дополнительной энергии. Еще раз подчеркнем, что даже при комнатных температурах термическая активация требуется только для перестройки ядерной системы, а электрон переносится с донора на акцептор туннельным путем.

Туннельное смещение ядер, аналогичное электронному туннелированию, зависит от степени перекрывания ядерных волновых функций и характерно для низких температур. Чисто безактивационное туннелирование преобладает при Т < 100 К.

Вероятность w₀ туннелирования частицы под барьером при одном столкновении с ним увеличивается при уменьшении высоты (U*–E) и ширины потенциального барьера l:

(формула Гамова),

где М – масса, Е энергия туннелирующей частицы.

При увеличении величина и ширина потенциального барьера растут. Для частиц с массой при высоте и длине барьера, соответственно, , l~1Å вероятность туннелирования близка к единице.

При туннелировании энергия частицы сохраняется. Это значит, что частица преодолевает барьер по горизонтальной линии (волнистой стрелке на рис. 5–26), соответствующей значению энергии частицы в исходном состоянии. Общее время перестройки из состояния R_D в равновесное состояние R_A составляет (10^–3÷10^–6) с.

Рис. 5–27. Зависимость логарифма скорости окисления цитохрома с в фотосинтезирующих бактериях от обратной температуры, описывающая высокотемпературную (надбарьерную) и низкотемпературную (туннельную) перестройку ядерной системы при туннелировании электрона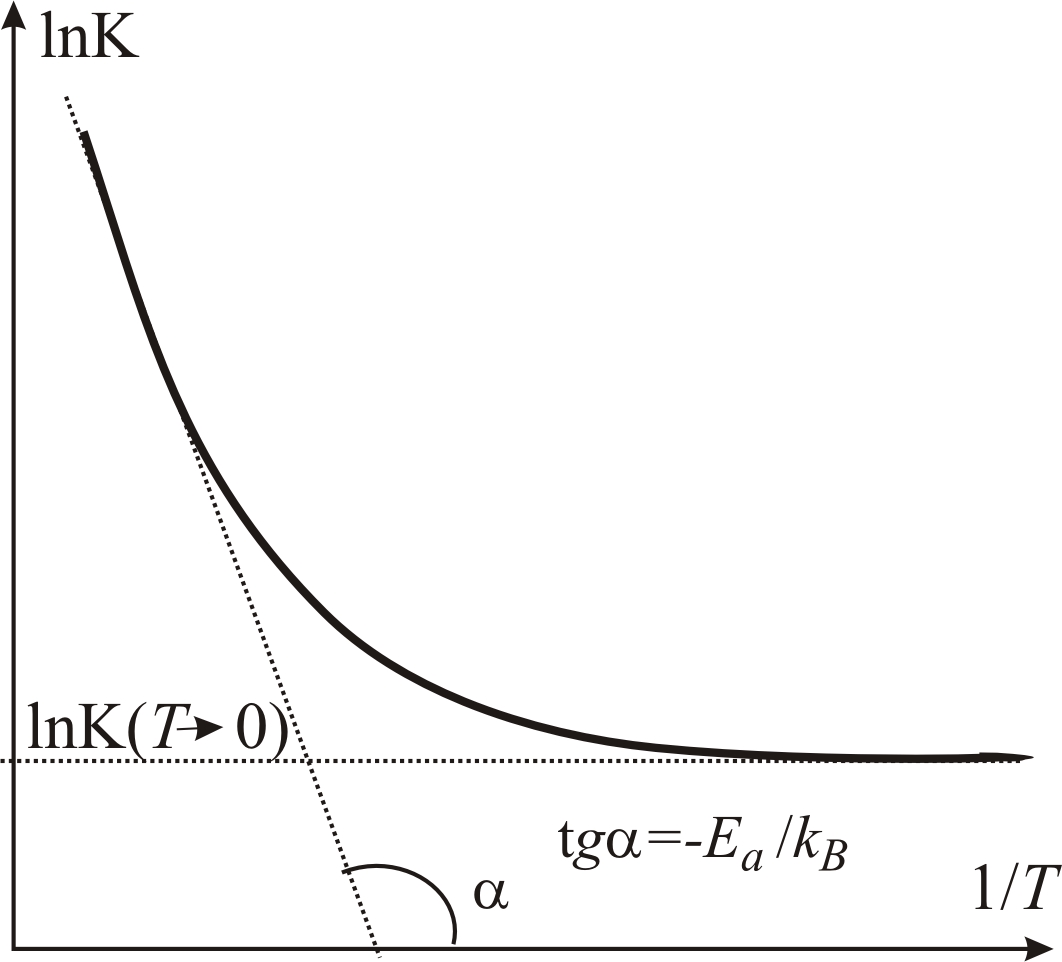

Характерный вид температурной зависимости скорости окисления гема цитохрома с (цитохромы – это группа железосодержащих белков, участвующих в переносе электронов в аэробных клетках) в белке реакционного центра фотосинтезирующих бактерий, представленный на рис. 5–27, подтверждает наличие двух различных видов функциональных зависимостей. При низких температурах скорость реакции практически не зависит от температуры, что означает наличие туннельного механизма переноса. При высоких температурах существенное влияние оказывает туннелирование электрона, сопровождаемое термоактивированной ядерной перестройкой. Тангенс угла наклона кривой позволяет определить энергию активации Е_а этого процесса, которая составляет примерно 0,1 эВ ( , l≈1,2 нм). Для порфириновых молекул при расстояниях ≤0,1 нм барьер практически отсутствует.

Таким образом, перестройка ядерной конфигурации комплекса и переход электрона – взаимосвязанные, сопряженные процессы. Сопряжение транспорта электронов в белках с перестройкой ядерной системы и диссипацией части электронной энергии называется электронно-конформационным взаимодействием. При изменении конформации белковые группы смещаются на расстояния (до нескольких десятков нм) заметно превышающие амплитуды тепловых колебаний атомов (~1 нм). Электронно-конформационное взаимодействие является основой функционирования макромолекул белков. Функциональная активность непосредственно связана с изменением электронного состояния белков, которое индуцирует определенные конформационные переходы в новые равновесные состояния, соответствующее минимумам конформационной энергии для измененных электронных состояний.