5.10.4. Модели индуктивно-резонансной миграции энергии

Как уже говорилось, индуктивно-резонансный перенос энергии может происходить как между молекулами, так и внутри одной молекулы. Если макромолекула имеет несколько степеней свободы, между которыми имеется связь, то возбуждение одной из степеней свободы приводит, благодаря наличию взаимодействия, к возбуждению других степеней свободы макромолекулы. Таким образом, связанные друг с другом степени свободы могут обмениваться энергией.

Механическая модель

Механическим аналогом, поясняющим механизм индуктивно – резонансного переноса энергии могут служить два одинаковых маятника, связанных друг с другом пружинкой (рис. 5–21): – собственная частота колебаний маятников в отсутствие связи, b₀ – коэффициент жесткости пружин маятников, m – масса маятников, b – коэффициент жесткости пружины связи (коэффициент связи). Условие слабой связи записывается в виде

. (5.27)

Уравнения движения маятников имеют вид

, (5.28)

, (5.29)

где х₁ и х₂ – смещения из положений равновесия, соответственно, первого и второго маятников (рис. 5–21).

Деля на массу и складывая уравнения (5.28) и (5.29), получаем

, (5.30)

а вычитая –

. (5.31)

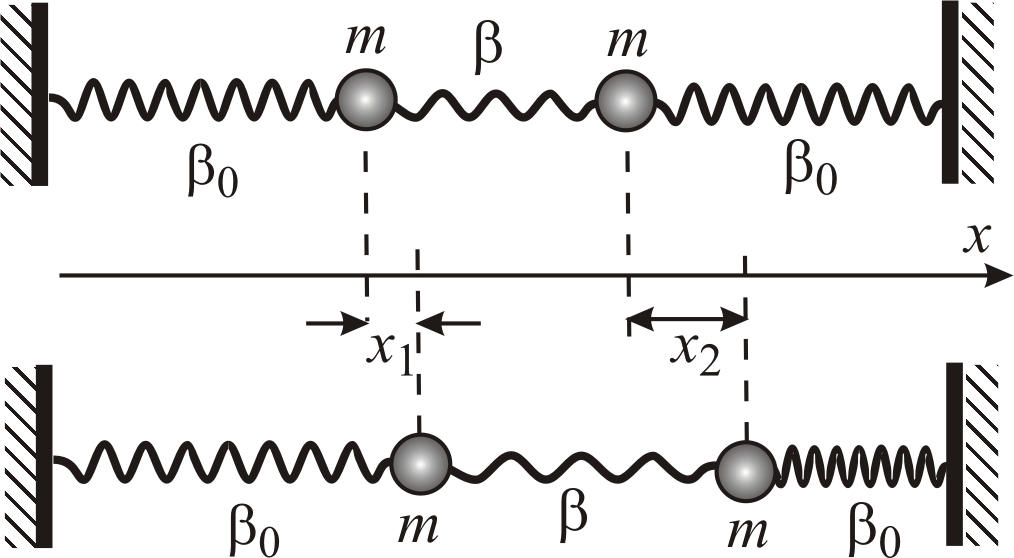
Рис. 5–21. Система двух связанных маятников с сосредоточенными параметрами (шарики с массой m не обладают упругостью, пружины с коэффициентами жесткости и невесомы). х1 и х2 – смещения из положений равновесия первого и второго шариков соответственно

Уравнения (5.30) и (5.31) представляют собой уравнения гармонических колебаний (нормальных колебаний системы связанных маятников). Общее решение уравнения (5.30) записывается в виде

(5.32)

где частота . (5.33)

Решение уравненияе (5.31) имеет вид

, (5.34)

где частота w₂ с учетом (5.27) приближенно равна

(5.35)

(5.36)

Амплитуды С₁, С₂ и начальные фазы φ₁, φ₂ определяются начальными условиями (смещениями из положений равновесия и скоростями при t = 0). Зададим начальные условия в момент времени t = 0:

, , , (5.37)

т. е. первому маятнику сообщена кинетическая энергия .

Начальные условия (5.37) определяют фазы и амплитуды колебаний: и , . Уравнения (5.32) и (5.33) принимают вид:

, (5.38)

, (5.39)

Из (5.38) и (5.39) получаем законы движения маятников

, (5.40)

. (5.41)

и, используя, выражения для их Кинетическая энергия движения маятников, с учетом (5.35), описывается выражениями (рис. 5–22):

, (5.42)

. (5.43)

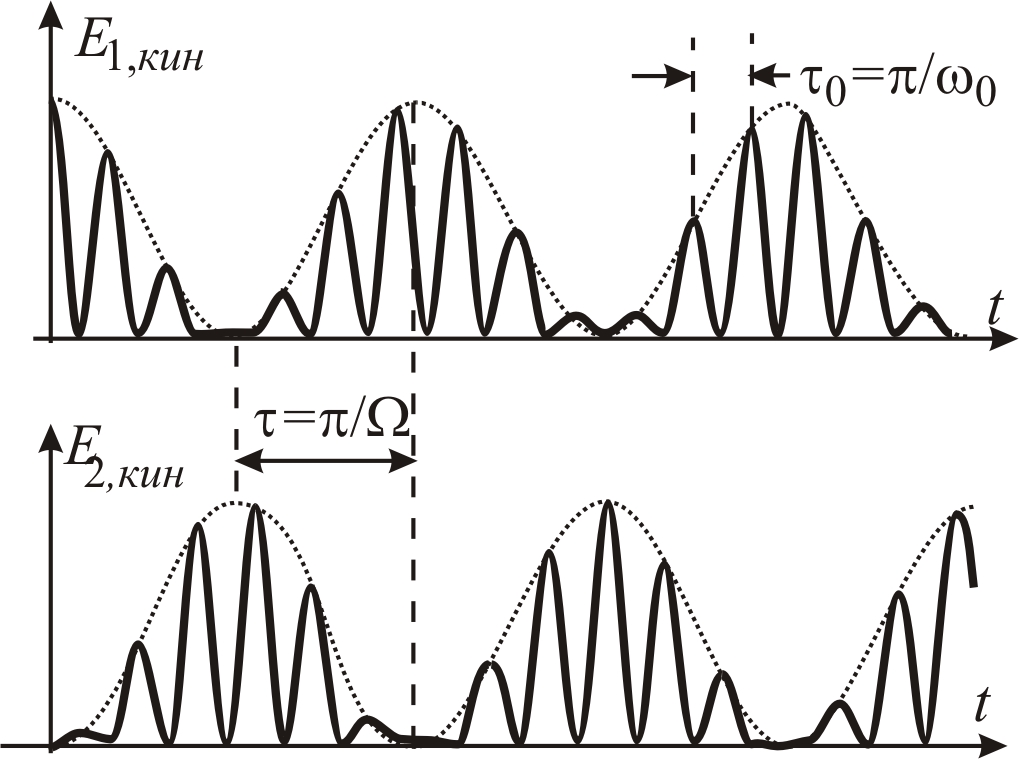
Рис. 5–22. Зависимости от времени кинетических энергий и первого и второго маятников; — период изменения полной энергии каждого маятника (время перехода энергии из кинетической в потенциальную и обратно); – время перекачки энергии от одного маятника к другому

Из рис. 5–22 видно, что, во-первых, кинетическая энергия каждого маятника периодически с частотой 2w₀ (периодом ) переходит из кинетической в потенциальную и обратно и, во-вторых, – через время происходит перекачка энергии от одного маятника к другому. Процесс обмена энергиями между маятниками полностью обратим. Если в рассматриваемой системе учесть возможную диссипацию энергии, то обмен энергиями будет происходить с частотой до тех пор, пока колебания не затухнут.

Аналогичный результат можно получить для двух связанных молекулярных осцилляторов. Поскольку процесс переноса энергии между двумя одинаковыми молекулами в стационарных условиях является обратимым, то он не приводит к направленному переносу энергии, а может приводить лишь к ее миграции от одной молекулы к другой.