18.6.3. Методи врахування складних природних і меліоративних умов в розрахункових схемах прогнозу

Схематизація складних геометричних границь пластів. Реальний криволінійний контур області фільтрації може бути приведений до типової розрахункової схеми, наприклад, напівобмеженого пласта з прямокутною зрошуваною ділянкою (див. рис. 18.4, а). Два можливих варіанта такої схематизації криволінійної границі пласта наведені на рис. 18.11.

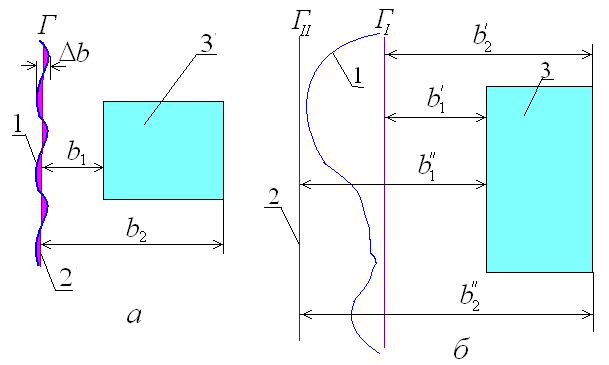
Рис. 18.10. Варіанти розрахункової схематизації криволінійного граничного контуру області фільтрації: 1 – реальний граничний контур; 2 – схематизована границя; 3 – зрошуваний масив.

Перший варіант застосовують при невеликій глибині звистості існуючого граничного контуру (рис. 18.10, а). Прямолінійна розрахункова границя пласта Г проводиться таким чином, щоб площі, що відсікаються нею, і відповідно доповнюючи криволінійних приграничних ділянок області фільтрації приблизно були рівними. При цьому відхилення розрахункового положення границі від дійсного її контуру повинні бути невеликими в порівнянні з відстанями до ділянки інфільтрації: .

Якщо даний критерій не витримується і ширина смуги, всередині якої розташований дуже звивистий граничний контур пласта, порівняний з відстанню до зрошуваної ділянки, рекомендується другий варіант схематизації (рис. 18.10, б). прямолінійні границі цієї смуги Г_І і Г_ІІ приймають як граничне положення розрахункового граничного контуру пласта по відношенню до ділянки інфільтрації: з найбільшим віддаленням від нього. Це визначає два граничних варіанта координат ділянки ( і ), що відміряють відповідно від Г_І і Г_ІІ. Аналогічним чином координата кожної розрахункової точки має два екстремальних значення: і .

В зв’язку з цим, задача прогнозної оцінки підвищення рівня ґрунтових вод в будь-якій точці області правіше Г_І зводиться до розрахунку відповідно типової схеми на рис. 18.3, а, при двох поєднаннях координат вершин зрошуваної ділянки ( , і , ), а також даної точки ( і ), що дає результати відповідно і . Шукане значення знаходиться в діапазоні між обчисленими граничними значеннями і .

У випадку великої звистості берегової лінії річок і водосховищ з граничними умовами першого і третього роду прогнозна оцінка виражається нерівністю . Розрахунки величин і виконують за рівнянням (18.64) при (гранична умова першого роду) або за іншими рівняннями.

Вказані граничні оцінки нерідко можуть бути практично достатніми для того, щоб прийти до висновку про можливість підтоплення даної території або навпаки (враховуючи особливості рельєфу місцевості). Якщо така оцінка не дозволяє дати певний прогноз через значні відмінності екстремальних значень і , необхідно використовувати в якості найбільш вірогідного їх середнього значення:

.

Показані на рис. 18.10 варіанти схематизації криволінійної границі пласта можна застосовувати і у випадках приведення до інших планових схем області фільтрації (пласт-квадрант, пласт-смуга і т. д.). При великих об’ємах розрахунків за відповідними рівняннями для прогнозної оцінки всі обчислення необхідно виконувати на ЕОМ.

Схематизація складних контурів зрошуваних масивів. Для забезпечення достовірності прогнозу практично важливо враховувати в розрахунках складну геометрію контурів зрошуваних масивів і нерівномірність розподілу інтенсивності іригаційної інфільтрації по площі території. Зрошувальна система може включати ту або іншу кількість довільно розташованих зрошуваних ділянок, розділених між собою незрошуваними площами. Інтенсивність іригаційної інфільтрації на окремих ділянках нерідко неоднакова через різний поливний режим, різні гідрофізичні властивості ґрунтів зони аерації, неоднаковий характер рельєфу місцевості та за іншими причинами.

В даному складному випадку для напівобмеженої області фільтрації можлива розрахункова схема, показана на рис.18.11. Кожна окрема зрошувана ділянка з номером і представляє прямокутник і характеризується своїм кутом нахилу відносно прямолінійної границі пласта і значенням інтенсивності інфільтрації . Вісь суміщають з границею пласта, а ортогональна їй вісь проведена нижче всіх ділянок інфільтрації.

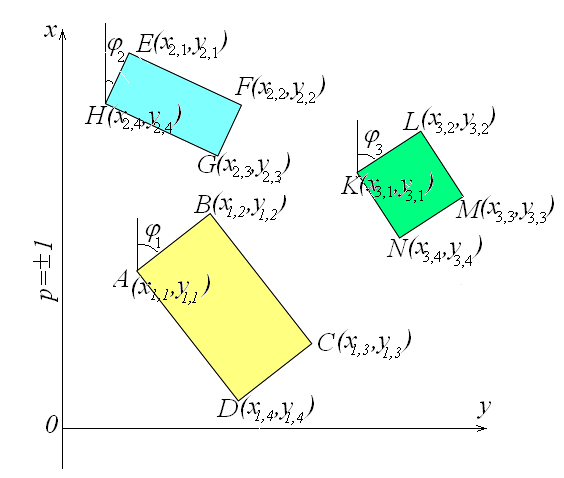
Рис. 18.11. Схема окремих прямокутних зрошуваних ділянок, довільно розташованих відносно границі пласта.

Величина результуючого підвишення рівня ґрунтових вод в кожній точці області з координатами на будь який строк прогнозу при одночасному сумісному впливі системи ділянок іригаційної інфільтрації виражається згідно принципу суперпозиції рівнянням

, (18.107)

де , , …, – часткові прирости рівня за рахунок диференційного впливу окремих зрошуваних ділянок з номером відповідно 1, 2, …, n;

– загальна кількість всіх ділянок інфільтрації.

При наявності перетікання через слабопроникний підстилаючий шар кожну із вказаних складових частин величини необхідно розглядати за рівнянням (18.96), задаючись відповідними значеннями , і координат вершин зрошуваних ділянок.

Інший практично актуальний спосіб схематизації реальної геометричної форми зрошуваних масивів показаний на рис. 18.12. Складний плановий контур ділянок інфільтрації для потреб прогнозу величини зручно представити відповідним поєднанням декількох розрахункових фрагментів – прямокутних, а іноді і трикутних фігур. При цьому очікуване підвищення рівня ґрунтових вод в будь-якій точці території визначається по принципу суперпозиції як суму часткових приростів рівнів за рахунок впливу зрошення на кожному із вказаних фрагментів.

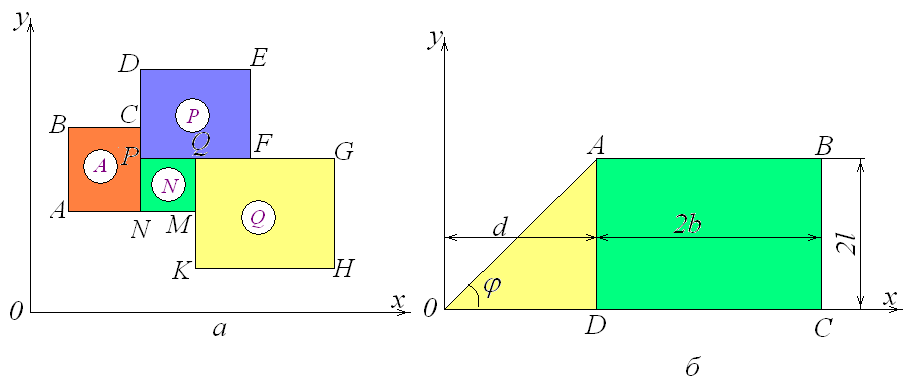
Рис. 18.12. Фрагментування зрошуваних масивів складної геометричної форми: а – поєднання прямокутних фігур; б – поєднання трикутних і прямокутних фігур.

Рис. 18.13, а ілюструє приклад розташування в пласті-квадранті зрошуваної площі, що має складний ступінчастий контур ABCDEFGHKM, ортогональні відрізки якого паралельні координатним осям і , суміщеним з границями пласта. Для зручності розрахунку ця фігура розділена на фрагменти: прямокутники ABCN, PDEF, NPQM i QGHK (як один із варіантів). Фрагменти позначені символами A, P, N i Q.

Прогнозна величина підйому ґрунтових вод , що викликаний іригаційною інфільтрацією інтенсивністю на всій площі масиву ABCDEFGHKM, виражається сумою

, (18.108)

де , , , – часткові прирости рівня ґрунтових вод за рахунок диференційованого впливу зрошення на прямокутних фрагментах відповідно A, P, N i Q.

Формулу (18.108) можна застосовувати до всіх точок масиву і прилеглої незрошуваної території на будь-який строк прогнозу.

Другий приклад фрагментування, наведений на рис. 18.12, б, відноситься до зрошуваних площ з ломаним контуром. Масив, що має форму трапеції ОАВС, розбивається на два розрахункових фрагменти: трикутник OAD і прямокутник ABCD. Довжини відрізків OD, AB i BC дорівнюють відповідно d, 2b i 2l. Сторони трикутника ОА і ОD утворюють кут в діапазоні від 0 до . Пласт є умовно однорідним на водоупорі і розглядається як необмежений в плані. Початок координат суміщається з вершиною трикутника О, а вісь Ох – з основою трапеції. Розрахункова залежність для прогнозу підйому ґрунтових вод , що викликаний іригаційною інфільтрацією на площі трапецієподібного масиву ОАВС, має вигляд [31руд]:

, (18.109)

де І – функція (18.57) при аргументах і ;

– функція (18.61) з аргументами ;

, , , ,

, , , ,

, .

Врахування коливань інтенсивності іригаційної інфільтрації за часом. Основні способи розрахункової схематизації складної зміни за часом величини і умов їх застосування охарактеризовані в п. 18.2.2. У випадку використання для прогнозу величини ступінчастого графіка , тобто схеми стрибкоподібної зміни інтенсивності іригаційної інфільтрації (див. рис. 18.1, б), рівняння викликаних ними коливань рівня ґрунтових вод має вигляд при :

, (18.110)

де – відповідне аналітичне рівняння відносної величини підйому рівня ґрунтових вод (при ).

Це рівняння, ґрунтується на принципі суперпозиції, дійсне для всіх розглянутих в п. 18.5.1 і 18.5.2 розрахункових схем форми і розташування зрошуваних площ, форми пласта і типу граничних умов, структури області фільтрації (умовно однорідний пласт на водоупорі, перетікання через слабопроникний підстилаючий шар, планова неоднорідність водоносної товщі на водоупорі). Його можна застосувати і при будь-якій апроксимації складної геометрії границь пластів і контурів зрошуваних масивів. Тому при розрахунках за рівнянням (18.110) можуть бути використані в якості всі наведені вище розрахункові залежності при (вважаючи ).

Викладене вище можна показати на прикладі прямокутного зрошуваного масиву в необмеженому умовно однорідному пласті на водоупорі (див. рис. 18.2, а). Визначають очікуване коливання рівня ґрунтових вод в центральній точці ділянки 1. Підставляючи в рівняння (18.115) вираз згідно формулі (18.53) при і=1 і , отримують конкретну розрахункову залежність для п-ї ступені графіка :

, (18.111)

де , , ,

; .

Розрахунки за цією залежністю виконують за допомогою інтерполяції табличних значень функції І, застосовуючи в якості аргументів і їх значення, вказані в формулі. Залежність (18.111), як і загальне рівняння (18.110), може бути використане при будь-якій ступені графіка .

Для короткострокових прогнозів зміни рівня ґрунтових вод функцією доцільно представити у вигляді лінійної залежності: при (див. 18.1, г). Стосовно до схеми прямокутної ділянки в необмеженому пласті (див. рис. 18.2, а) рівняння для розрахунку прогнозної величини в період часу має вигляд:

, (18.112)

де

; (18.113);

, ; , ;

– початкове значення в момент , м/добу;

– уклон лінійного графіка ;

інші позначення ті ж, що в рівнянні (18.60).

Для прогнозних розрахунків величини в напівобмеженому пласті з прямокутною зрошуваною ділянкою (див. рис. 18.3, а) при лінійній залежності необхідно перетворити рівняння (18.64) в такому порядку: виключити множник перед фігурною дужкою, а замість кожного члена рівняння підставити відповідний вираз

,

де , ; ;

.

Схема кусочно-лінійної залежності (див. 18.1, д) дозволяє найбільш детально враховувати при прогнозуванні величини безперервний хід зміни за часом інтенсивності інфільтрації . В якості приклада можна навести відповідну цій схемі розрахункову формулу очікуваної зміни рівня для центральної точки 1 прямокутної зрошуваної ділянки в необмеженому умовно однорідному пласті на водоупорі (див. рис. 18.2, а) при :

, (18.114)

де – значення уклону 1, 2, 3-ї, … (п-1)-ї, п-ї гілки ломаного графіка в періоди часу відповідно , , , …, , ;

– коефіцієнти, що мають ті ж вирази, що і в формулі (18.111), м^-1;

смисл інших позначень такий же як у попередньому викладі.