18.6.1. Розрахунки підвищення рівня ґрунтових вод при зрошенні в умовно однорідному пласті на водоупорі

Необмежений в плані пласт. Цю модель необхідно застосовують в тих випадках, коли зовнішні границі області фільтрації настільки віддалені від зрошуваного масиву, що плив зрошення практично не досягає їх за розрахунковий період часу. Типові геометричні форми зони іригаційної інфільтрації в такій області представлені на рис. 18.2.

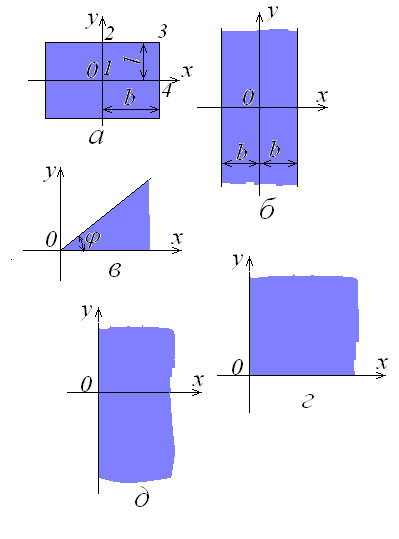
Рис. 18.2. Типові форми зони іригаційної інфільтрації в необмеженому пласті.

Основна розрахункова схема – прямокутна ділянка інфільтрації з будь-яким співвідношенням довжин його сторін і (див. рис. 18.2, а).

Прогнозне підвищення рівня ґрунтових вод при розраховують за рівнянням

, (18.56)

де – координати розрахункової точки планової області, м;

– розрахункова інтенсивність іригаційної інфільтрації, м/добу;

– тривалість прогнозного періоду, діб;

– коефіцієнт гідроємкості ґрунту в зоні аерації;

; (18.57)

; ;

, , , ;

– геометричні параметри ділянки інфільтрації, м;

– коефіцієнт рівнопровідності пласта, м²/добу.

Функція введена і табульована [рудаков]. Значення для практичного використання застосовують у табличній формі.

В характерних точках 1-4 зрошуваної ділянки (див. рис. 18.2, а) зручніше знаходити за спрощеною формулою

, (18.58)

де – числові коефіцієнти, що залежать від номера точки і: при і=1; при і=2; приі=3; при і=4;

; .

Максимум підвищення рівня відбувається в центрі цієї ділянки (точка 1). Процес підйому рівня при не припиняється з часом і може наближатись до поверхні землі, призводячи до підтоплення території

Для розрахунку в середній частині витягнутої в плані прямокутної ділянки інфільтрації зручно користуватись схемою смугової інфільтрації (див. рис. 18.2, б). В цьому випадку можна вважати, що рівень ґрунтових вод буде змінюватись тільки в одному напрямку – х. Розрахункова формула має вигляд

, (18.59)

де – відома спеціальна табульована функція [рудак];

інші позначення ті ж.

У випадку кутової зони інфільтрації (рис. 18.2, в) необхідно змінити формулу

, (18.60)

де

; (18.61)

; ; ; ; ;

– кут зони може бути в діапазоні від 0 до .

Функція введена і табульована, окремо представлені графіки її при [ ]. Якщо , . Величина знаходиться за таблицями значень функції , вважаючи , .

Коли кутова зона інфільтрації представляє квадрант (рис. 18.2, г), тобто , формула для розрахунку має вигляд

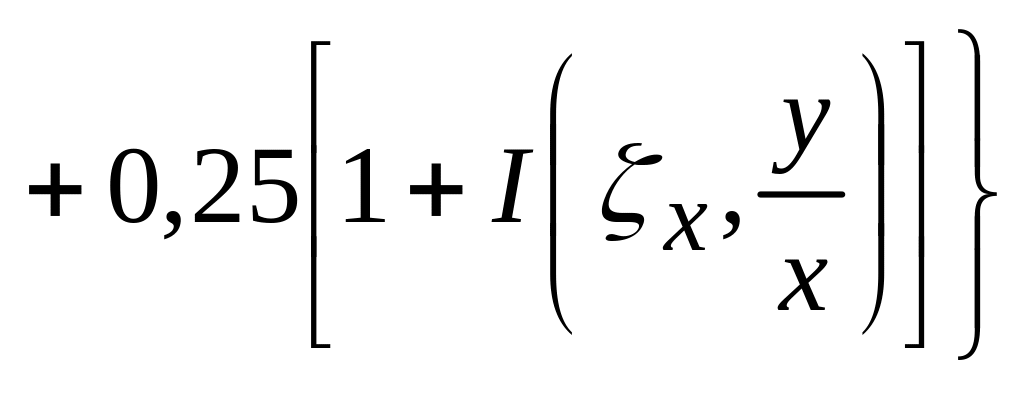. (18.62)

Для точок, розташованих близько одного краю зрошуваного масиву, можна застосувати схему інфільтрації півплощині (рис. 18.2, д) за формулою

. (18.63)

Напівобмежений пласт. Якщо підвищення рівня ґрунтових вод розповсюджуються від зрошуваного масиву до зовнішньої границі області, необхідно переходити до схеми напівобмеженого пласта (рис. 18.3).

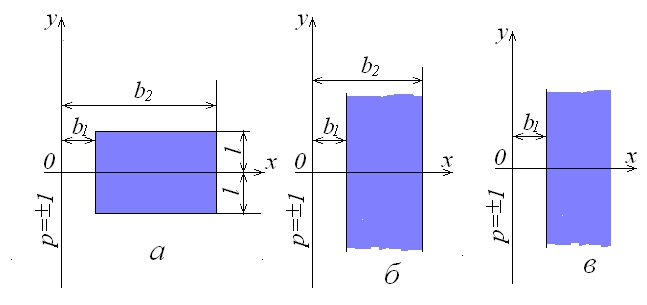
Рис. 18.3. Розрахункові форми і розташування зони іригаційної інфільтрації в напівобмеженому пласті.

Основна розрахункова схема (рис.18.3, а) – це прямокутна ділянка інфільтрації, два боки якої паралельні границі пласта . Вісь проведена через центр ділянки. Співвідношення довжин його сторін може бути будь-яким. прогнозне підвищення рівня ґрунтових вод при розраховують за формулою

, (18.64)

де , ; ;

; ; ; ;

;

– числовий коефіцієнт, що залежить від типу граничної умови на границі пласта ;

– координати кутових точок ділянки інфільтрації, м;

інші позначення ті ж.

Коефіцієнт для проникної границі з заданим рівнем (або розподіленим рівнем) води, тобто при граничній умові першого роду (наприклад, уріз водойми з фіксованим рівнем, днище яру чи балки). У випадку непроникної границі пласта (гранична умова другого роду, наприклад, водонепроникний корінний берег, скеля) коефіцієнт .

Рівняння (18.64) дійсне для всіх точок ділянки інфільтрації і прилеглої незрошуваної території. Результати розрахунків симетричні відносно осі .

Ізолінії , постійні згідно розрахункам за рівнянням (18.64) на будь-який строк прогнозу , концентрично огинають ділянку фільтрації, але мають асиметричний характер за рахунок впливу границі пласта . При ці ізолінії перетинаються по нормалі з вказаною границею, а у випадку огинають її.

При процес підвищення рівня ґрунтових вод може продовжуватись необмежено довго, наближуючись до поверхні землі і викликати підтоплення відповідної території. У випадку цей процес затухає з часом і прогнозована величина асимптотично прагне до кінцевого (граничного з часом) значення . Розрахунок для планової схеми на рис. 18.3, а виконується за рівнянням

, (18.65)

де

; (18.66)

– коефіцієнт водопровідності пласта, м²/добу;

інші позначення ті ж, що в рівнянні (18.64).

Функція введена і табульована для зручності розрахунку [ ]. Розрахунок дозволяє виявити потенційно підтоплені ділянки розглянутої території, де необхідна оцінка строків розвитку підтоплення за допомогою рівняння (18.64).

При великій витягнутості зрошуваної ділянки паралельно осі – – доцільно користуватись схемою смугової інфільтрації (рис. 18.3, б) і застосовувати замість рівняння (18.64) формулу

. (18.67)

Схема смугової інфільтрації може бути замінена більш простою схемою інфільтрації на напівлощині (рис. 18.3, в), якщо . Тоді замість формули (18.67) можна застосувати залежність

. (18.68)

Часто в районах зрошення границі з заданими рівнями води відрізняються суттєвою гідродинамічною недосконалістю і характеризуються граничними умовами третього роду (див. п. 18.5.2.). Ступінь цієї недосконалості кількісно виражається питомим контактним фільтраційним опором , доба/м на 1 м довжини границі [руданов].

Пласт-кут. До цього типу пласта відносять області фільтрації, що утворені двома перетинаючими границями з граничними умовами першого, другого або третього роду. Якщо утворений ними кут дорівнює область фільтрації представляє пласт-квадрант (рис. 18.4).

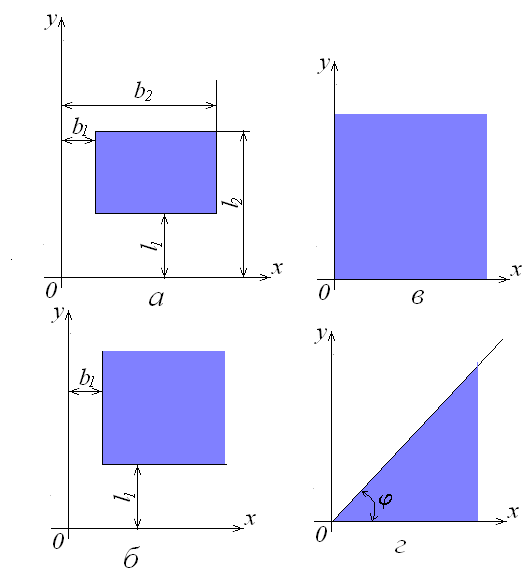
Рис. 18.4. Розрахункові схеми зони іригаційної інфільтрації в кутових областях фільтрації.

Осі і суміщають з схематизованими прямолінійними границями пласта-квадранта. Основна розрахункова схема (рис. 18.4, а) – це прямокутна ділянка іригаційної інфільтрації з будь-яким співвідношенням сторін, які попарно паралельні границям пласта.

Рівняння для прогнозу підвищення рівня ґрунтових вод при має вигляд:

, (18.69)

де ; ; ;

; ; ;

– чисельні коефіцієнти, що залежать від типу граничної умови на границях пласта відповідно при і ;

– координати кутових точок ділянки інфільтрації, м;

інші позначення ті ж, що в рівнянні (18.64)

Коефіцієнт або приймає значення –1, якщо відповідна границя має граничні умови першого роду, і значення, рівне 1, – при її непроникності (граничні умови другого роду).

Розрахунки інтерполяцією табличних значень трудомісткі і тому доцільні при малій кількості розрахункових точок. У випадку необхідності прогнозу для великої кількості точок території необхідно здійснювати на ЕОМ весь об’єм розрахунків, включаючи обчислення конкретних значень інтеграла , що входять в нього, за допомогою стандартних підпрограм математичного забезпечення.

При процес підйому рівня відбувається до часу, що наближається до поверхні землі і призводить до підтоплення даної території. Якщо , або , , цей процес буде затухати, асимптотично наближуючись до кінцевих значень підйому рівня . У випадку затухання процесу йде бистріше, знижується величина , що зменшує можливість підтоплення території.

Рівняння для розрахунку за схемою наведеній на рис. 18.4, а, при має вигляд

, (18.70)

де – функція (18.66) з аргументами

значення яких ті ж, що і в рівнянні (18.69).

Процедура розрахунків суттєво спрощується з переходом до схеми інфільтрації на внутрішньому квадраті (див. рис. 18.4, б), що допустимо при дотриманні нерівності , де – відстань від кутової точки зрошуваного масиву з координатами до його центра. У випадку розрахунок виконують за формулою

, (18.71)

де позначення ті ж, що і в рівнянні (18.69).

Якщо контуру кутової зони інфільтрації співпадають з границями пласта-квадранта (див. рис. 18.4, в) і , розрахункова формула має вигляд:

. (18.72)

Крім пласта-квадранта застосовують схему пласта-кута при . Відповідні методи розрахунку представлені в роботі [32 рудаков]. На рис. 18.4, г показана одна із таких схем: суцільна інфільтрація в пласті-куті з граничними умовами першого роду на обох границях, що утворюють кут . Розрахункова формула має вигляд:

, (18.73)

де – функція (18.64), що визначеється за спеціальними графіками наведеними в [рудаков];

Пласт-смуга. Область фільтрації представляє в плані смугу між паралельними границями з граничними умовами першого, другого або третього роду (рис. 18.5). Область такого типу – це зрошувані ділянки на міжріччі, територіях між річкою або водосховищем і магістральним каналом, між двома глибокими балками і т.д. Однією із границь може служити контур річної тераси, що складений практично водонепроникними породами цоколя плато.

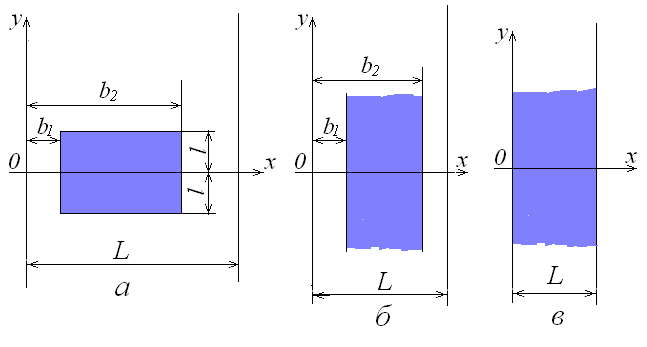
Рис. 18.5. Схеми до розрахунку підйому ґрунтових вод при зрошенні в пласті-смузі.

Вісь суміщають з лівою границею пласта. Основна розрахункова схема (рис. 18.5, а) – прямокутна ділянка інфільтрації з будь-яким співвідношенням довжин сторін, дві із яких паралельні границям пласта. Вісь проведена через центр ділянки. Рівняння для розрахунку при має вигляд

, (18.74)

де – відстань між границями пласта, м;

при граничних умовах першого роду на обох границях пласта;

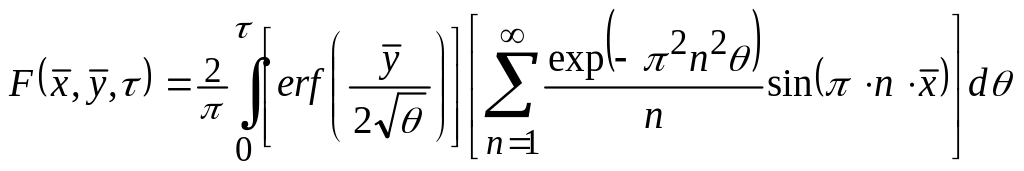; (18.75)

при непроникності границь і граничній умові першого роду на границі

; (18.76)

; ; ; ;

– координати кутових точок ділянки інфільтрації, м;

– тривалість прогнозного періоду з початку дії іригаційної інфільтрації, діб.

Функції і введені і табульовані [руд]. Результати розрахунків симетричні відносно осі . Розрахункові ізолінії величини на різні строки прогнозу концентрично огинають в плані зрошуваний масив і витягуються вздовж границь пласта з граничними умовами першого роду, але перетинаються по нормалі з непроникною границею.

Процес підйому рівня ґрунтових вод затухає з часом; величина зі збільшенням асимптотично прагне до кінцевого значення , що характеризується гранично можливим підвищенням рівня ґрунтових вод.

Розрахунки для планової схеми на рис. 18.5, а можуть виконуватись за формулами:

• при граничних умовах першого роду на обох границях пласта

, (1877)

• при непроникній границі і граничній умові першого роду на границі

, (18.78)

де ті ж, що в рівнянні (18.74).

Функції і введені і табульовані в роботах [руд].

Методика розрахунку значно спрощується з переходом від схеми прямокутного зрошуваного масиву до схеми смугової інфільтрації (див. рис. 18.5, б), що допустимо при . Тоді замість рівняння (18.74) можна застосувати формулу

, (18.79)

де – граничне за часом підвищення рівня ґрунтових вод, м;

при заданих рівнях води на обох границях пласта;

при непроникній границі і заданому рівні води на границі ;

позначення і ті ж, що і в рівнянні (18.74).

Розрахунок при першому варіанті граничних умов здійснюють за формулами:

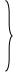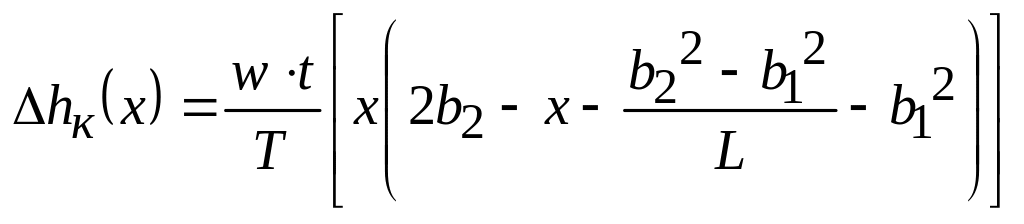при ;

при ; (18.80)

при .

У випадку другого варіанта граничних умов розрахунок виконують за формулами:

при ;

при ; (18.81)

при .

Функції і введені і табульовані [руд].

У випадку суцільної інфільтрації в межах пласта-смуги (див. рис. 18.5, в) формула для розрахунку має вигляд:

• при першому варіанті граничних умов

; (18.82)

• при другому варіанті граничних умов

, (18.83)

де , ; .

Граничні умови третього роду для пласта-смуги пов’язані в загальному випадку з гідродинамічною недосконалістю обох границь з різними значеннями параметра : на границі і на границі . Аналітичний розрахунок для прогнозу величини в цих умовах при інфільтрації на прямокутній ділянці (див. рис. 18.5, а) виконують за методикою, викладеною в роботі [34руд]. Всі обчислювальні операції при використанні даної методики необхідно виконувати на ЕОМ.

Пласт-напівсмуга. Область такого типу відрізняється від пласта-смуги наявністю третьої границі, перпендикулярної двом паралельним граничним контурам (18.6). Ця границя також може характеризуватись граничними умовами першого, другого або третього роду. Характерними прототипами пласта-напівсмуги є: територія, обмежена річкою (водосховищем) і двома паралельними її притоками; ділянку між двома паралельними горизонтальними дренами, що впадають в основний дренажний колектор.

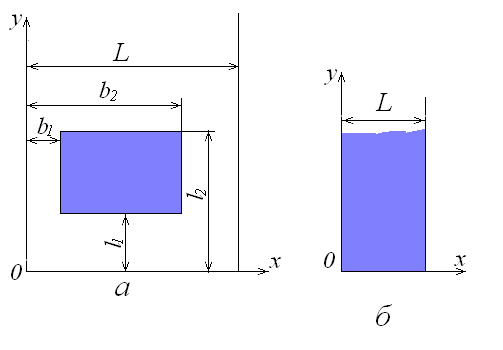
Рис. 18.6. Схематизація зони іригаційної інфільтрації в пласті-напівсмузі.

Осі і суміщають з лівою границею пласта і перпендикулярною їй границею. В основній розрахунковій схемі ділянка іригаційної інфільтрації не примикає до границь пласта і має форму прямокутника з будь-яким співвідношенням довжин сторін, дві із яких паралельні осі , а дві інші – осі (див. рис. 18.6, а). Рівняння для розрахунку при має вигляд:

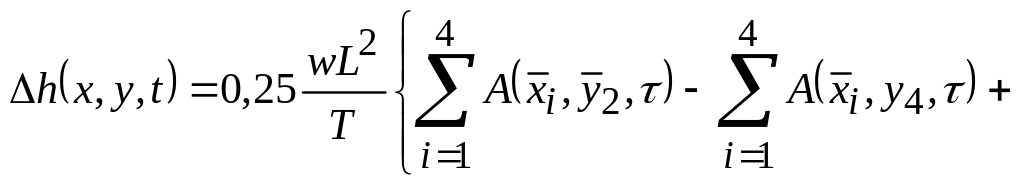
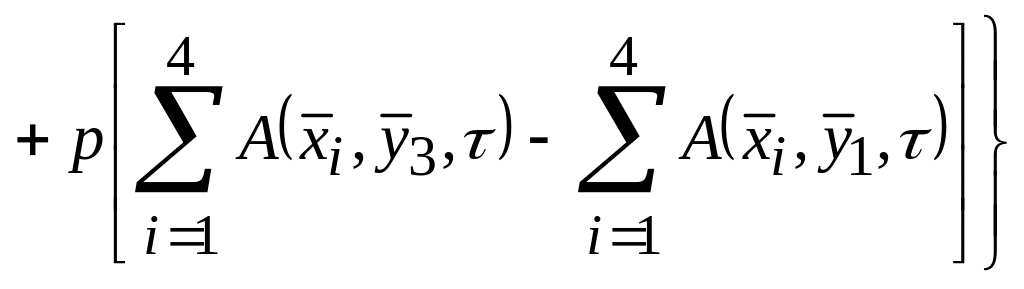, (18.84)

де , , , ;

– координати кутових точок ділянки інфільтрації, м;

всі інші позначення ті ж, що в рівнянні (18.74).

Коефіцієнт приймає значення –1 і 1 при граничній умові відповідно першого і другого роду на границі . Використовуючи поряд з коефіцієнтом функції і , що виражаються інтегралами (18.75) і (18.76), можна враховувати за допомогою рівняння (18.84) будь-які комбінації граничних умов першого та другого роду на границях пласта-напівсмуги.

У випадку суцільної інфільтрації по площі пласта-напівсмуги (рис.18.6, б) розрахункова формула має вигляд:

• при граничних умовах першого роду на всіх границях пласта

; (18.85)

• при непроникних границях і граничних умовах першого роду на границях і

, (18.86)

де , ; .

Пласт-прямокутник. Область фільтрації замкнута прямокутним контуром із чотирьох взаємно перпендикулярних границь. Такий тип області застосовують в районах зрошення з розвинутою гідрографічною, іригаційною і дренажно-колекторною мережею (рис. 18.7).

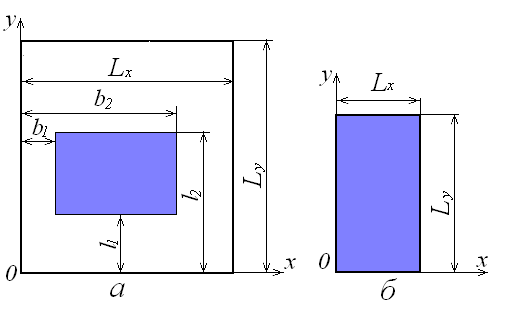
Рис.18.7. Схематизація зони іригаційної інфільтрації в пласті-прямокутнику

В загальній розрахунковій схемі (рис. 18.7, а) область фільтрації прямокутники з будь-якими співвідношеннями сторін. Контури і центри цих прямокутників можуть не співпадати, сторони їх взаємно паралельні.

Рівняння для прогнозу підвищення рівня ґрунтових вод в такій області з граничними умовами першого роду на всіх границях виведені в роботі [30 руд]. Весь об’єм обчислених операцій при використанні даного рівняння доцільно виконувати на ЕОМ.

Якщо границі ділянки інфільтрації і пласта-прямо­кут­ни­ка співпадають (рис. 18.7, б), величину підйому рівня на цій території при і заданих граничних рівнях води можна виразити формулою

, (18.87)

де

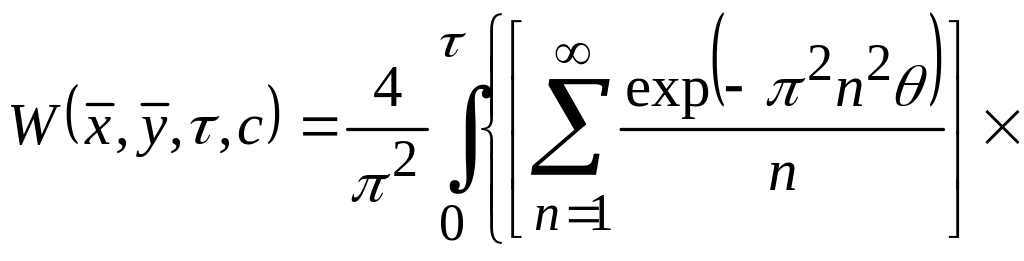
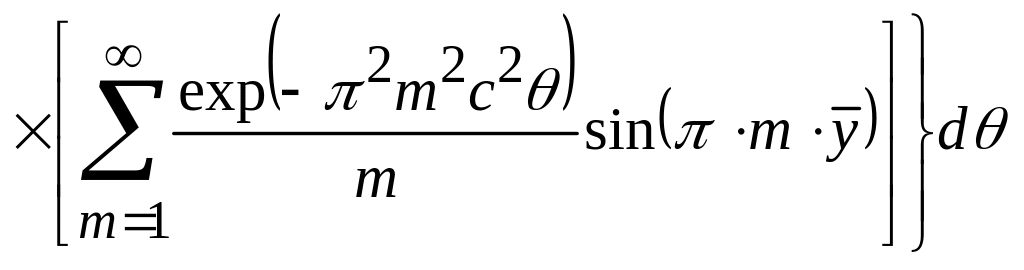; (18.88)

; ; ;

; ;

– лінійні розміри області фільтрації, м.

Максимальне підвищення рівня приурочене до центру ділянки ( ; ) і може бути розраховано за формулою

(18.89)

Функція введена і табульована [30].