3. Расчет зубчатых передач на контактную прочность.

Проверочный расчет на контактную прочность при перегрузках. В этом слу­чае при действии максимальной на­грузки Т_1mах

Наибольшее в течение заданного срока службы контактное напряжение определяют по формуле

где K_Hmax — коэффициент нагрузки, определяе­мый при T_max.

Д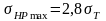 опустимое предельное напряжение σ_HPmax принимают в зависимости от способа химико-термической обработ­ки зубчатого колеса. Так, для зубчатых колес, подвергнутых нормализации, улучшению, объемной закалке,

д ля зубьев, подвергнутых цементации или контурной закалке,

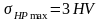д ля азотированных зубьев

7. Расчет зубчатых передач на изгибную прочность.

Проверочный расчет на прочность по напряжениям изгиба при перегрузках. Прочность зубьев, необходимую для предотвращения остаточных деформа­ций, хрупкого излома или образования первичных трещин в поверхностном слое, определяют из условия

т. е. сопоставляя расчетное и допусти­мое напряжения изгиба в опасном се­чении при максимальной нагрузке. Расчетное напряжение изгиба в опасном сечении

где F _1max— максимальная нагрузка; F₁—рабочая нагрузка/

Ориентировочно можно принимать σ_FPmax= 0,8σ_T при HB≤ 350 и σ_FPmax≈ 0,6 σ_T при НВ > 350 (здесь σ_T — предел текучести материала).

8. Материалы, применяемые при изготовлении зубчатых передач. Расчет допустимых напряжений.

Зубчатые колеса должны обла­дать необходимой износостойкостью рабочих поверхностей против выкра­шивания, абразивного изнашивания и заедания, а также требуемой прочнос­тью зубьев на изгиб.

Основные материалы для изготовле­ния зубчатых колес — термически обрабатываемые стали, в отдельных случаях чугуны и пластмассы. Материал и тех­нологию термообработки стали назна­чают в зависимости от условий работы передачи и размеров колес.

Для мало- и средненагруженных ре­дукторов общего назначения использу­ют качественные углеродистые стали 35, 40, 45, 50, 50Г (ГОСТ 1050-88*) и легированные стали 40Х, 45Х, 40ХН, 40ХНМ (ГОСТ 4543-71*) с твердостью НВ< 350. Такая твердость обеспечива­ется нормализацией или улучшением стали

В автотракторной отрасли промыш­ленности для изготовления зубчатых колес применяют низкоуглеродистые, высоколегированные цементуемые ста­ли с твердостью рабочей поверхности НВ>350, т.е. больше 35 HRC

9. Особенности расчета косозубых и шевронных цилиндрических передач

Геометрические параметры. У косозубых колес зубья рас­полагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол β (рис. 8.23, где а— косозубая передача; б — шевронная, и рис. 8.24). Оси колес при этом остаются параллельными. Для нарезания косых зубьев ИСПОЛЬЗУЮТ инструмент такого же исходного контура, как и для нарезания прямых. Поэтому профиль косого зуба в нормальном сечении п— п совпадает с профилем прямого зуба. Модуль в этом сечении должен быть также стандартным

В торцовом сечении t — t параметры косого зуба изменяются в зависимости от угла β

окружной шаг р_t =P_n/cosβ,

окружной модуль т_t = m_n/cosβ,

делительный диаметр d=m_tz = m_nz/cosβ.

Индексы п и t приписывают параметрам в нормальном и торцовом сечениях соответственно.

Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято опреде­лять через параметры эк­вивалентного прямозубого колеса .

В соответствии с этим форма косого зуба в нормальном сечении определяется эквивалентным прямозубым колесом, диаметр которого

d_v =d/cos²β

и число зубьев

z_v = d_v/m_n = d/(m_n cos² β) = m_t z/(m_t cos³β),

или

z_v = z/cos³β

Увеличение эквивалентных параметров (d_v иz_v) увеличением угла β является одной из причин повышения прочности косозубых передач. Вследствие наклона зубьев получается колесо как бы больших размеров или при той же нагрузке уменьшаются габариты передачи. Ниже показано, что косозубые передачи по сравнению с прямозубыми обладают еще и другими преимуществами: многопарность зацепления, уменьшение шума и пр. Поэтому в современных передачах косозубые колеса получили преимущественное распространение),

Расчет коэффициента торцового перекрытия

ε_α = [1,88 - 3,2 (1 /z₁ ±1 /z₂)] cosβ.

Силы в зацеплении. В косозубой передаче нормальную силу F_n раскладывают на три составляю­щие:

окружную силу F_t = 2T₁/ d₁,

осевую силу F_a = F_t tg β,

радиальную силу F_r = F'_t tg α_w=F_t tg α_w/cosβ,

в свою очередь, сила

F_n = F’_t/cos α_w = F_t/(cos α_w cos β).

Наличие в зацеплении осевых сил, которые дополнительно нагружают опоры валов, является недостатком косозубых колес. Этот недостаток устраняется в шевронной передаче, которая подобна сдвоенной косозубой передаче с противоположным направлением зубьев. Осевые силы здесь уравновешиваются на самом зубчатом колесе.

Расчет прочности зубьев по контактным напряжениям и расчет прочности зубьев по напряжениям изгиба выполняют по аналогии с прямозубыми передачами с учетом увеличения прочности косозубых передач.