Интегральная показательная функция

Интегральная показательная функция определяется следующим образом:

• expint(X) — возвращает интегральную показательную функцию для каждого элемента X, где Х может быть любым.

Пример:

» d=expint([2,3+7i]} 

d = 0.0489 -0.0013 -0.00601

Для вычисления этой функции используется ее разложение в ряд.

Ортогональные полиномы Лежандра

Функция Лежандра определяется следующим образом:

где Р_n(х) — полином Лежандра степени п, рассчитываемый как

• legendre(n.X) —возвращает функции Лежандра степени n и порядков m = 0,1..... n, вычисленные для элементов X. Аргумент n должен быть скалярным целым числом, не превосходящим 256, а X должен содержать действительные значения в области 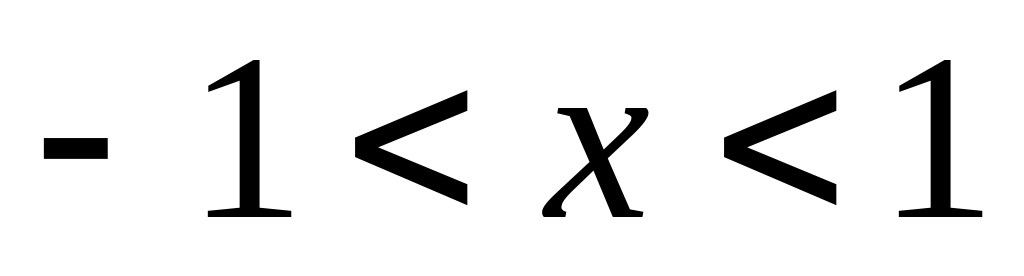- Возвращаемый массив Р имеет размерность n+1 lдля каждого аргумента Х.

• 1egendre(n,X, 'sch') — возвращает квазинормализованные по Шмидту функции Лежандра.

Пример:

>> g=rand(3,1);legendre(3,g)

ans =

0.7985 -0.2266 0.8300

-1.4401 1.2973 -1.3397

0.9985 2.3055 0.8437

-0.2718 -14.4445 -0.2093

Функции ошибки

Функция ошибки определяется следующим образом:

• erf(X) — возвращает значение функции ошибки для каждого элемента вещественного массива X.

Дополнительная (остаточная) функция ошибки задается соотношением:

• erfc(X) — возвращает значение остаточной функции ошибки.

• erfcx(X) — возвращает значение масштабированной остаточной функции ошибки. Эта функция определяется так:

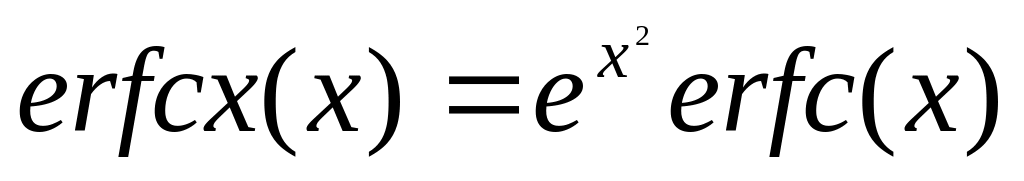
• erfinv(Y) — возвращает значение обратной функции ошибки для каждого элемента массива Y. Элементы массива Y должны лежать в области -1<Y<1.

Примеры: Определить все виды ошибок.

>> x=[2 -0.3 4 0.7];

>> erf(x)

ans = 0.9953 -0.3286 1.0000 0.6778

>> erfc(x)

ans = 0.0047 1.3286 0.0000 0.3222

>> erfcx(x)

ans = 0.2554 1.4537 0.1370 0.5259

>> erfinv(x)

ans = NaN -0.2725 NaN 0.7329

При вычислении данных функций используется аппроксимация по Чебышеву (см. детали алгоритма в Reference Book no MATLAB).

Эллиптические функции и интегралы

Эллиптические функции Якоби определяются интегралом и соотношениями

cn(u)=cosф,

dn(u) = (1-sin²ф)^1/2, 

аm(u) = ф.

В некоторых случаях при определении эллиптических функций используются модули k вместо параметра m. Они связаны выражением k = т = sin a .

• [SN, CN, DN] = ellipj(U, M) — возвращает эллиптические функции Якоби SN, CN и . DN, вычисленные для соответствующих элементов — аргумента U и параметра М. Входные величины U и М должны иметь один и тот же размер (или любая из них может быть скаляром).

• [SN, CN, DN] = ellipj(U, M, to1) — возвращает эллиптическую функцию Якоби, вычисленную с точностью tol . Значение tol по умолчанию — eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью.

Пример:

>> [SN,CN,DN]=ellipj([23.1],[0.5,0.2])

SN = 0.7222 0.1342

CN = 0.6916 -0.9909

DN = 0.8598 0.9982

Полные эллиптические интегралы первого и второго рода определяются следующим образом:

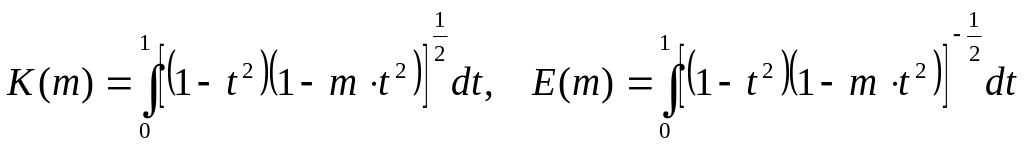
• ellipke(M) — возвращает полный эллиптический интеграл первого рода для элементов М.

• [К, Е] = ellipke(M) — возвращает полные эллиптические интегралы первого и второго рода.

• [К, Е] = ellipke(M, tol) — возвращает эллиптические функции Якоби, вычисленные с точностью tol. Значение по умолчанию — eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью.

Пример:

>> [f,e]=ellipke([0.2,0.8])

f = 1.6596 2.2572 e = 1.4890 1.1785

Для вычисления этих функций используется итерационный метод арифметико-геометрического среднего (см. детали в Reference Book по системе MATLAB).

7