Лекция № 23

Специальные математические функции.

1. Гамма-функция и ее варианты.

2. Бета-функция и ее варианты (эйлеров интеграл первого рода).

3. Функции Эйри.

4. Функции Бесселя.

5. Другие специальные функции.

Кроме элементарных функций, пакет MATLAB включает целый ряд специальных матема­тических функций, которые встречаются в задачах математической физики. Такие функции являются решениями некоторых дифференциальных уравнений или обозначениями инте­гралов определенного вида.

Технология вычисления специальных математических функций в системе Matlab практически не отличается от технологии вычисления элементарных функций. Пользователь вводит имя функции и значения аргументов. И после нажатия клавиши <Enter> получает значение специальной функции. Аргументами специальных математических функций могут быть как отдельные числа, так и массивы чисел. Если аргументом спецфункции является массив, в результате получится массив того же размера, элементы которого будут преобразованы в соответствии с заданной функцией.

Справку о функции можно получить, если ввести в командной строке doc function, где function — имя специальной функции.

Далее мы рассмотрим некоторые специальные математические функции, доступные в MATLAB.

Гамма-функция и ее варианты

Эта функция представлена несобственным интегралом на верхнем пределе и при на нижнем. Этот интеграл называется также эйлеровым интегралом второго рода.

Функция существует лишь при тех значениях параметра t , при которых сходится несобственный интеграл, т.е. при .

При натуральных значениях t (t = n) .

Гамма-функция в этом случае отождествляется с факториалом целого числа, при этом справедливыми являются следующие выражения: Гамма-функция существует для случая n целого, дробного, положительного и отрицательного, действительного и комплексного.

Гамма-функция в среде Matlab имеет представление только для действительного положительного n.

Неполная гамма-функция определяется как

• gamma (n) — возвращает гамма-функцию элементов n. Аргумент n должен быть вещественным.

• gammainс(X,n) — возвращает неполную гамма-функцию соответствующих элементов X и n. Аргументы X и n должны быть вещественными и иметь одинаковый размер (или любой из них может быть скалярным).

• gammaln(A) —возвращает логарифмическую гамма-функцию, gammaln(n) = 1og(gamma(A)). Команда gammaln позволяет избежать переполнения, которое может происходить, если вычислять логарифмическую гамма-функцию непосредственно, используя 1og(gamma(A)).

Примеры:

>> n=[0,1,2,6.5,-3,4.2];

>> d=gamma(n)

d = Inf 1.0000 1.0000 287.8853 Inf 7.7567

% из примера видно, что гамма-функцию чисел 0 и -3 программа не вычисляет

>> n=[0,1,2,6.5,3,4.2];

>> x=[2,4,5,6,5,3];f=gammainc(x,n)

f = 1.0000 0.9817 0.9596 0.4724 0.8753 0.3137

>> f=gammainc([4 5],[1 2])

f = 0.9817 0.9596

>> n=[0,1,2,6.5,-3,4.2];

>> k=gammaln(n)

k = Inf 0 0 5.6626 Inf 2.0486

Следует иметь в виду, что при вычислении факториала целого числа . Если необходимо вычислить 5!, то гамма-функция будет иметь вид: gamma(6)

>> gamma([1,2,3,-6,5.5, 6])

ans = 1.0000 1.0000 2.0000 Inf 52.3428 120.0000

Гамма-функция имеет довольно сложный».

>> ezplot(gamma(x),[-4,4])

>> grid on

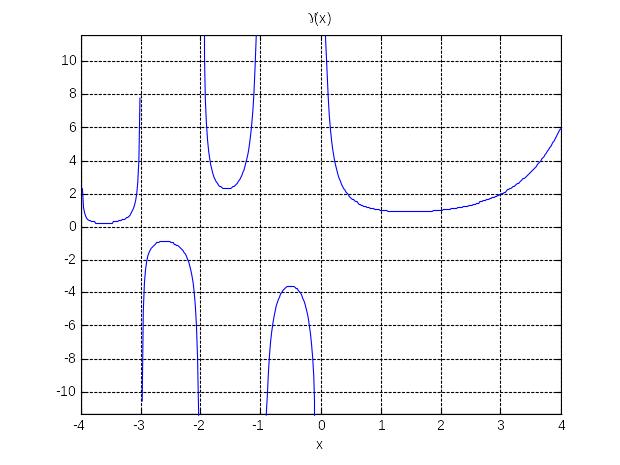
Рис. График гамма-функции

Это можно осуществить с помощью следующего файла-сценария:

%Ganrna- function graphicclear syms x

ezplot(gamma(x).[-4 4]) grid on

Гамма-функция вычисляется по известному алгоритму W. J. Kody (1989 г.). Для вычисления неполной гамма-функции используются рекуррентные формулы.