В. Применение круговой, диаграммы при измерении сопротивления нагрузки

Другой тип задач, решаемых с помощью круговой диаграммы, сводится к нахождению сопротивления нагрузки, находящейся на конце передающей линии. Если бы при этом были заданы длина линии и ее входное сопротивле­ние, то задача стала бы обратной предыдущей и решалась тривиаль­ным путем.

На практике, однако, приходится пользоваться другими исходными данными. Доступными для; измере­ний являются величина КСВ и фаза стоячей волны по отношению к на­грузке, определяемая по расстоянию минимума стоячей волны напряже­ния от нагрузки, как показано на рис. 1.10. Рассмотрим, каким обра­зом можно определить сопротивле­ние нагрузки, располагая этими дву­мя величинами.

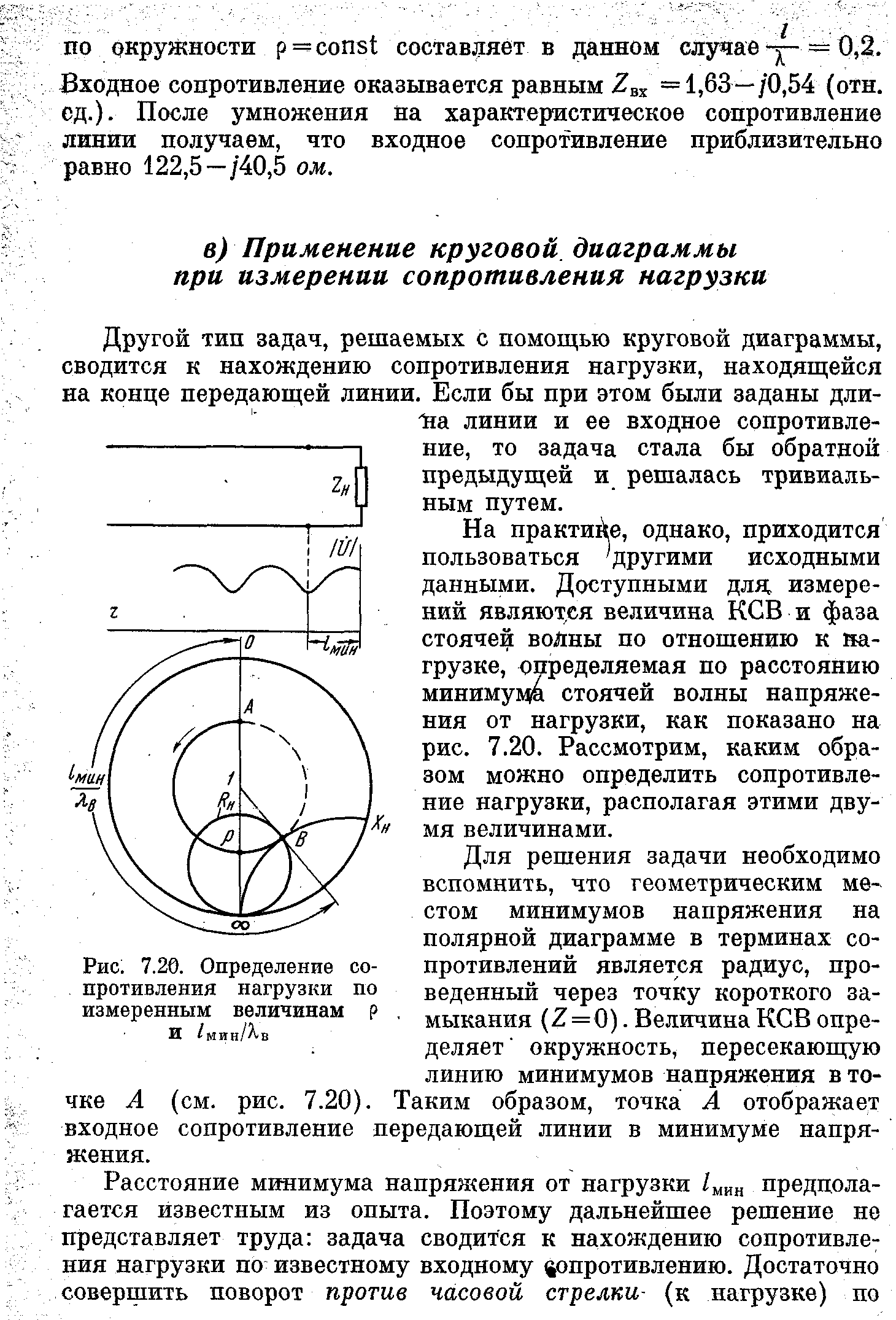
Рисунок 1.10. Определение со­противления нагрузки

по измеренным величинам  и .

Для решения задачи необходимо вспомнить, что геометрическим ме­стом минимумов напряжения на полярной диаграмме в терминах со­противлений является радиус, про­веденный через точку короткого за­мыкания (Z=0). Величина КСВ опре­деляет' окружность, пересекающую линию минимумов напряжения в то­чке А (см. рис. 1.10). Таким образом, точка А отображает входное сопротивление передающей линии в минимуме напря­жения.

Расстояние минимума напряжения от нагрузки l_мин предпола­гается известным из опыта. Поэтому дальнейшее решение не представляет труда: задача сводится к нахождению сопротивле­ния нагрузки по известному входному сопротивлению. Достаточно совершить поворот против часовой стрелки- (к нагрузке) по окружности = const и из точки А на угол , чтобы в точке В отсчитать сопротивление нагрузки.

Таким образом, измерение сопротивлений легко осуществля­ется путем измерения двух параметров, характеризующих стоя­чую волну в линии:  и . Этим объясняется столь широкое распространение измерений стоячих волн при помощи измерительных линий с подвижным зондом.

б)

a)

Рисунок 1.11. Опыт короткого замыкания нагрузки

для определения

а — стоячая волна напряжения при

закороченной нагрузке; б — стоячая волна при включе­нии рассматриваемой нагрузки

При работе с измерительными линиями не всегда бывает удобно непосредственно измерять расстояние от нагрузки до бли­жайшего минимума напряжения. Разумеется, можно воспользоваться отсчетом любого другого минимума стоячей волны, поскольку прибавле­ние целого числа полуволн не изме­няет результатов, получаемых с по­мощью круговой диаграммы. Однако и это измерение оказывается иногда неудобным и даже неосуществимым, например, при наличии переходов между измерительной линией и на­грузкой.

Указанное затруднение исключа­ется с помощью опыта короткого за­мыкания нагрузки, поясняемого на рисунке 1.11. При коротком замыкании нагрузки фиксируется положение одного из минимумов напряжения, находящегося в пределах рабочего участка измерительной линии. От­счет здесь может производиться по отношению к любому произвольно выбранному началу координат. За­тем нагрузка подключается к линии и изме-ряются величина КСВ и поло­жение минимума напряже-ния, бли­жайшего к ранее найденному со сто­роны гене-ратора. Расстояние между двумя найденными положе-ниями минимумов в точности равно расстоянию l_мин от нагрузки до ближайшего минимума напряжения, необходимому для расче­та. Дальнейшие манипуляции по определению сопротивления на­грузки не отличаются от описанных.

Рассмотренная методика применима к измерению полных со­противлений, в любых однородных передающих линиях. При определении угла поворота по диаграмме в общем случае следует учитывать длину волны в линии т. е. искать отношение .

Величина определяется непосредственно из описанного опы­та короткого замыкания нагрузки, как удвоенное расстояние между двумя соседними минимумами стоячей волны. Измерение сопротивления нагрузки в случае волноводных линий заканчи­вается определением его величины в относительных единицах.

Выбор плоскости короткого замыкания (так называемой плоскости эквивалентного представления нагрузки) часто опреде­ляется непосредственно геометрией исследуемой нагрузки. В слу­чае полых резонаторов этот вопрос решается путем сильной рас­стройки резонатора относительно резонансной частоты.

Методика измерения полных проводимостей с помощью изме­рительной линии и круговой диаграммы полностью повторяет описанную выше процедуру. Небольшое отличие заключается лишь в выборе на диаграмме исходной точки, соответствующей минимуму стоячей волны напряжения. Поворот по окружности  = const, производимый здесь, как обычно, против часовой стрел­ки, должен начинаться из точки пересечения окружности посто­янного КСВ с линией чисто активных проводимостей на участке ч между центром диаграммы и точкой бесконечно большой прово­димости. Некоторые дополнительные соображения по этому вопросу приводятся в нижеследующем разделе.