СОДЕРЖАНИЕ

ВВЕДЕНИЕ………………………………………………………….. 4

1. КРУГОВАЯ ДИАГРАММА ПОЛНЫХ СОПРОТИВЛЕНИЙ И ПРОВОДИМОСТЕЙ ПЕРЕДАЮЩИХ ЛИНИЙ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ ………………………………..…5

2. ОСНОВНЫЕ ПРИМЕНЕНИЯ КРУГОВЫХ ДИАГРАММ …..21

3. Примеры решения задач …………………………...……39

4. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ………72

5. КОНТРОЛЬНЫЕ ВОПРОСЫ …………………………………...82

6. СПИСОК ЛИТЕРАТУРЫ ……………………………………….85

ВВЕДЕНИЕ

Одним из составных элементов сверхвысокочастотных систем приема и передачи информации являются передающие линии, для расчета которых с успехом применяется теория длинных линий. В пределах этого раздела студенты должны изучить основные понятия, относящиеся к волноведущим структурам (передающим линиям). Эти понятия являются достаточно общими и применимы к системам телефонной связи, кабельного телевидения, сетей ЭВМ и т.д. Студенты должны уметь применить эти знания для решения задач по следующим темам:

• первичные и вторичные параметры длинных линий,

• расчет параметров различных типов линий,

• процессы в линиях с потерями,

• входное сопротивление отрезка длинной линии,

• диаграмма Вольперта-Смита,

• согласование нагрузок.

При изучении курса «Техника и электроника СВЧ» студентам необхо­димо обратить внимание на взаимосвязь математического формализма и физического содержания рассматриваемых процессов., Особенно должен помочь энергетический подход к рассмотрению изучаемых систем. Помните, что усвоенные понятия будут развиваться и приме­няться в течение всего срока учебы, а затем и в практической деятель­ности.

При рассмотрении приведенных примеров решения задач, и са­мостоятельном решении задач необходимо прежде всего уяснить суть физических процессов, происходящих в рассматриваемой системе, и тогда поставленная цель будет достигнута.

1. Круговая диаграмма полных сопротивлений

И ПРОВОДИМОСТЕЙ ПЕРЕДАЮЩИХ ЛИНИЙ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ

При расчетах передающих линий СВЧ часто приходится определять входное сопротивление линий, нагруженной на известное сопротивление, либо производить другие сходные вычисления В принципе для таких вычислений можно использовать уравнение

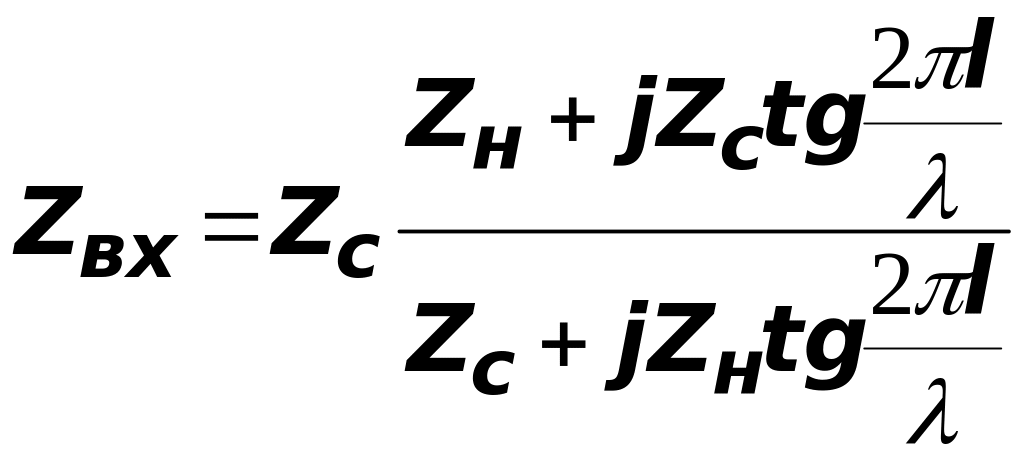, (1.1)

где - характеристическое (волновое) сопротивление линии;

- комплексное сопротивление нагрузки;

l – длина рассматриваемого отрезка линии;

- рабочая длина волны.

При коротком замыкании на конце шлейфа =0 и входное сопротивление

. (1.2)

Расчеты могут быть чрезвычайно упрощены, если восполъзоваться специальным типом круговых диаграмм (номограмм). Одним из первых подобные диаграммы предложил советский ин­женер А. Р. Вольперт. Создание круговых диаграмм для пере­дающих линий СВЧ связывают также с именем Смита.

Для обоснования принципов построения круговой диаграммы рассмотрим уже обсуждавшуюся векторную диаграмму токов и напряжений в передающей линии без потерь. Диаграмма воспро­изведена с дополнительными пояснениями на рисунке 1.1.

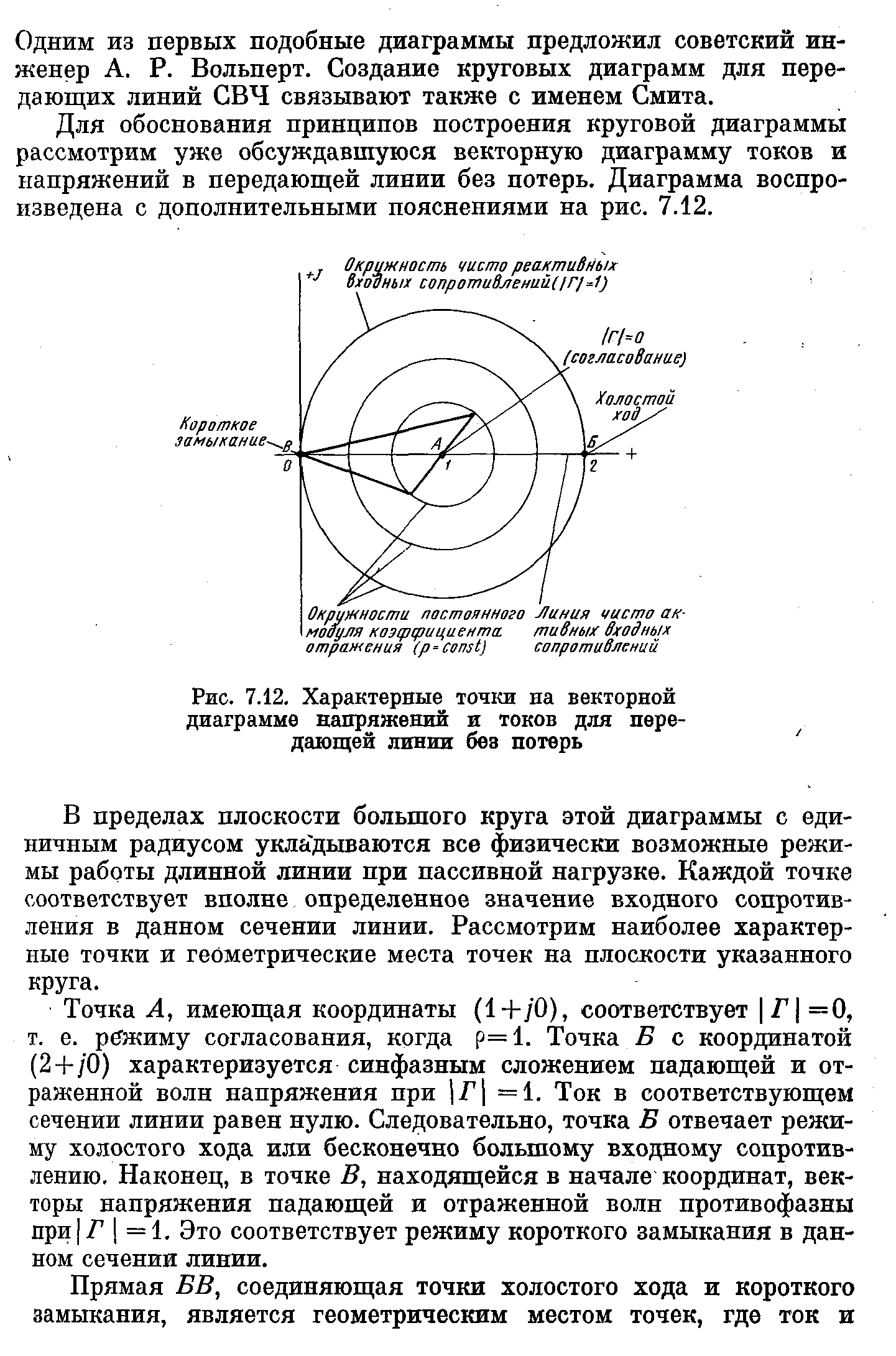
Рисунок 1.1 Характерные точки на векторной диаграмме напряжений и токов для пере­дающей линии без потерь

В пределах плоскости большого круга этой диаграммы с еди­ничным радиусом укладываются все физически возможные режи­мы работы длинной линии при пассивной нагрузке. Каждой точке соответствует вполне определенное значение входного сопротив­ления в данном сечении линии. Рассмотрим наиболее характер­ные точки и геометрические места точек на плоскости указанного круга.

Точка А, имеющая координаты (1+j0), соответству-ет |Г| =0, т. е. режиму согласования, когда  = 1. Точка Б с координатой (2+j0) характеризуется синфазным сложением падающей и от­раженной волн напряжения при |Г| = 1. Ток в соответствующем сечении линии равен нулю. Следовательно, точка Б отвечает режи­му холостого хода или бесконечно большому входному сопротив­лению. Наконец, в точке В, находящейся в начале координат, век­торы напряжения падающей и отраженной волн противофазны при |Г|=1. Это соответствует режиму короткого замыкания в дан­ном сечении линии.

Прямая БВ, соединяющая точки холостого хода и короткого замыкания, является геометрическим местом точек, где ток и напряжение синфазны. Следовательно, прямая БВ является геометрическим местом чисто активных входных сопротивлений, изме­няющихся от нуля (точка В) до бесконечности (точка Б).

Согласно доказанным свойствам стоячих волн, на отрезке АБ располагаются входные сопротивления в минимумах стоячей вол­ны напряжения, а на отрезке АБ – входные сопротивления в мак­симумах стоячей волны. Величина сопротивлений в максимумах и минимумах стоячей волны напряжения находится из следую­щих выражений:

Учитывая, что

получим:

(1.3)

(1.4)

Б

(1.3)

(1.4)

ольшая окружность единичного радиуса с центром в точке А на рисунке 1.1 соответствует случаю |Г |=1. Теоретически по уравнению

(1.5)

равенство единице модуля коэффициента отра­жения возможно либо при коротком замыкании, либо при холос­том ходе линии, или при чисто реактивной нагрузке. Поскольку точки холостого хода и короткого замыкания найдены, заключаем, что рассматриваемая окружность является геометрическим местом чисто реактивных входных сопротивлений линии. Верхняя полу­плоскость на рисунке 1.1 соответствует положительным, т. е. индук­тивным сопротивлениям, нижняя – отрицательным (емкостным) сопротивлениям. Для подтверждения этого достаточно вспомнить выражение (1.2) для входного сопротивления короткозамкнугой линии.

Окружности с центром в точке А являются линиями постоян­ного модуля коэффициента отражения |Г| или, что то же, линия­ми постоянного КСВ. Величина радиуса численно равна |Г|. Пере­мещению вдоль оси передающей линии на равные отрезки соот­ветствует перемещение на диаграмме по окружности постоянного КСВ на равные углы. Полный оборот по диаграмме совершается при перемещении вдоль линии на или, в случае линии без дисперсии, на .

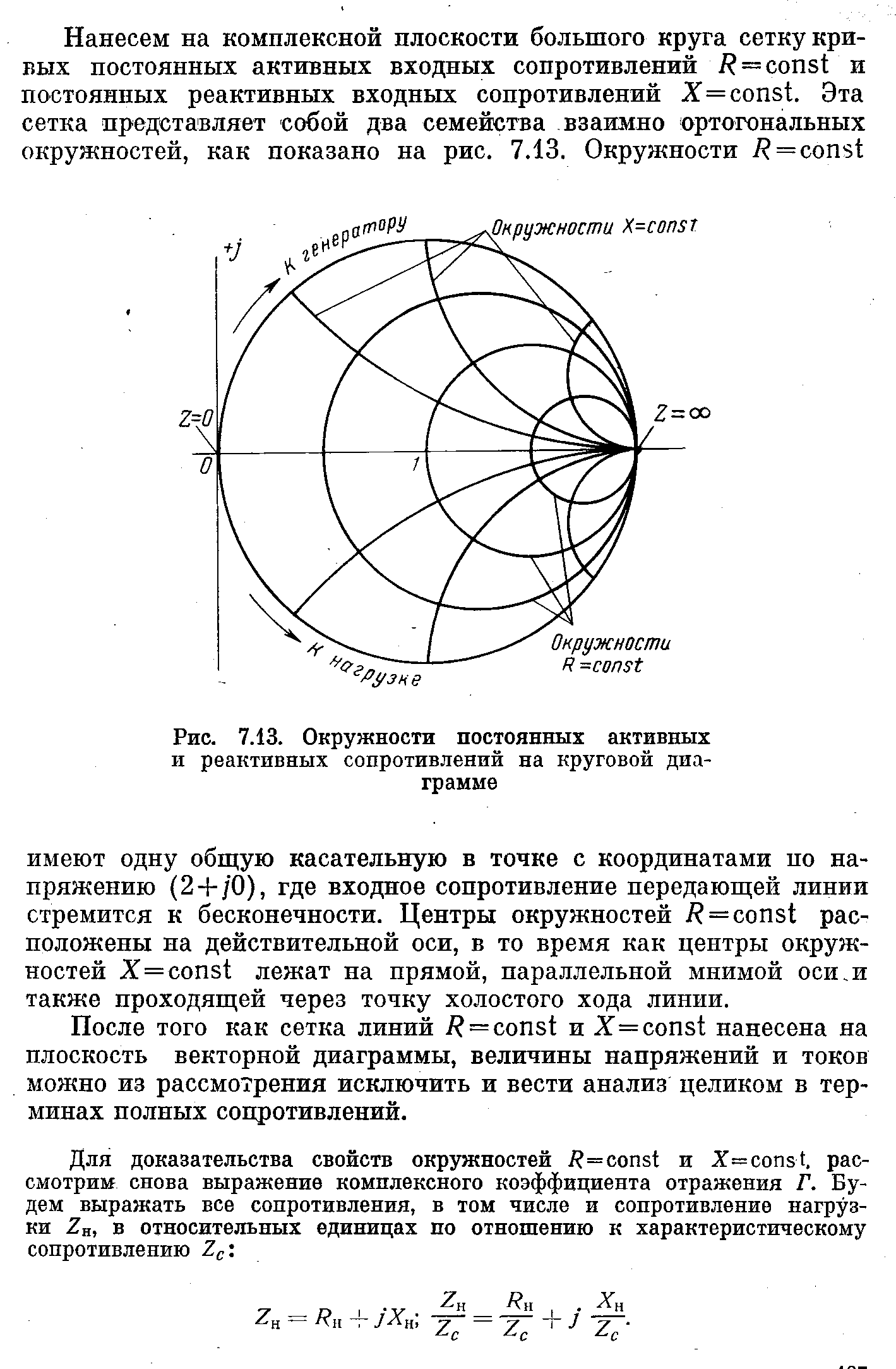
Нанесем на комплексной плоскости большого круга сетку кри­вых постоянных активных входных сопротивлений R= const и постоянных реактивных входных сопротивлений Х=const. Эта сетка представляет собой два семейства взаимно ортогональных окружностей, как показано на рисунке 1.2. Окружности R=const имеют одну общую касательную в точке с координатами по на­пряжению (2+j0), где входное сопротивление передающей линии стремится к бесконечности. Центры окружностей R= const рас­положены на действительной оси, в то время как центры окруж­ностей Х=const лежат на прямой, параллельной мнимой оси и также проходящей через точку холостого хода линии.

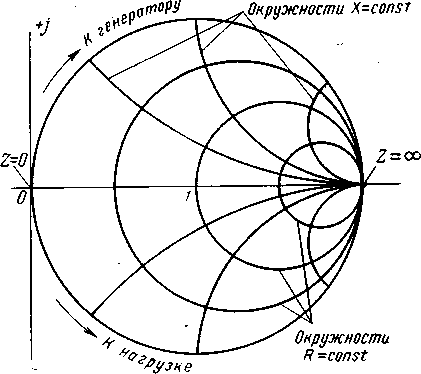
Рисунок 1.2. Окружности постоянных активных и реактивных сопротивлений на круговой диа­грамме

После того как сетка линий R= const и Х=const нанесена на плоскость векторной диаграммы, величины напряжений и токов можно из рассмотрения исключить и вести анализ целиком в тер­минах полных сопротивлений.

Для доказательства свойств окружностей R=const и X=const рас­смотрим снова выражение комплексного коэффициента отражения Г. Бу­дем выражать все сопротивления, в том числе и сопротивление нагруз­ки Z_H, в относительных единицах по отношению к характеристическому сопротивлению Z_C:

(1.6)

(1.3)

Характеристическое сопротивление передающей линии в относитель­ных единицах Z_c = l. Сопротивление нагрузки в относительных единицах будем здесь для простоты записывать без индексов:

Z = R+jX (отн. ед.). (1.7)

Тогда из выражения (1.5) коэффициент отражения

(1.8)

П

(1.9)

редставим коэффициент отражения в комплексной форме:

(1.9)

и найдем величины Г' и Г" из уравнений (1.7) и (1.8). Очевидные пре­образования дают:

(1.10)

(1.10)

Исключим из этих выражений сначала R, а потом X. После несколь­ких искусственных преобразований можно получить:

(1.11)

(1.12)

(1.11)

(1.12)

Найденные выражения являются уравнениями окружностей на ком­плексной плоскости Г=Г'+jГ". Параметром в первом уравнении является активное сопротивление R, во втором — реактивное сопротивление X. Этим доказано, что линии постоянных R и X являются окружностями.

Координаты центров окружностей R=const согласно выражению (1.11) равны:

(1.13)

(1.13)

Р

(1.14)

адиус окружностей R=const оказывается равным

(1.14)

Окружности Х=const согласно соотношению (7.28) имеют координаты центров

(1.15)

(1.15)

и радиус .

Пользуясь этими уравнениями, можно рассчитать и построить сетку окружностей R=const и X=const, показанных на рисунке 1.3.

Сетку окружностей  = const на круговой диаграмме либо во­все не проводят, либо наносят в виде пунктира. В соответствии с соотношениями (7.23) и (7.24) окружности =const пересекают действительную ось в точках, через которые проходят окружно­сти R=const, причем в относительных единицах R= или R=1/.

Таким образом, для нахождения окружности заданного КСВ не­обходимо найти соответствующую окружность R=const, после чего провести из центра диаграммы окружность, касательную к окруж­ности постоянного активного сопротивления. Последнее обстоя­тельство играет важную роль и упрощает практическую работу с круговой диаграммой.

За начало отсчета углов обычно принимают точку R = X=0, т. е. минимум стоячей волны напряжения. Шкалу углов наносят вне большой окружности. Углы выражают не в градусах, а в виде отношения длины линии

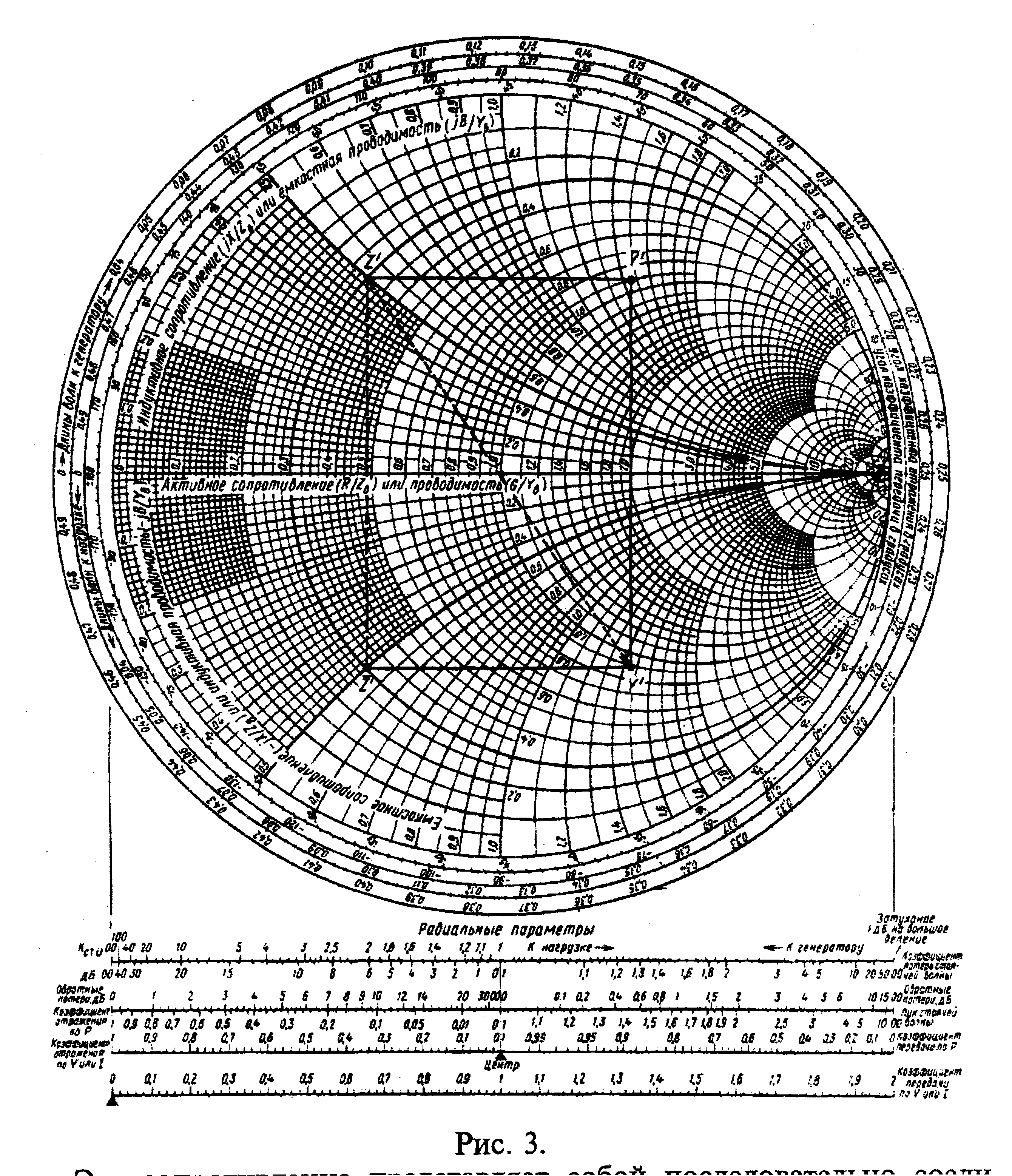
Рисунок 1.3. Окружности постоянных активных и реактивных сопротивлений на круговой диа­грамме Вольперта – Смита.

l к длине волны в данной линии _B, т. е. в единицах или, соответственно ,

Увеличению расстояния рассматриваемого сечения от нагруз­ки соответствует движение по окружности =const в направлении по часовой стрелке. Поэтому на диаграмме полных сопротивлений обычно делают надписи «к генератору» и «к нагрузке», соответ­ствующие отрицательному и положительному направлениям отсче­та углов. Во избежание ошибок при использовании этих надпи­сей следует всегда помнить физический смысл движения по окружности  = const, связывая его с исходной векторной диа­граммой токов и напряжений в передающей линии.

Поскольку токи и напряжения из непосредственного рассмот­рения выпадают, оси прямоугольных координат, показанные на рисунках 1.2 и 1.3, опускают. Отсчет производят в полярной системе координат и . В связи с этим рассмотренная диаграмма полных сопротивлений носит название круговой диаграммы в полярной системе координат.

В окончательном виде полярная диаграмма полных сопротив­лений передающих линий показана на рисун-ке 1.4. Эта диаграмма является универсальной и пригод­на для расчетов любых передающих линий в пределах применимо­сти понятия характеристического сопротивления, если линия воз­буждена на волне одного типа. Для удобства работы с диаграммой последняя иногда снабжается прозрачным движком, вращающим­ся относительно центра диаграммы.

К

(1.16)

оординатная сетка диаграммы, показанная на рисунке 1.4, мо­жет быть применена для изображения не только полных сопротив­лений линии, но и полных проводимостей в относительных еди­ницах:

(1.16)

где

(1.17)

(1.18)

(1.17)

(1.18)

Доказательство применимости диаграммы в терминах полных проводимостей может быть проведено с помощью теории функций комплексного переменного, поскольку преобразование типа (1.16) относится к числу конформных.

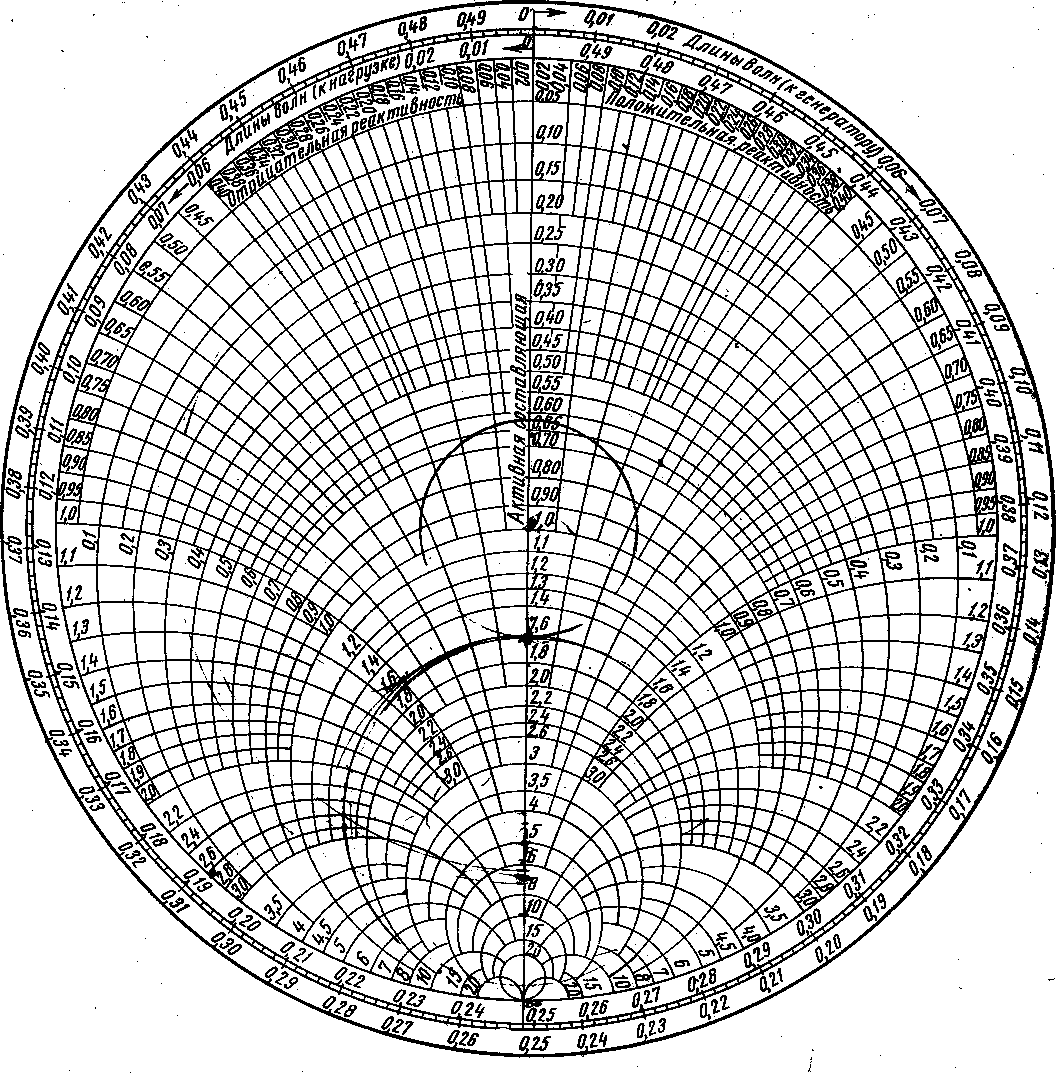
Рисунок 1.4. Круговая диаграмма полных сопротивлений

и проводимостей в полярной системе координат

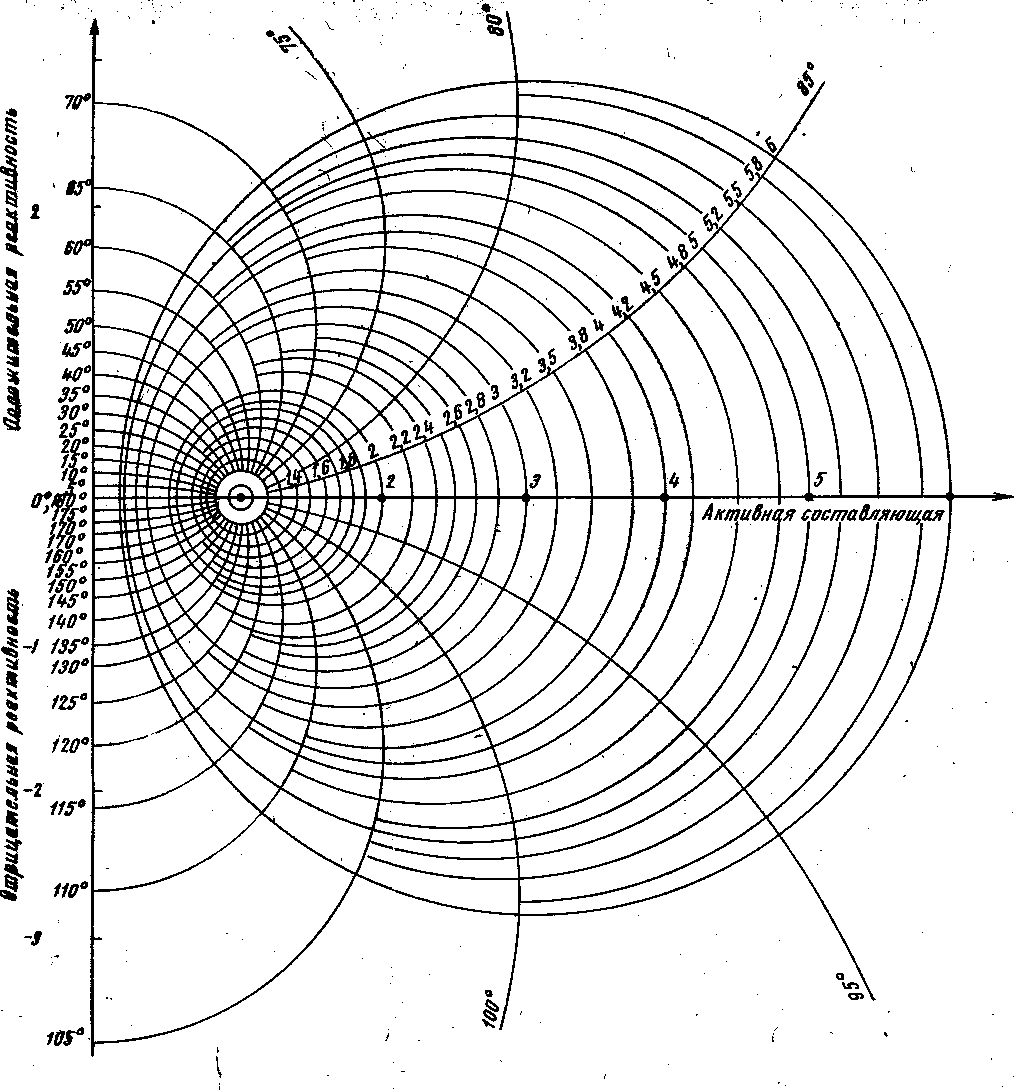
Рисунок 1.5. Круговая диаграмма полных сопротивлений и проводимостей в прямоугольной системе координат.

При пользовании полярной диаграммой в терминах проводи­мостей остаются в силе все без исключения числовые обозначения, имеющиеся на диаграмме сопротивлений. Меняется только физи­ческий смысл характерных точек. Точка Б на рисунке 1.2 означает теперь не режим холостого хода, а режим короткого замыкания. Наоборот, точка В соответствует теперь холостому ходу (Y=0). Минимумам стоячей волны напряжения соответствует отрезок АБ. Верхняя полуплоскость на рисунке 1.2 соответствует по-прежне­му положительной реактивности, но уже не индуктивности, а емкости и т. д.

Помимо круговой диаграммы в полярной системе координат, суще­ствуют другие типы диаграмм полных сопротивлений и проводимостей передающих линий. Чаще других из их числа применяется диаграмма в прямоугольной системе коорди­нат, являющаяся отображением по­лярной диаграммы на комплексную плоскость R+jX или G+jB.

Рисунок 1.6. Окружности постоян­ных значений КСВ и постоянной фазы на плоскости полных со­противлений в прямоугольной системе координат

Принцип построения этой диа­граммы в терминах сопротивлений показан на рисунке 1.6. Координаты активных и реактивных сопротив­лений R и X отложены соответст­венно по осям абсцисс и ординат. Линии постоянных значений КСВ и постоянной фазы представ­ляют собой два взаимно ортого­нальных семейства окружностей.

Радиус R₀ окружностей постоян­ного КСВ определяется в относи­тельных единицах из полученных ранее условий (1.7) и (1.8):

(1.19)

(1.19)

Центры окружностей q = const лежат на действительной оси в точ­ках с координатой R₁, равной

(1.20)

(1.20)

Центры окружностей постоянной фазы лежат на мнимой оси в точках с координатой

(1.21)

(1.21)

где l – расстояние от нагрузки до рассматриваемого сечения линии. Радиус Х₀ окружностей = const оказывается равным

(1.22)

(1.22)

Линии R=const и X=const на диаграмме в прямоугольной системе координат имеют вид параллельных горизонтальных и вертикальных прямых. Сетка прямых постоянных активных и реактивных сопротивлений на плоскость диаграммы для простоты не наносится.

Диаграмма полных сопротивлений в прямоугольной системе коорди­нат, построенная по указанным выше соотношениям, приведена на рисунке 1.5. Подобно диаграмме в полярных координатах, эта круговая диаграмма может с одинаковым успехом применяться в тер­минах полных проводимостей. По оси абсцисс в таком случае должна от­кладываться активная проводимость G,апо оси ординат — реактивная проводимость jB в относительных единицах (по отношению к характеристиче­ской проводимости линии, принимаемой за единицу).