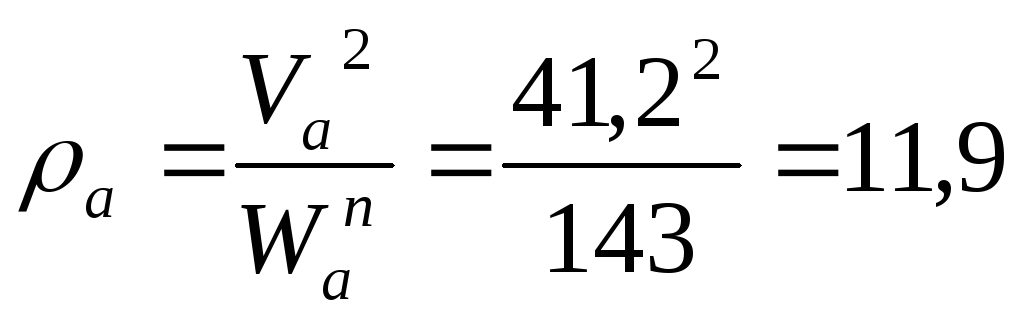УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ

Задание 2К

Составное движение точки

Вариант 24

Выполнил: Хусаинов Т.М.

Проверил: Ильчанинов В.П

г. Уфа

2007год

Трубка вращается вокруг неподвижной оси с угловой скоростью и наклонена к этой оси под углом . В трубке движется шарик М по закону OM = S(t)

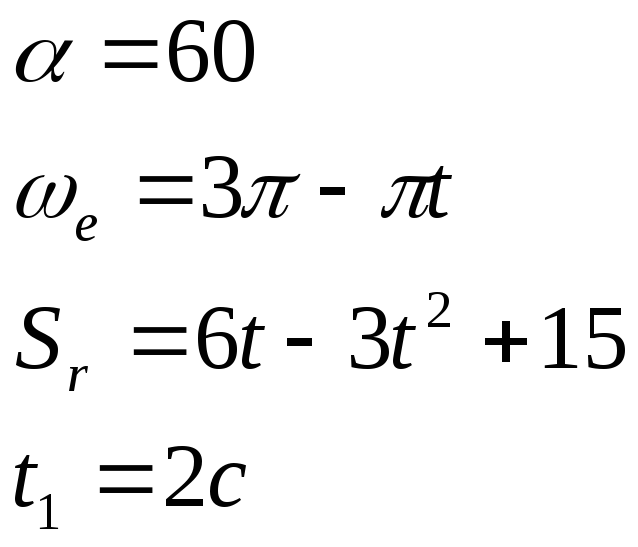
Решение:

Найдем расстояние точки M от центра O в момент времени

Далее определим вектор относительной скорости:

и вектор переносной скорости:

где - условный радиус кривизны траектории, так же он называется радиусом переносного вращения.

и - угловая скорость в момент времени

Вектор абсолютной скорости находится по формуле:

Так как следовательно найти вектор абсолютной скорости можно по формуле

Так же модуль вектора абсолютной скорости можно найти по проекциям вектора абсолютной скорости на оси координат

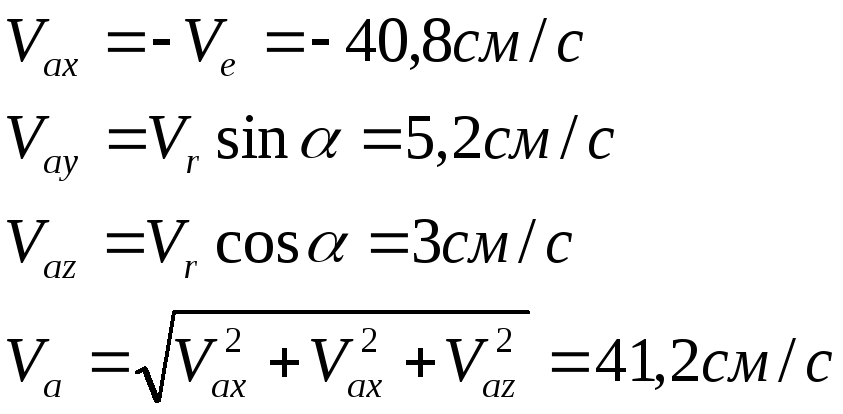
Определим вектора ускорений

- формула величины переносного ускорения при переносном вращательном движении

- величина относительного ускорения

здесь , т.к. совершается относительное движение по прямой

- ускорение Кориолиса

далее найдем модули всех составляющих векторов ускорений:

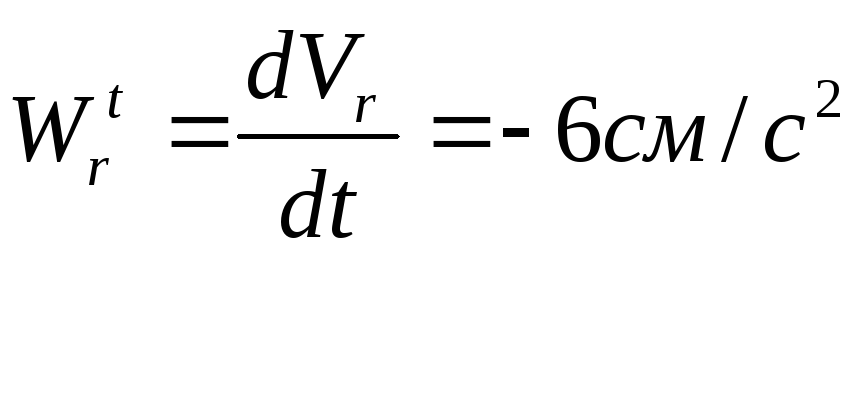- нормальная составляющая относительного ускорения точки

- угловое ускорение переносящего тела

тангенциальная, нормальная, и кариолисова составляющие находятся по формулам:

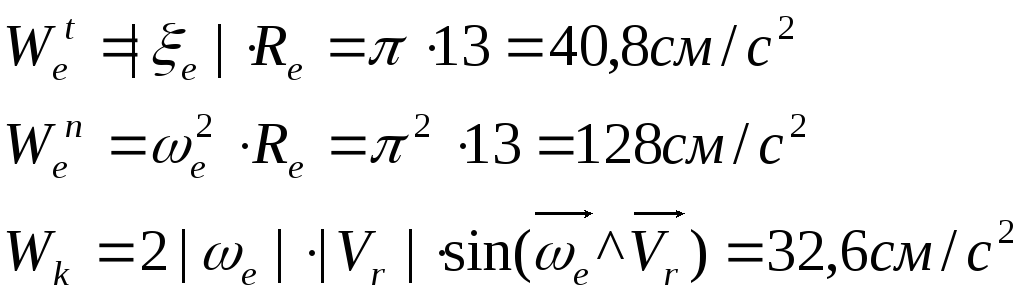
Определим модуль вектора абсолютного ускорения точки М по формуле

найдем проекции абсолютного ускорения на координатные оси:

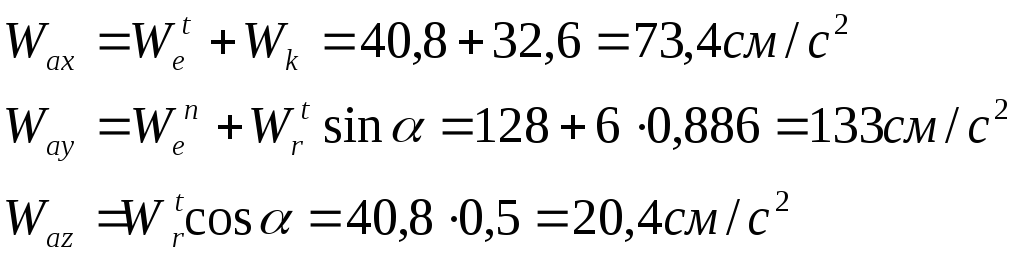
Теперь определим величины нормальной и касательной составляющих вектора абсолютного ускорения точки М по формуле

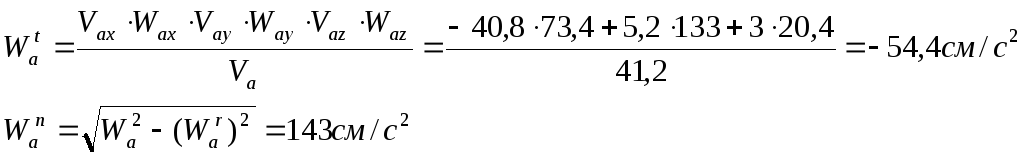
Вычислим радиус кривизны абсолютной траектории точки М в заданный момент времени