Лекція 1 основні поняття математичної фізики. диференціальні рівняння з частинними похідними

1.1 Предмет математичної фізики. Диференціальні рівняння з частинними похідними

Предметом математичної фізики, як відомо [3], є вивчення методів розв’язування задач, що виникають при аналізі широкого класу фізичних явищ, які моделюються диференціальними рівняннями з частинними похідними. Ці рівняння називаються рівняннями математичної фізики. Ми не ставимо перед собою задачу вивчати всі способи розв’язування диференціальних рівнянь з частинними похідними. Розглянемо тільки ті конкретні рівняння, які є дуже важливими для фізики, механіки і техніки.

Зупинимось на основних поняттях таких рівнянь.

Диференціальним рівнянням з частинними похідними відносно невідомої функції називається рівняння, що зв’язує незалежні змінні , шукану функцію та її частинні похідні. Найвищий порядок частинної похідної, що входить в рівняння, називається порядком диференціального рівняння.

Наприклад, – є диференціальним рівнянням з частинними похідними 2-го порядку для функції класу .

Функція називається розв’язком диференціального рівняння з частинними похідними, якщо в результаті підстановки її в рівняння воно перетворюється в тотожність.

Приклад 1.1 Знайти функцію , яка є розв’язком диференціального рівняння .

Домножимо обидві частини рівняння на і зінтегруємо по змінній :

,

де – довільна функція від (ця функція відіграє роль довільної сталої при інтегруванні по ).

Знову домножимо обидві частини рівняння на та проінтегруємо по :

У результаті отримаємо

,

де – друга довільна функція від .

Перевіркою легко встановити, що знайдена функція задовольняє задане рівняння, отже, є його розв’язком.

Як бачимо, функція залежить від двох довільних двічі диференційовних функцій та У цьому і полягає відмінність розв’язування диференціальних рівнянь з частинними похідними у порівнянні з розв’язуванням диференціальних рівнянь зі звичайними похідними, де розв’язок залежить від довільних сталих. Знайдена функція є загальним розв’язком даного диференціального рівняння з частинними похідними.

Диференціальне рівняння з частинними похідними називається лінійним, якщо шукана функція і всі її частинні похідні входять в рівняння лінійно. Рівняння з частинними похідними називається квазілінійним, якщо воно лінійне відносно всіх старших похідних від невідомої функції.

Диференціальні рівняння математичної фізики, якими ми будемо займатись в подальшому, мають між собою чимало спільного [1]: усі вони – другого порядку, лінійні відносно невідомої функції та її частинних похідних, а коефіцієнти перед функцією та її похідними – сталі числа. Загальний вигляд таких рівнянь для функції є наступним:

,

де – сталі, а права частина – задана функція від .

1.2 Зведення до канонічного виду диференціального рівняння другого порядку

Розглянемо диференціальне рівняння з частинними похідними, яке є лінійним відносно похідних другого поряд-ку:

(1.1)

де A, B, C – сталі (в загальному випадку можуть бути і функціями, визначеними в деякій області D площини xOy з неперервними похідними до другого порядку включно), F – неперервна функція [4].

Л. Ейлер довів, що будь-яке диференціальне рівняння виду (1.1) за допомогою заміни незалежних змінних і можна привести до одного з трьох видів (типів), відомих як гіперболічний, параболічний та еліптичний (по аналогії з теорією кривих другого порядку в курсі аналітичної геометрії) [1].

Поставимо задачу: за допомогою заміни змінних x і y звести рівняння (1.1) до найпростішого (канонічного) виду. Введемо нові змінні

(1.2)

Нехай функції і – двічі неперервно-диференційовані і якобіан

в області D.

Виразимо похідні через нові змінні:

, ;

Підставляючи ці похідні в (1.1), отримаємо:

(1.3)

де

Явний вираз нас не цікавить. Спробуємо вибрати функції і так, щоб деякі із коефіцієнтів , , стали рівними нулю. Очевидно, щоб вирішити питання про рівність нулю коефіцієнтів та , достатньо розв'язати еквівалентне завдання про розв'язок наступного диференціального рівняння першого порядку відносно деякої функції z(x, y), яку будемо називати характеристичною функцією:

(1.4)

Поділивши (1.4) на отримаємо квадратне рівняння відносно

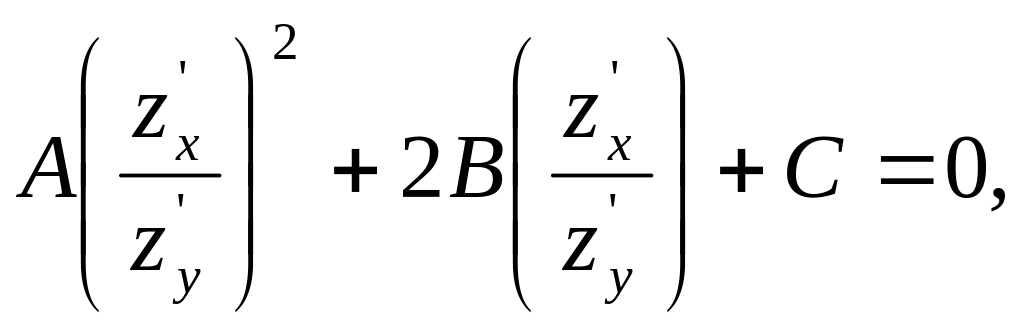яке фактично розпадається на два:

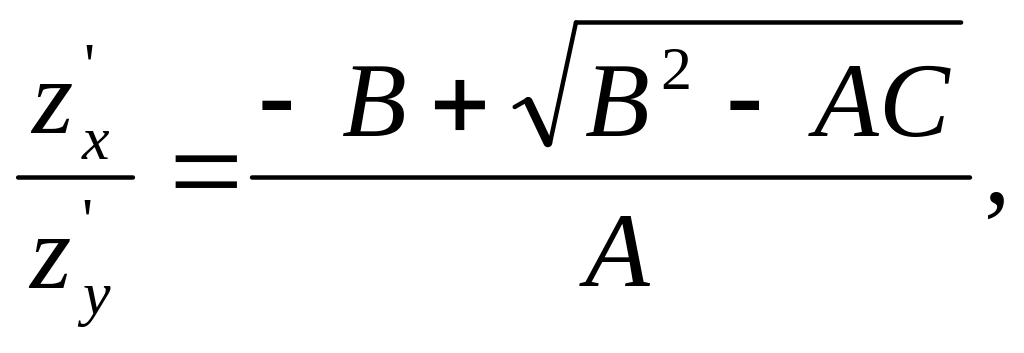(1.5) (1.6)

Криву z(x, y)=const, що є розв’язком рівняння (1.4) будемо називати характеристичною кривою, а саме рівняння (1.4) − рівнянням характеристик.

З умови z(x, y)= const випливає, що

z'_x dx+ z'_y dy = 0.

Звідси маємо простий зв'язок з похідними функції z(x, y)

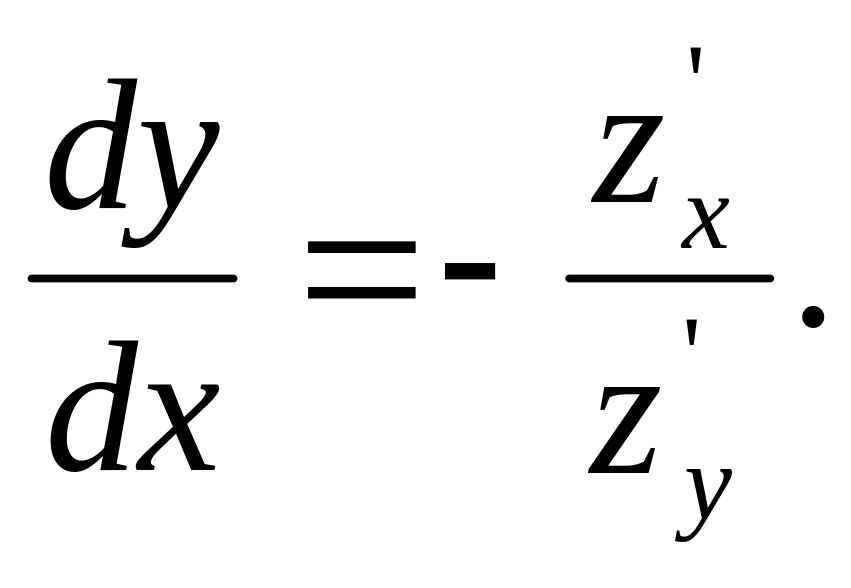
Ввівши відповідну заміну в (1.5) і (1.6), отримаємо :

(1.7) (1.8)

Розв'язки рівнянь (1.5) і (1.6) пов'язані з розв'язком рівнянь (1.7) і (1.8) наступним чином. Нехай

, (1.9)

− загальні інтеграли рівнянь (1.7) і (1.8).

Тоді функції і будуть розв'язками рівнянь (1.5) і (1.6) відповідно, а значить і розв'язками рівняння (1.4). Криві (1.9) називаються характеристиками рівняння (1.1). Зазначимо, що рівняння (1.7) і (1.8) у загальнішій формі можна подати у вигляді одного характеристичного рівняння:

А(dy)²−2Bdxdy+C(dx)²=0. (1.10)

Очевидно, що розв’язки рівнянь (1.7) і (1.8), а значить канонічний вид рівняння (1.1), залежить від знаку дискримінанта D=В²−АС, або знаку визначника

у всій області .

У залежності від цього розглянемо три випадки:

1) Нехай у розглядуваній області ∆ < 0 (D = В²−АС >0) − рівняння гіперболічного типу (можна вважати, що або , або ).

У цьому випадку загальні інтеграли (1.9) визначають дві дійсних і різних сім'ї характеристик. Оскільки функції φ(x, y) і ψ(x, y) задовольняють рівняння (1.4), то, поклавши в (1.2)

, , (1.11)

отримаємо (оскільки знак дискримінанта не змінюється при заміні змінних).

Розділивши рівняння (1.3) почленно на 2В, одержимо канонічний вид рівняння гіперболічного типу:

.

При рівняння (1.1) належить гіперболічному типу і вже має канонічний вид. Якщо рівняння (1.1) було лінійним відносно похідних першого порядку і самої функції , то після перетворення рівняння також буде лінійним. Якщо в цьому рівнянні покласти , , то рівняння набуде вигляду:

.

Це другий канонічний вид рівняння канонічного типу.

2) Нехай ∆=0 (D=В²−АС=0) – рівняння параболічного типу. В силу вказаної умови можна припустити, що в кожній точці розглядуваної області один з коефіцієнтів , відмінний від нуля. Нехай .

У цьому випадку загальні інтеграли (1.9) дійсні і співпадають. Таким чином, є тільки одна сім'я характеристик. Рівняння (1.5) і (1.6) також співпадають і набувають вигляду

Не важко бачити, що будь-який розв’язок цього рівняння в силу задовольняє також рівняння:

Врахувавши це, маємо ξ= φ(x, y), а за η(x, y), візьмемо будь-яку двічі неперервнодиференційовну функцію, для якої якобіан

Тоді . Враховуючи, що D = 0 ( а це означає що і ), отримаємо, що , а коефіцієнт набуває виду

Поділивши рівняння (1.3) на одержимо канонічне рівняння параболічного типу:

.

Зауважимо, якщо , а , то отримали б аналогічне канонічне рівняння з зліва.

3) Нехай ∆>0 (D=В²−АС <0) − рівняння еліптичного типу.

Тут загальні інтеграли (1.9) є комплексними величинами. Тобто рівняння еліптичного типу не мають дійних характеристик. Нехай φ(x, y)≡ φ₁(x, y)+ іφ₂(x, y)= С₁ − один із загальних інтегралів (1.9); другий загальний інтеграл буде комплексно спряженим з даним.

Покладемо в (1.2):

ξ= φ₁(x, y) , η=φ₂(x, y).

Підставляючи в рівняння (1.4) його розв'язок φ=ξ+іη, отримаємо

Відокремлюючи у цій тотожності дійсну та уявну частини, одержимо:

Звідси випливає, що . Очевидно, що . Тоді отримаємо рівняння еліптичного виду:

Приклад 1.2 Знайти загальний розв’язок рівняння, звівши його до канонічного виду

.

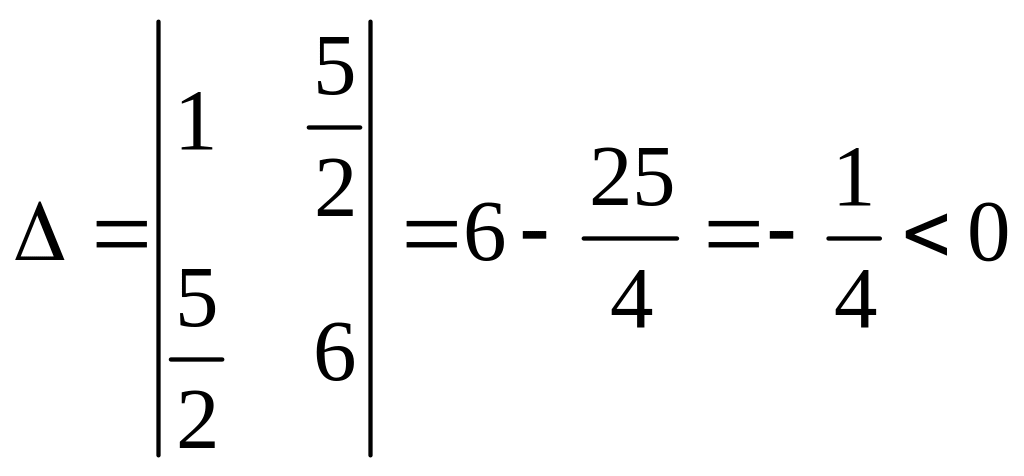Тут . Отже, задане рівняння гіперболічного типу.

Запишемо рівняння характеристик .

Поділивши на , отримаємо .

Знайдемо .

Розв’яжемо ці рівняння.

,

.

Введемо заміну змінних

або

Знайдемо всі частинні похідні, що входять у задане рівняння, виразивши їх через :

Підставивши у задане рівняння, отримаємо

.

Після спрощень одержуємо .

Інтегруємо по змінній (можна по ). Тоді , де – довільна функція змінної .

Інтегруємо обидві частини по

де і – довільні двічі диференційовні в розглядуваній області функції. Повертаючись до змінних отримаємо Це і буде загальним розв’язком заданого рівняння.

Приклад 1.3 Знайти загальний розв’язок рівняння, звівши його до канонічного виду

.

Тут . Отже, задане рівняння параболічного типу.

Запишемо рівняння характеристик .

Поділивши на , отримаємо .

Знайдемо . .

Звідси .

Введемо заміну змінних: .

За другу нову змінну візьмемо, наприклад, (очевидно, що і незалежні).

Знайдемо всі частинні похідні, що входять у задане рівняння, виразивши їх через :

;

;

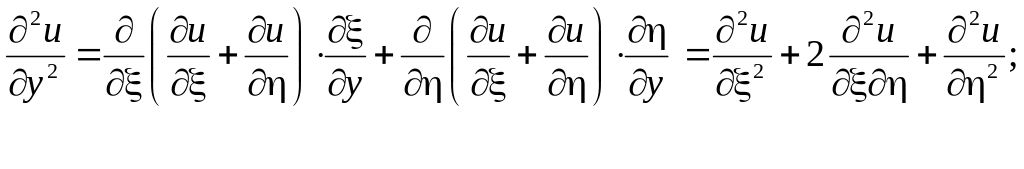
Підставивши у задане рівняння, після спрощень отримаємо .

Інтегруємо двічі по змінній :

, ,

де – довільні функції змінної .

Повертаючись до змінних отримаємо . Це і буде загальним розв’язком заданого рівняння.

Приклад 1.4 Звести до канонічного виду рівняння

.

Тут . Отже, задане рівняння еліптичного типу.

Запишемо рівняння характеристик .

Поділивши на , отримаємо .

Знайдемо .

.

Звідси

Введемо заміну змінних:

– один із загальних інтегралів, другий буде спряженим до нього;

Тоді , .

Знайдемо всі частинні похідні, що входять у задане рівняння, виразивши їх через :

;

;

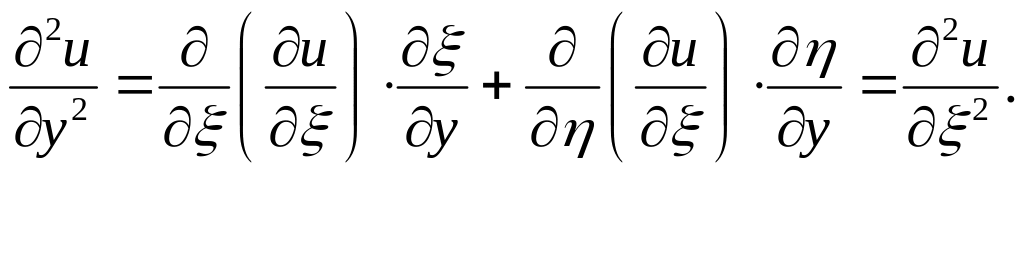
Підставивши у задане рівняння, після спрощень отримаємо його у канонічному виді:

.

Зауваження: наведена класифікація лінійних рівнянь зі сталими коефіцієнтами переноситься і на рівняння зі змінними коефіцієнтами, які в нашому посібнику не розглядаються.