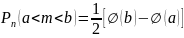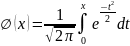Теорема гипотез (формула Бейеса)
До сих пор мы рассматривали вероятности событий до испытаний, т.е. в комплексе условий не фигурировал результат проведения опыта.
Решим
следующую задачу: Имеется полная группа
несовместных гипотез
.
Известны вероятности каждой из гипотез
.
Производится опыт и в его результате
осуществляется некоторое событие А,
вероятности которого по каждой из
гипотез известны
.
Найти какие вероятности меют гипотезы
в
связи с появлением события А, т.е. найти
условные вероятности
.
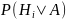Теорема гипотез:
Верояность гиопотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события:
Доказательство:
На основании аксиомы умножения вероятностей
Разрешая
это уравнение относительно
.
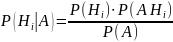Выражая P(A) получим (1) ч.т.д.
Если
все гипотезы
до
испытания имеют одинаковую вероятность,
т.е.
,
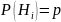то формула Бейеса принимает вид :
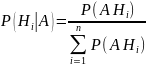
Лекция №3 26.02.13
Случайные величины
События являются качественной характеристикой случайного результата опыта. Случайный результат можно характеризовать и количественно. Количественной характеристикой случайного результата опыта является случайная величина.
Случайная величина – это величина, которая в результате опыта может принять то или иное, но только одно значение, причем заранее до опыта неизвестно, какое именно.
Случайные
величины обозначаются обычно заглавными
буквами конца латинского алфавита
(X,Y,Z,W…),
а их возможные значения малыми буквами
{
}.
Среди
случайных величин можно выделить 2
основных типа:
дискретные случайные величины (величина, число возможных значений которой либо конечно либо бесконечно, но четное множество)
непрерывные случайные величины
Случайная величина является абстрактным выражением случайного события. Каждое событие А можно связать некоторую характеристическую случайную величину.
Повторение испытаний. Формула Бернулли.
Пусть производится несколько испытаний, в результате которых может появиться событие А с определенной вероятностью. Если вероятность А в каждом испытании не зависит от исходов других испытаний, то такие испытания – независимые относительно события А.
Пусть требуется определить вероятность того, что в результате проведения n независимых испытаний некоторое событие А наступит ровно m раз, если в каждом из этих испытаний данное событие наступает с постоянной вероятностью Р(А)=p. Определить вероятность того, что в результате n независимых испытаний некоторое событие А наступит ровно m раз, если в каждом из этих испытаний событие наступает с постоянной вероятностью.
Решение:
Искомую вероятность будем обозначать
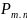или
.
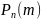Непосредственное применение теорем
сложения и умножения вероятностей для
решения поставленной задачи с увеличением
числа испытаний, приводит к очень
грамостким вычислениям, поэтому возникает
необходимость применения менее долгоемких
способов расчета. Один из таких способов
основан на применении формулы Бернулли.
Вывод формулы Бернулли:
Предположим,
в одинаковых условиях производится n
незавсимых
испытаний, результатом каждого из
которых может быть наступление события
А
с
вероятностью P(A)=p
либо
ему противоположного
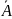c вероятностью P(
)=1-p.
Обозначим
через
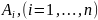наступление события А
в i-том
испытании. В силу постоянства условий
испытания:
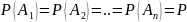
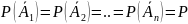
Вероятность
того, что событие А
при n
испытаниях
наступает ровно m
раз,
а в оставшихся n-m
испытаниях
наступит ему противоположное
.
При
этом событие А
в n
испытаниях
может появиться ровно m
раз
в разных последовательностях, число
которые равно
.
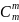Событие В – это событие, при котором событие А наступит ровно m раз
По условию испытания независимы. Это значит, что независимые события, входящие в эту комбинацию, поэтому используюется теорема умножения для независимых событий, получим:
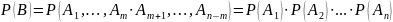
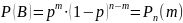
Т.к. все комбинации событий подобные комбинации В являются несовместными событиями и нам безразлично в какой именно последовательности появится событие А и в какой именно последовательности появится , то применяя теорему сложения вероятностей:
-
Формула
Бернулли
Формула Бернулии применяется в задачах, связанных с повторением опыта при одинаковых условиях. Т.к. события, состоящие в различном числе появления А в серии из n испытаний несовместны и образуют полную группу, то сумма вероятностей из n по m
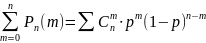
Биноминальное распределение позволяет ввести для вычисления вероятностей возможно числа наступлений события А серии из n независимых испытаний, так называемую, производящую функцию:
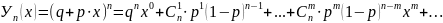
Эта
функция обладает тем свойством, что
коэффициент при
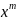в этом разложении равен вероятности
наступления события А
ровно m
раз
из n
независимых
испытаний, проводимых в постоянных
условиях.
Если условия переменны:
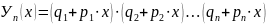
Наивероятнейшим
числом
появления события А
в n
независимых
испытаниях называется число, для которого
вероятность
превышает n
по
крайней мере не меньше вероятности
каждого из остальных возможных исходов.
Следствие из формулы Бернулли:
