
- •Скобцов ю.А. «эволюционные вычисления»
- •3 Источника эволюционных вычислений
- •Генетические алгоритмы
- •Генетические операторы Репродукция
- •Оператор кроссинговера(скрещивания)
- •Мутация
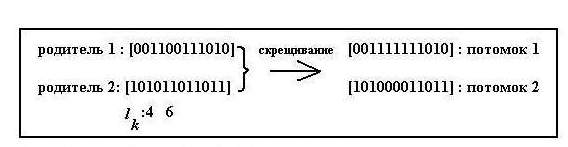
- •Простой пример
- •Репродукция
- •Представление вещественных решений в двоичной форме
- •Пример функции с популяцией особей в начале эволюции
- •«Конденсация» особей в окрестностях эксремумов
- •Положение особей популяции в конце эволюции
- •Использование кода Грея в га
- •1.8.1 Концептуальная простота
- •1.8.2 Широкая применимость
- •1.8.3 Меньшие требования при решении реальных задач
- •1.8.4 Потенциальное использование априорных знаний и гибридизация с другими методами
- •1.8.5 Параллелизм.
- •1.8.6 Устойчивость к динамическим изменениям
- •1.8.7 Способность к самоорганизации
- •1.8.8 Решение проблем, которые не имеют опыта решений
- •1.8.9 Недостатки га
- •Га для задач комбинаторной оптимизации Задача о покрытии
- •Задача об укладке рюкзака
- •Модификации и обобщения га
- •Пример двухточечного кроссинговера
- •Пример четырехточечного кроссинговера
- •1. Дискретная рекомбинация
- •Промежуточная рекомбинация
- •Мутация над вещественными числами
- •Генетические алгоритмы с изменяемой мощностью популяций
- •Параллельные генетические алгоритмы
- •Генетическое программирование
- •Усекающая мутация
- •Растущая мутация
- •Мутация «Обмен поддеревьев»
- •Фитнесс-функция в генетическом программировании
- •Применение эволюционных вычислений
- •С основами эволюционных вычислений можно ознакомиться в следующей книге:
Задача об укладке рюкзака
Эта
задача имеет следующую неформальную
простую постановку. Имеется рюкзак
объемом
![]() и
и
![]() различных предметов. Каждый предмет
различных предметов. Каждый предмет
![]() имеет известный объем Wi
и стоимость
Pi
(
имеет известный объем Wi
и стоимость
Pi
(![]() ).
В рюкзак можно положить целое число
различных предметов. Нужно упаковать
рюкзак так, чтобы полная стоимость
уложенных предметов была максимальной,
а их общий объем не превышал заданный
объем С – емкость рюкзака. Форма предметов
здесь не учитывается .
).
В рюкзак можно положить целое число
различных предметов. Нужно упаковать
рюкзак так, чтобы полная стоимость
уложенных предметов была максимальной,
а их общий объем не превышал заданный
объем С – емкость рюкзака. Форма предметов
здесь не учитывается .
Формальная постановка задачи: для данного множества весов Wi , стоимостей Pi и объема надо найти двоичный вектор X= (x1,…, xn), где xi=1 , если предмет укладывается в рюкзак;xi=0, если предмет не укладывается;
при
этом должно выполняться:
![]() ,
и
,
и
![]() .
.
Так
как решение задачи можно представить
двоичным вектором X=
(x1,…,
xn),
то очевидно при его поиске можно применить
простой ГА со стандартными операторами
скрещивания и мутации. Но при этом, что
на каждом шаге надо следить за тем,
чтобы новые решения, полученные в
результате скрещивания или мутации,
удовлетворяли требуемому ограничению
V![]() .
В случае невыполнения ограничения
«неправильное» потенциальное решение
должно быть уничтожено, что ведет к
сокращению популяции.
.
В случае невыполнения ограничения
«неправильное» потенциальное решение
должно быть уничтожено, что ведет к
сокращению популяции.
В
качестве фитнесс-функции в простейшем
случае можно взять
![]() ,
но в этом случае, как указано выше, есть
проблемы с неправильными решениями.
,
но в этом случае, как указано выше, есть
проблемы с неправильными решениями.
Модификации и обобщения га
Каждый из функциональных блоков ГА рис.1может быть реализован различными способами.
В настоящее время разработаны различные методы:
генерации начальной популяции;
отбора родителей;
генетических операторов скрещивания и мутации;
сокращения популяции и т.д.
процесса эволюции.
Приведем только несколько примеров:
Многоточечный кроссинговер
Разработаны различные обобщения классического одноточечного кроссинговера. Например, при двухточечном кроссинговере потомки наследуют фрагменты хромосом родителей между двумя случайно выбранными точками скрещивания, как это, например, показано на следующем рисунке.
Пример двухточечного кроссинговера
Графически это пример удобно представить в следующем виде.
Пример двухточечного кроссинговера

Многоточечный кроссинговер с большим четным количеством точек скрещивания графически удобно представить для хромосом в виде «колец», что показано на рисунках. При этом хромосома рассматривается как замкнутое кольцо, а точки скрещивания выбираются с равной вероятностью по всей его окружности.
Пример четырехточечного кроссинговера

Скрещивание (рекомбинация) действительных значений
При этом хромосома представляется действительными (вещественными) числами.
1. Дискретная рекомбинация
Этот вид скрещивания определен над векторами, компонентами которых являются вещественные числа. Рассмотрим на примере двух особей, соответствующие вектора которых имеют три целых значения. Для каждой переменной (позиции) значение переменной выбирается из первого или второго родителя с равной вероятностью. Пример выполнения этого оператора показан на рис. Здесь образцы (маски) показывают принадлежность данной компоненты потомка определенному родителю. Отметим, что этот тип рекомбинации применим к значениям любого типа.
-
1-й родитель
12
25
5
2-й родитель
123
4
34
1-й образец (маска)
2
2
1
2-й образец(маска)
1
2
1
1-й потомок
123
4
5
2-й потомок
12
4
5
