Контрольні запитання
4.1 У чому полягає особливість постановки для розв’язування задачі про поздовжні коливання стержня?
4.2 У чому полягає суть методу Фур’є для розв’язування задач про поздовжні коливання стержня?
4.3 При яких граничних умовах працює метод Фур’є?
Практичне заняття № 5
Тема: Постановка і розв’язання задач нестаціонарної теплопровідності
Основні теоретичні відомості
Постановка задачі про поширення тепла в стержні складається з рівняння теплопровідності, початкової та гра-ничних умов.
Рівняння теплопровідності для стержня має вигляд
де
– температура в будь-якому перерізі х
в
будь-який момент часу t,
k
–
коефіцієнт внутрішньої теплопровідності,
C
– питома теплопровідність,
– густина.
Початкова умова характеризує початковий розподіл тем-ператур в стержні:
.
Граничні
умови відображають тепловий режим на
кінцях стержня
.
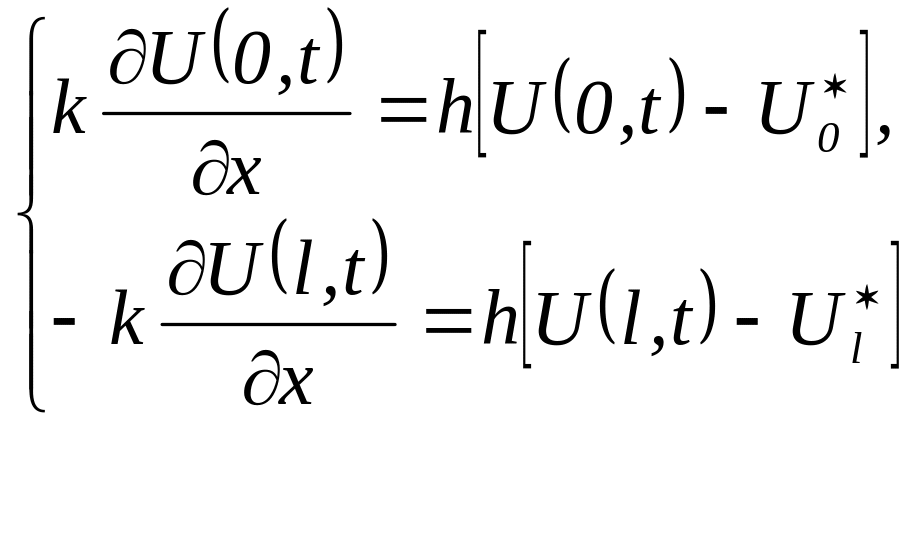Тут
h
–
коефіцієнт
теплообміну,
та
– температура навколишнього середовища
поблизу кінця
і
відпо-відно.
Окремі випадки:
1) На кінцях підтримується стала температура (у тому числі й нульова)
2) На одному кінці
(наприклад
)
підтримується ста-ла температура, а
другий кінець (
)
– теплоізольваний
3) На одному кінці ( ) підтримується стала темпера-тура, а на другому кінці ( ) відбувається вільний тепло-обмін з навколишнім середовищем
розв’язок задачі теплопровідності з однорідними гранич-ними умовами шукаємо за методом Фур’є.
1) Якщо Г.У.
то розв’язок має вигляд
де
2) Якщо Г.У.
то
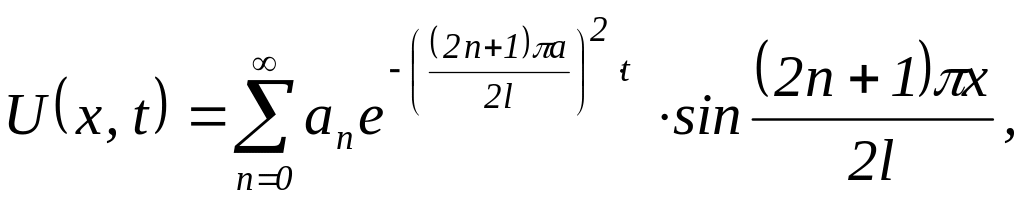
де
Порядок виконання роботи
5
.1
Поставити задачу математичної фізики
про поширен-ня тепла в стержні довжиною
l,
на
одно-му кінці якого
підтримується
стала температура
,
а
на другому
–
стала
температура
причому
.
Початковий розподіл температур задається
параболічним законом у вигляді графіка
(вершина параболи лежить на осі U).
5.2
Поставити і розв’язати задачу про
поширення тепла в стержні довжиною l,
якщо на кінцях стержня весь час
підтримується нульова температура, а
початковий розподіл температур задається
функцією
Поставимо
задачу
П.У.
Г.У.
Згідно з методом Фур’є розв’язок має вигляд
де
Унаслідок ортогональності системи функцій ненульовий розв’язок буде тільки при n=1. Отже,
Відповідь:
5.3 Поставити і розв’язати задачу про поширення тепла у стержні довжиною l, на одному з кінців якого підтримується нульова температура, а другий – теплоізольований. Початковий розподіл температур задається графічно:
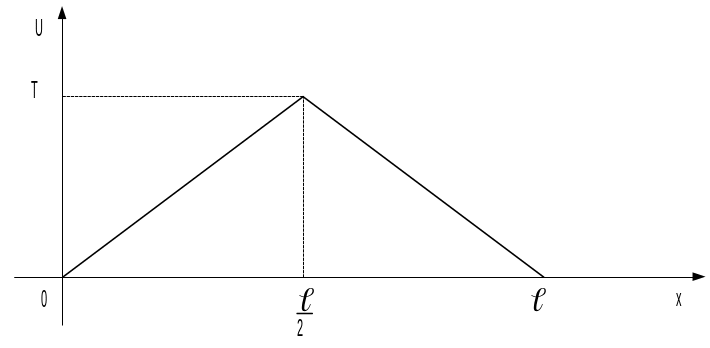
Поставимо задачу
П.У.
Г.У.
Згідно з методом Фур’є розв’язок має вигляд
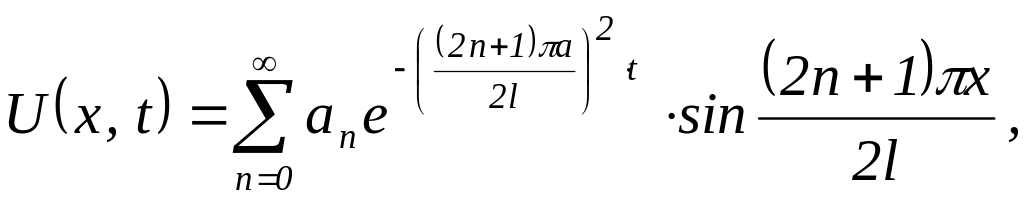де
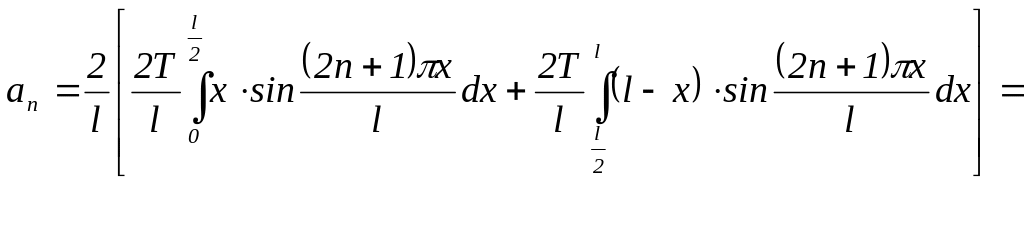
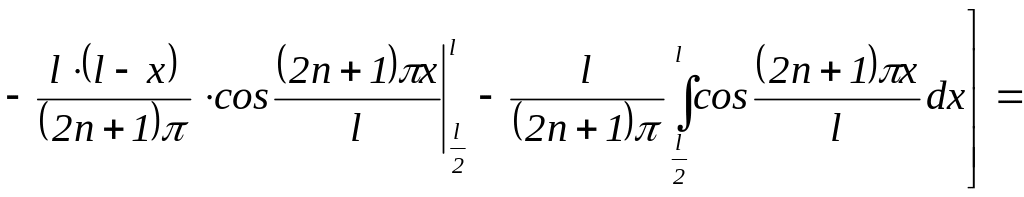
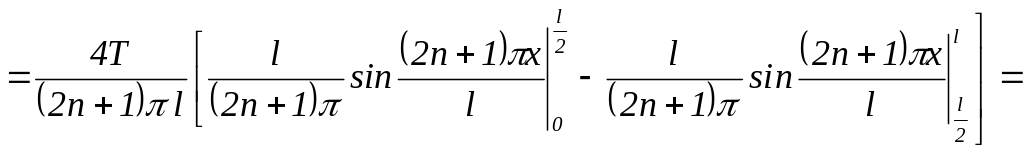
Відповідь:
Задачі для самостійного розв’язування
5.1 Поставити задачу математичної фізики про поширення тепла в стержні довжиною l, на одному кінці якого відбувається вільний теплообмін з навколишнім середовищем, температура якого поблизу цього кінця становить 20 °С, а другий кінець теплоізольований. Початковий розподіл температур задається графічно:
5.2 Поставити задачу математичної фізики про поширення тепла в стержні довжиною l, на одному кінці якого підтримується нульова температура, а на другому кін-ці стала температура Т. Початковий розподіл темпе-ратур задається параболічним законом (вершина параболи міститься в початку координат).
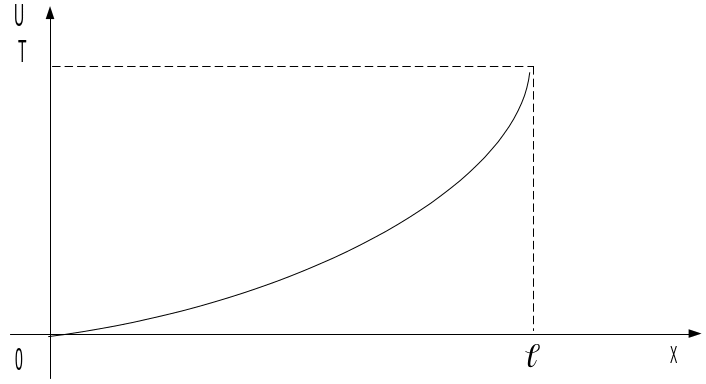
5.3 Поставити задачу
математичної фізики про поширення тепла
в стержні довжиною l,
на кінцях якого підтримується
нульова температура, а початковий
розподіл температур задається функцією
5.4 Поставити задачу математичної фізики про поширення тепла в стержні довжиною l, на одному кінці якого весь час підтримується нульова температура, а другий кінець теплоізольований. Початковий розподіл темпе-ратур задається графічно:
