Порядок виконання роботи
2.1 Поставити задачу про поздовжні коливання в стержні, один кінець якого жорстко закріплено, а до вільного кінця прикладено розтягуючу силу Р, причому у момент часу дія сили раптово припиняється.
.
Під
час дії сили на вільному кінці маємо
.
Про-
інтегрувавши це співвідношення по х
у межах від 0
до х,
отримаємо
Отже,
П.У.
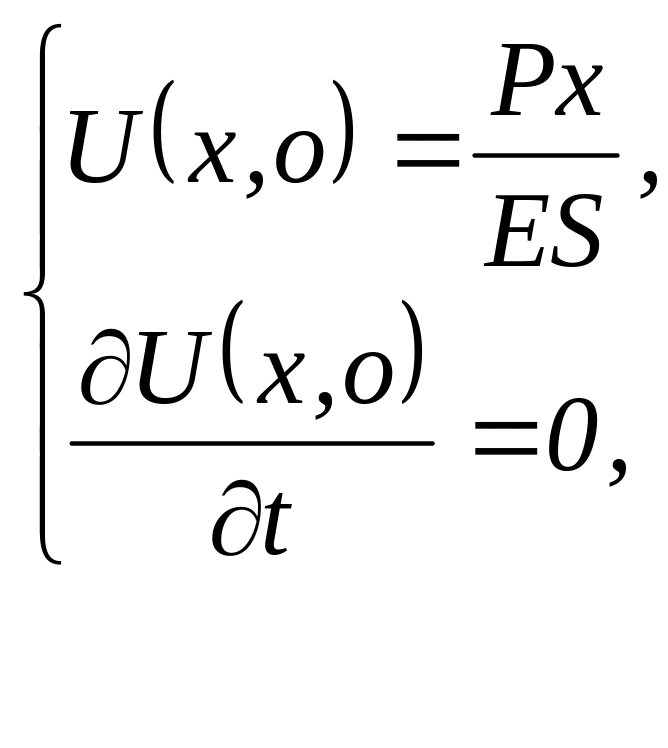Г.У.
2.2 Поставити задачу про поздовжні коливання в стержні довжиною l, один кінець якого жорстко закріплено. Стержень знаходиться у стані спокою. У момент часу до його вільного кінця прикладено силу Q напрямлену вздовж осі стержня.
П.У.
Г.У.
2.3 Поставити задачу про поздовжні коливання в стержні верхній кінець вертикально підвішеного важкого стержня прикріплений до стелі ліфта, який вільно падає, причому досягнувши швидкості v, він раптово зупиняється.
,
.
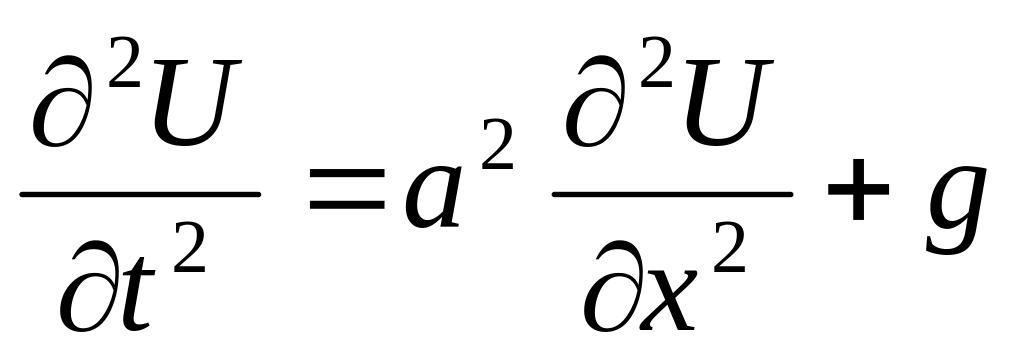П.У.
Г.У.
2.4 Поставити задачу про поздовжні коливання в стержні, один кінець якого x=0 закріплено нерухомо, а на кінці x=l має місце в’язкий опір. Стержень попередньо розтягнутий силою Q, дія якої у момент часу раптово припиняється.
, .
П.У.
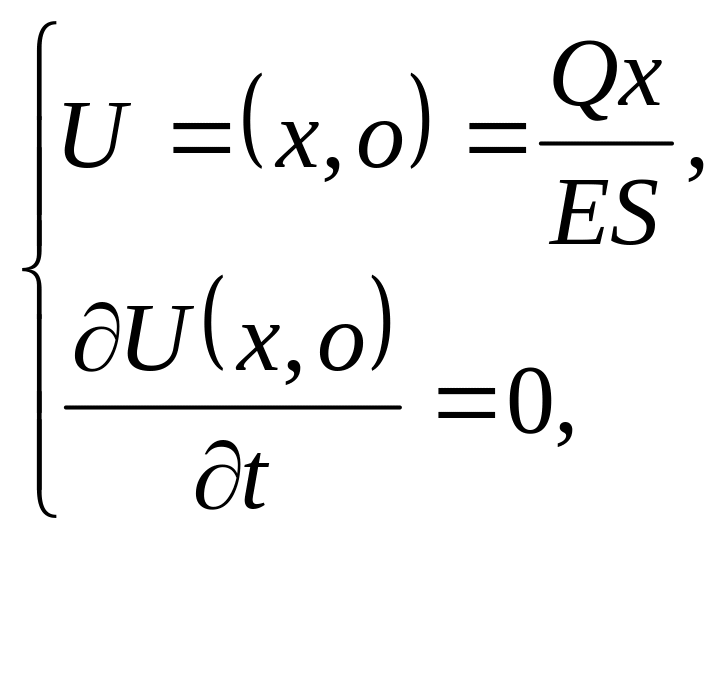Г.У.
2.5 Сформулювати задачу математичної фізики:
, .
П.У.
Г.У.
Це задача про поздовжні коливання стержня, один кінець якого жорстко закріплений, а до іншого кінця у момент часу прикладено силу At. Початкові деформації відсутні. Стержень знаходиться у стані спокою.
2.6 Сформулювати задачу математичної фізики:
, .
П.У.
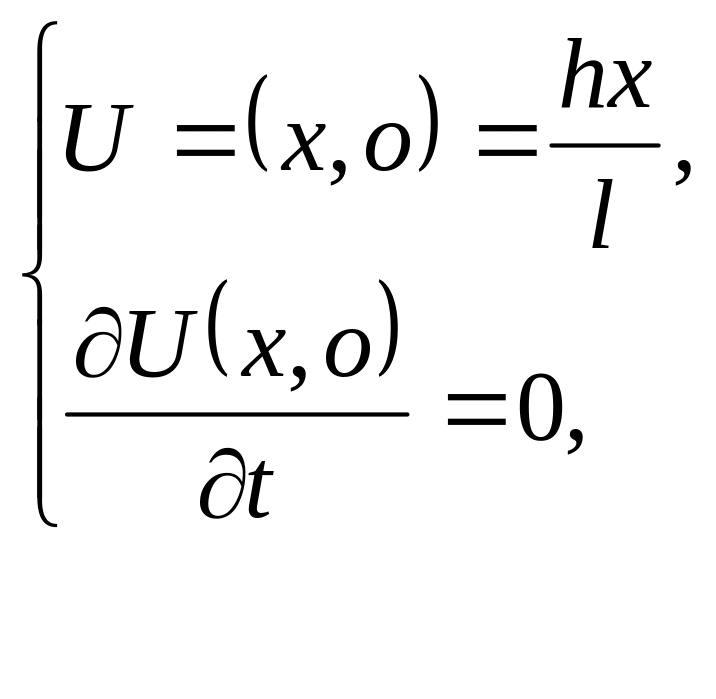Г.У.
Це задача про поздовжні коливання стержня, один кінець якого жорстко закріплений, а на другому зосереджено вантаж масою М. Стержень попередньо був розтягнутий на величину h (якоюсь силою, яку було знято). Стержень перебу-вав у стані спокою.
2.7 Поставити задачу про поперечні коливання струни з закріпленими кінцями, якщо у початковий момент часу вона перебувала у стані спокою і мала таку форму
П.У.
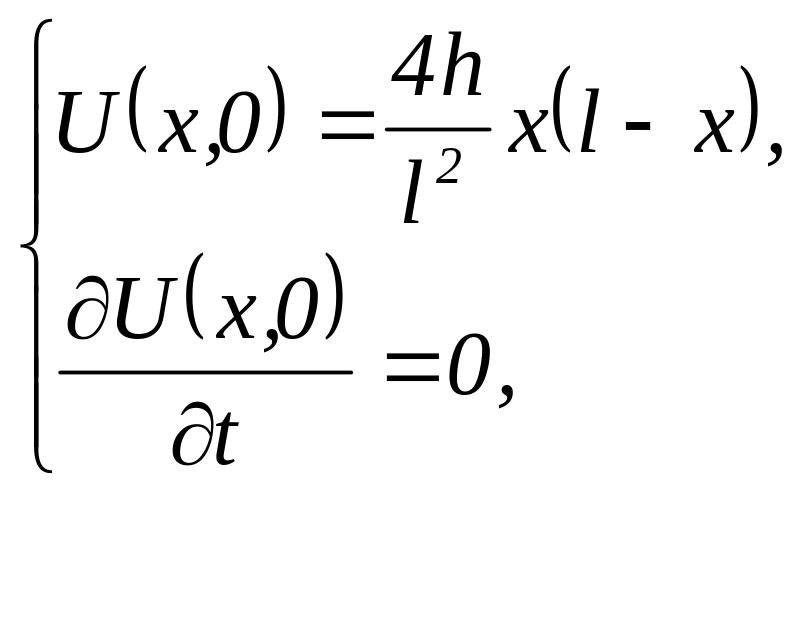Г.У.
2.8 Поставити задачу про поперечні коливання важкої струни з закріпленими кінцями, на яку в початковий момент часу починає діяти постійна сила, що дорівнює силі тяжіння.
П.У.
Г.У.
Оскільки про початкові швидкості точок струни в умові задачі нічого не говориться, то вважатимемо, що струна перебувала у стані спокою.
2.9 Поставити задачу про поперечні коливання струни з закріпленими кінцями, якщо у початковий момент часу зміщення точок струни дорівнює нулю, а швидкість точок струни були розподілені за законом, який задається графічно.
.
П.У.
Г.У.
2.10 Поставити задачу про поперечні коливання нескінченної струни, якщо у початковий момент часу t=0 струна перебувала у стані спокою і мала таку початкову форму:
.
П.У.
