Зміст

Вступ...............................................................................................4

Практичне заняття №1 Повторення деяких розділів вищої математики..............................................……….....................…..5

Практичне заняття №2 Постановка задач про поздовжні коли-вання в стержні та поперечні коливання стру-ни..............................................................................................… 13

Практичне заняття №3 Методи розв’язання задач про попе-речні коливання струни ...................................……….……… 25

Практичне заняття №4 Метод Фур’є для розв’язання задач про поздовжні коливання у стержні. Контрольна робота з теми «Постановки задач математичної фізики на коливання та методи їхнього розв’язання» ................................................36

Практичне заняття №5 Постановка і розв’язання задач неста-ціонарної теплопровідності...................................................….51

Практичне заняття №6 Стаціонарні процеси. Рівняння Лапла-са....................................................................................................59

Практичне заняття №7 Застосування операційного числення при розв’язуванні диференціальних рівнянь з частинними по-хідними.........................................................................................65

Індивідуальні розрахунково-графічні роботи з математичної фізики............................................................................................76

Перелік використаних джерел…………….…………......….. 121

Вступ

Практикум призначено для студентів вищих технічних за-кладів з метою ознайомлення з такими спеціальними розділа-ми математики як „Рівняння математичної фізики” та „опера-ційне числення”.

Дану методичну розробку виконано відповідно з навчаль-ною програмою дисципліни „Вища математика”, яка передба-чена навчальним планом підготовки бакалаврів за напрямом „Нафтогазова справа”.

Практикум допоможе студентам самостійно опанувати розв’язання типових задач з математичної фізики та операцій-ного числення, базуючись лише на знаннях з курсу вищої ма-тематики та загальної фізики.

Практичне заняття №1

Тема: Повторення деяких розділів вищої математики:

а) знаходження аналітичного виразу функції за її гра-

фіком;

б) диференціальні рівняння зі сталими коефіцієнтами;

в) диференціальні рівняння з частинними похідними.

Основні теоретичні відомості

– рівняння прямої на площині, заданої

двома точками та ; – рівняння прямої з кутовим коефіцієнтом.

– квадратична парабо-ла, де та – точки перетину з віссю абсцис; в точці з координатами графік функції перетинає вісь ординат; рівняння, що задає вісь симетрії; при вітки па-раболи спрямовані вверх, а при – вниз.

– гармонічне коливання за законом си-нуса, – за законом косинуса, де – ампулі-туда, що прямопропорційно впливає на розтяг графіка функції вздовж осі ординат; – фаза, що характеризує початкове змі-щення відносно початку координат по осі абсцис; – частота коливання, що оберненопропорційно впливає на розтяг графі-ка функції вздовж осі абсцис, причому період коливань зале-жить від частоти , .

– лінійне однорідне диференціальне рів-няння другого порядку (ЛОДР) зі сталими коефіцієнтами

Загальний розв’язок шукаємо за допомогою характеристично-го рівняння де

1) Якщо то корені та – різні, дійсні. Тоді загаль-ний розв’язок має вигляд .

2) Якщо то корені дійсні = = . Тоді загальний розв’язок має вигляд .

3) Якщо то корені – комплексноспряже-ні. Тоді загальний розв’язок (ЛОДР) матиме такий вигляд .

– лінійне неоднорідне диференціаль-не рівняння другого порядку (ЛНДР) зі сталими коефіцієнта-ми та спеціальною правою частиною. Якщо

,

де – відомий многочлен степеня – , – відомий многочлен степеня – , – корінь правої частини. Загальний розв’язок шукаємо у вигляді суми загального розв’язку ЛОДР і частинного розв’язку ЛНДР де – загальний розв’язок ЛОДР, – частинний розв’язок ЛНДР, який має вигляд , де ,

– два многочлени степе-ня n з невідомими коефіцієнтами , які знаходимо за методом невизначених коефіцієнтів, r – число співпадінь кореня правої частини з коренями .

Порядок виконання роботи

Приклад 1.1 Функція задана графічно на проміжку . Знайти її аналітичний вираз.

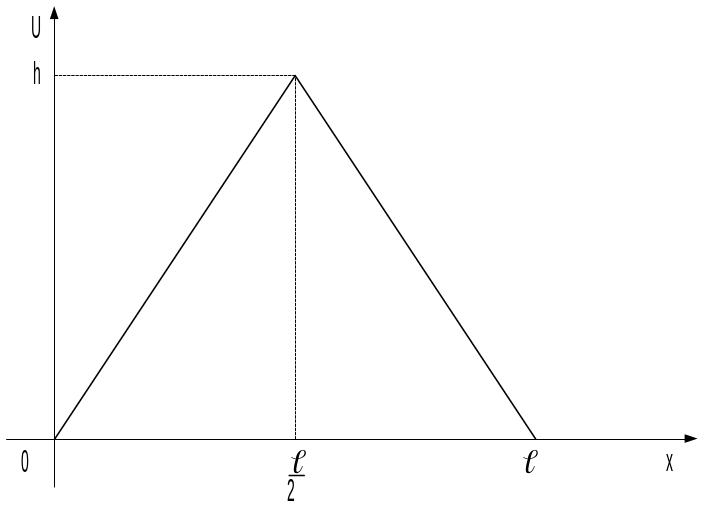
На проміжку функція U є відрізком прямої, що проходить через дві точки та . Звідси маємо:

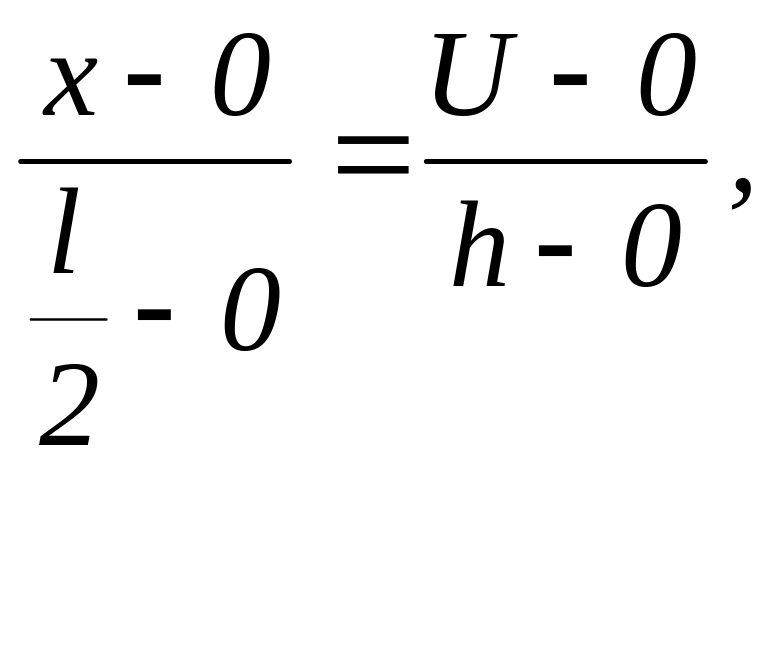
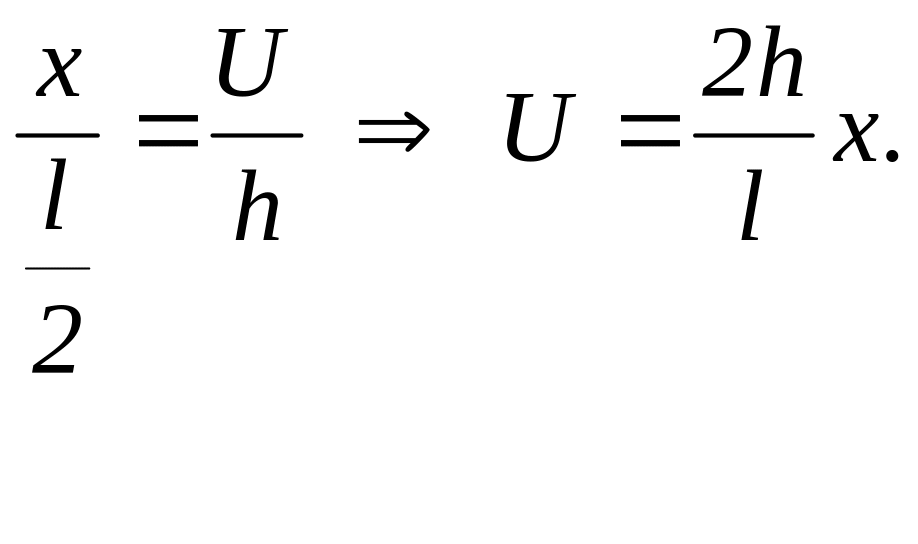
на проміжку функція u є також відрізком прямої, що проходить через дві точки та :

,

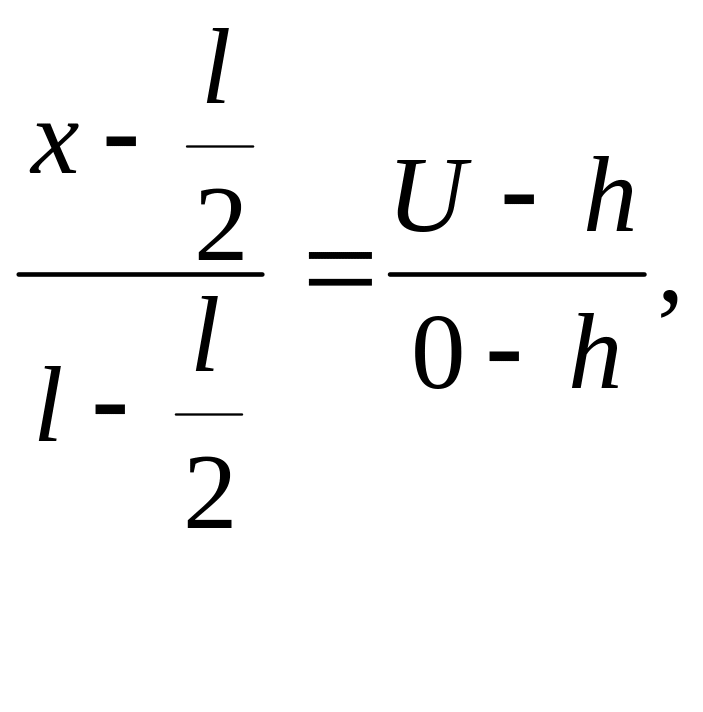
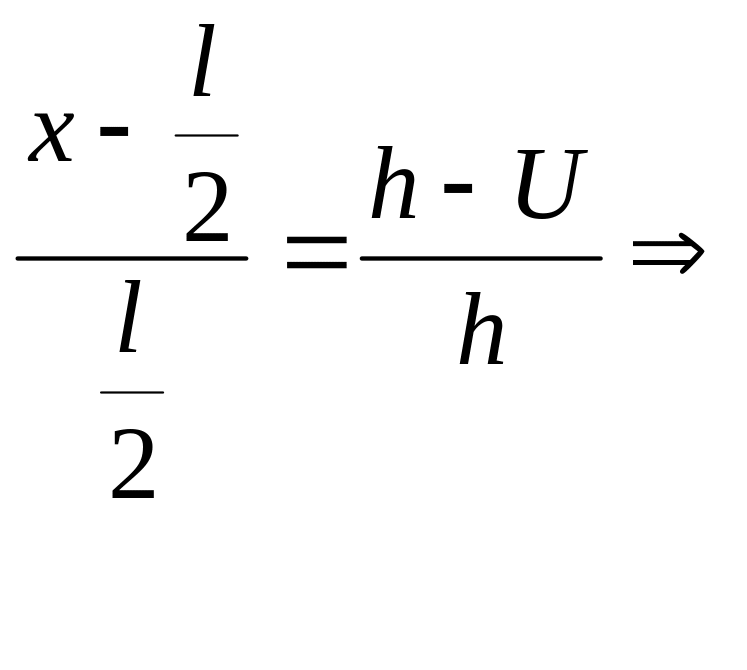
Отже,

Приклад 1.2 Функція задана графічно у вигляді частини параболи на проміжку . Знайти її аналітичний вираз.

, вітки параболи напрямлені вниз.

отже, ; , бо парабола проходить через початок координат, отже, ;

. Тоді , або .

Приклад 1.3 Функція задана графічно у вигляді півхвилі синусоїди на проміжку . Знайти її аналітичний вираз.

, А=h, Знайдемо частоту

Оскільки точка належить даній кривій, то А для одного періо-ду Отже, .

Приклад 1.4 Розв’язати диференціальне рівняння

Розв’яжемо характеристичне рівняння

звідки

Отже, .

Приклад 1.5 Розв’язати диференціальне рівняння

Загальний розв’язок шукатимемо у вигляді .

Знайдемо . Розв’яжемо характеристичне рівняння Отже,

Знайдемо . Оскільки , то тобто є одне співпадіння, отже, r=1, n=1.

Тоді .

Визначимо та , підставивши в задане рівняння.

, ,

,

.

Складемо систему, прирівнюючи коефіцієнти при однакових степенях х:

Таким чином, .

Загальний розв’язок даного рівняння

Приклад 1.6 Розв’язати задачу Коші

Характеристичне рівняння

Отже, загальний розв’язок

Для визначення довільних сталих знайдемо похідні

Складаємо систему згідно з початковими умовами:

Розв’язавши друге і третя рівняння, отримаємо ф із першого рівняння дістанемо

Розв’язок задачі Коші

Приклад 1.7 Розв’язати диференціальне рівняння з частинними похідними: .

Двічі інтегруємо по змінній у, при цьому x=const: , .

Приклад 1.8 Розв’язати диференціальне рівняння з частинними похідними: .

На першому етапі інтегруємо по змінній у при цьому x=const: , на другому – по змінній х при цьому у=const: .