2. Основные коэффициенты деформации при прокатке.

При продольной прокатке изменяются линейные размеры металла по толщине, ширине, длине. Степень деформации по этим трем главным направлениям будит оцениваться коэффициентами деформации.

1. коэффициент обжатия:

2. коэффициент уширения:

3. коэффициент вытяжки:

Установим связь между тремя коэффициентами прокатки пользуясь законом постоянства объема.

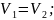
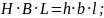
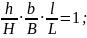
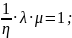
Таким образом коэффициент обжатия является максимальным из трех и равен произведению двух остальных.

Коэффициент вытяжки представим через отношения площадей поперечного сечения до и после прокатки для этого воспользуемся законом постоянства объема.

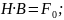
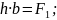
Коэффициент вытяжки, выраженный через площади поперечного сечения, прокатываемой полосы используются при составлении режима деформации на сортовых станах.

Обычно процесс формирования готового проката выполняется не через один пропуск, а за несколько, поэтому при составлении режима деформации необходимо знать частный, средний и общий коэффициент деформации.

Все профили проката условно делятся на 3 группы:

1. Простые сортовые профили.

К ним относится круг, квадрат, шестигранник и полоса.

2. Фасонные сортовые профили.

К ним относится рельсы, балки, швеллеры и т.д.

3. Листы, широкая полоса.

Этих профилей проката необходимо иметь набор соответствующих валков, ручьевых или гладких. Ручьевые валки при прокатки образуют калибры.

Калибром называют просвет между валками, образуемых ручьями двух или трех валков. Форма калибра определяет форму поперечного сечения прокатного профиля.

Общей вытяжкой называется коэффициент, характеризующий изменение величины поперечного сечения полосы за весь период проката.

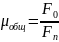
F₀ – площадь сечения заготовки до прокатки.

Fn – площадь сечения после прокатки.

Частной вытяжкой называется коэффициент, характеризующий изменение величины поперечного сечения за один пропуск.

Общий коэффициент вытяжки равен произведению частных коэффициентов вытяжки.

Если частные коэффициенты вытяжки будут равны между собой, то общий коэффициент вытяжки будет определяться:

При известных коэффициентов общего и среднего числа пропусков определяется:

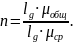
Тема № 2.2 Захват металла валками.

2.2.1 Силы, действующие при захвате металла валками.

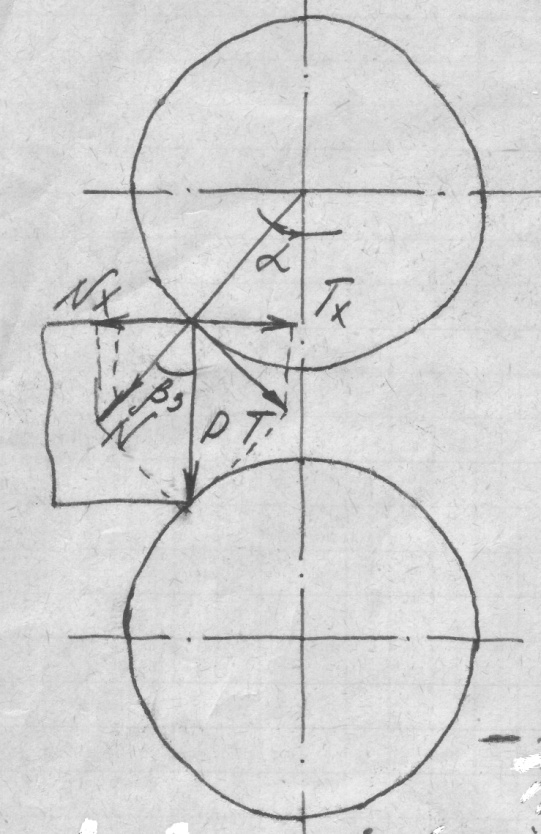При соприкосновении полосы с валками каждый (в точке касания с полосами) из них оказывает на полосу действие в виде силы N, направленной нормально к поверхности валка и силы трения T, направленной по касательной.

Сила трения определяется по формуле:

f₃ – коэффициент трения при захвате.

β₃ – угол трения при захвате, т.е. угол, тангенс которого равен f₃ .

Рассмотрим при каких условиях валки смогут захватить полосу и обеспечить ее движение (прокатку).

Рисунок 1. Схема действия сил в

начинающем моменте захвата

Проектируя силы N и T, действующие на полосу в момент соприкосновения её с валками на горизонтальную ось, получим силы Nx и Tx, действующие на полосу в противоположных направлениях.

Сила Tx – втягивает полосу в валки, а сила Nx – восстанавливает ее Рисунок 1.

Захват полосы валками произойдет при условии: Tx ≥ Nx.

следовательно

Подставим в уравнение (1) значение T, получим:

Сократив обе части неравенства на N и разделив на cosα получим условие захвата полосы валками:

Следовательно захват полосы валками произойдет только тогда, когда тангенс угла захвата будет меньше коэффициента трения, или когда угол захвата будет меньше угла трения.

Об условиях захвата можно судить по положению равнодействующей силы P. Отклонение этой силы от положения вертикали в сторону прокатки свидетельствует о том, что горизонтальная проекция втягивающей силы Tx больше горизонтальной проекции выталкивающей силы Nx и захват возможен.

В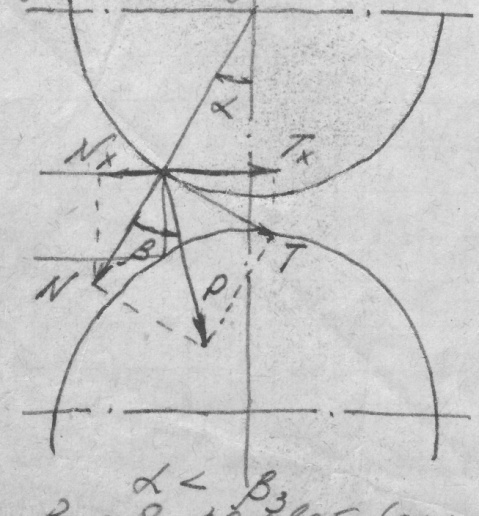 это случаем Рисунок 2.

При соотношении углов равнодействующая направлена от вертикали в сторону противоположную направлению прокатки, что свидетельствует о невозможности захвата полосы валками в данных условиях Рисунок 3.

Рисунок 2. Захват возможен.