Определение производной функции .
Пусть
в некоторой окрестности точки 
определена функция 
Производной
функции 
в
точке 
называется предел,
если он существует,
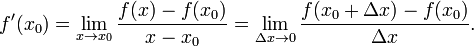
Общепринятые обозначения производной функции в точке
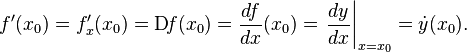
2*.Определение касательной и нормали к графику функции y=f(x). Геометрический смысл производной. Уравнение касательной и нормали к графику кривой y=f(x).
Геометрический смысл производной
Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение x 0, причем x+ x (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+ x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+ x,f(x+ x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОXчерез ( x).
Определение . Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при x 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.
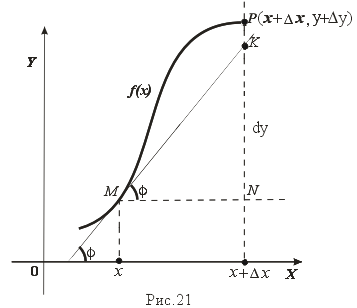
Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел lim x 0 ( x) = 0, который равен углу, образованному касательной с положительным направлением оси OX.
Справедливо утверждение:
Предложение 1. Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x).
Из этого утверждения вытекает геометрический смысл производной: производная f'(x0) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x0, который в свою очередь равен tg угла наклона касательной к графику функции.
Тогда уравнение касательной к кривой f(x) в точке x0 имеет вид
y = f(x0)+f'(x0)(x-x0)
Уравнение нормали
Нормаль -- это перпендикуляр к касательной (см. рисунок). Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к. угол наклона нормали -- это угол β1, то имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка (x0,f(x0))∈ нормали, уравнение примет вид:
y−f(x0)=−1f/(x0)(x−x0).