Определение

Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке  , где  , если её плотность   имеет вид:

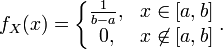
Пишут:  . Иногда значения плотности в граничных точках   и   меняют на другие, например   или 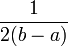 . Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.

Функция распределения

Интегрируя определённую выше плотность, получаем:

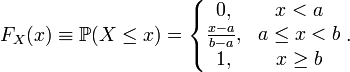
Так как плотность равномерного распределения разрывна в граничных точках отрезка  , то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:

.

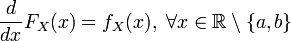Числовые характеристики:  ,  , 

32.Биноминаьное распределение,его числовые характеристики.

Биномиальное распределение - распределение количества «успехов» в последовательности из   независимых случайных экспериментов, таких что вероятность«успеха» в каждом из них постоянна и равна  .

 - количество «успехов» в последовательности из   независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна  .  .

Закон распределения   имеет вид:

	0	1	…..	k	…..

Здесь вероятности находятся по формуле Бернулли:  .

Характеристики:  ,  , 

34.Нормальное распределение: плотность вероятности,ее график. Числовые характеристики нормального распределения. Формулы нахождения вероятности попадания нормально распределенной случайной величины в произвольный интервал и в интервал симметричный относительно математического ожидания. Правило 3-х сигм.

Нормальное распределение или распределение Гаусса (непрерывное)

Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Плотность распределения:

Числовые характеристики:  ,  , 

Пример плотности распределения:

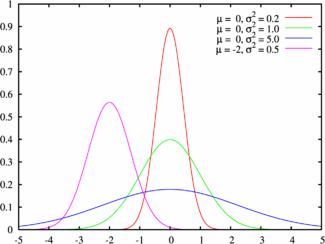
Нормальный закон распределения случайной величины с параметрами   и  называется стандартным или нормированным, а соответствующая нормальная кривая - стандартной или нормированной.

Функция Лапласа  .

Вероятность попадания нормально распределенной случайной величины   в заданный интервал 

Вероятность отклонения нормально распределенной случайной величины   на величину   от математического ожидания (по модулю).

.

Правило трёх сигм ( ) — практически все значения нормально распределённой случайной величины лежат в интервале  . Более строго — не менее чем с 99,7 % достоверностью значениенормально распределенной случайной величины лежит в указанном интервале (при условии, что величина  истинная, а не полученная в результате обработки выборки).

Если же истинная величина   неизвестна, то следует пользоваться не  , а s. Таким образом, правило трёх сигм преобразуется в правило трёх s.

1*. Приращение функции одной переменной. Определение производной функции одной независимой переменной.

Приращение функции – разность между двумя значениями функции.

1. Функция одной переменной. Пусть задана функция у = f(x), определенная при значении аргумента, равном х₀. Дадим аргументу приращение х, т.е. рассмотрим значение аргумента, равное x₀ + х. Предположим, что это значение аргумента также входит в область определения данной функции. Тогда разность y = f(x₀ + х) – f(x₀) называется приращением функции.