25. Случайные величины. Дискретная случайная величина. Закон распределения дискретной случайной величины. Функция распределения дискретной случайной величины.

Случайной называется величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента

Дискретной назовём случайную величину, возможные значения которой образуют или конечное множество, или счётное (бесконечное множество, элементы которого можно пронумеровать).

Назовём законом распределения дискретной случайной величины правило, по которому каждому возможному значению ставится в соответствие вероятность, с которой случайная величина может принять это значение.

Х	х1	х2	х3	x4	…	xn
Р	p1	p2	p3	p4	…	рn

Назовём функцией распределения функцию, равную вероятности того, что случайная величина примет значение, меньше .

26. Непрерывная случайная величина. Функция распределения случайной величины (определение). Свойства функции распределения (с доказательством одного из свойств).

26.Непрерывная случайная величина. Функция распределения случайной величины (определение). Свойства функции распределения (с доказательством одного из свойств).

Случайную величину назовем непрерывной, если ее функция распределения непрерывна.

Функцией распределения называют функцию , определяющую вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х, т.е.

F(x)=P(X<x)

Функция распределения F(x) обладает следующими свойствами:

1) Функция распределения F(x) не убывает: если х₁<x₂, то F(x₁)≤F(x₂)

2) Существуют пределы и

3) Функция распределения F(x) непрерывна слева:

Доказательство первого свойства.

Для любых чисел x₁<x₂ событие {ξ<x₁} влечёт событие {ξ<x₂} , т.е {ξ<x₁} {ξ<x2} . Но вероятность — монотонная функция событий, поэтому

27.Нахождение вероятности попадания непрерывной случайной величины в данный интервал (с выводом).

28. Плотность вероятности, определение, свойства. Нахождение вероятности попадания случайной величины в данный интервал. Нахождение функции распределения по известной плотности (вывод формулы).

Плотность вероятности случайной величины X - такая функция р(х) > 0. что вероятность неравенства а < X < b (при любых а и b) равна интеграл ; ф-ция р(х) должна удовлетворять при этом условию:

Свойства плотности вероятности.

1.Плотность вероятности определена почти всюду. Если f является плотностью вероятности P и f(x)=g(x) почти всюду относительно меры Лебега, то и функция g также является плотностью вероятности P .

2. Интеграл от плотности по всему пространству равен единице:

3. Замена меры в интеграле Лебега.

Для вычисления этой вероятности воспользуемся общей формулой

P(a<X<b)=F(b)-F(a)

29. Вероятностный смысл плотности. Элемент вероятности.

30. Математическое ожидание дискретной и непрерывной случайной величины, определения. Свойства математического ожидания с доказательством одного из них.

Математическое ожидание — среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей

Свойства.

.

31. Дисперсия случайной величины, определение. Докозательство одного из них. Среднеквадратичное отклонение, определение .

Дисперсия случайной величины — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается 

Свойства

• Дисперсия любой случайной величины неотрицательна: 

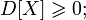
• Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;

• Если случайная величина равна константе, то её дисперсия равна нулю: 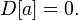  Верно и обратное: если 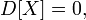  то 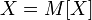  почти всюду;

• Дисперсия суммы двух случайных величин равна:

, где   — их ковариация;

• Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:

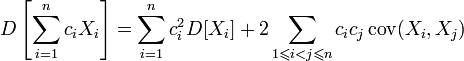, где  ;

• В частности,   для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;

• 

• 

• 

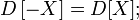
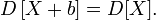
• Среднеквадратичное отклонение— в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно еёматематического ожидания.

33.Равномерное распределение, его числовые характеристики, функция распределения.

Равномерное распределение — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.