- •14. Разложение в тригонометрический ряд Фурье функции, заданной на интервале [-π: π]. Вид ряда, формулы для коэффициентов с выводом одной из них.
- •16. Ряд Фурье для чётных и нечётных функций: вид ряда, формулы для коэффициентов ( с обоснованием).
- •17. Разложение в ряд Фурье функции, заданной на произвольном интервале, вид ряда, формулы для коэффициентов, сходимость к порождающей функции.
- •19. Случайные события. Классификация событий по возможности их появления: достоверное, невозможное, совместные и несовместные события.
- •21. Теорема сложения вероятностей для совместных и несовместных событий с доказательством.
- •22. Условная вероятность. Независимые события. Теорема умножения вероятностей для зависимых и независимых событий.
- •23. Полная группа событий. Формула полной вероятности (с выводом). Формула Байеса (с выводом).
- •24. Испытания Бернулли. Формула Бернулли (с выводом). Локальная и интегральная формулы Муавра-Лапласа, Функция Лапласа. Простейший поток событий. Формула Пуасона.
- •25. Случайные величины. Дискретная случайная величина. Закон распределения дискретной случайной величины. Функция распределения дискретной случайной величины.
- •26. Непрерывная случайная величина. Функция распределения случайной величины (определение). Свойства функции распределения (с доказательством одного из свойств).
- •26.Непрерывная случайная величина. Функция распределения случайной величины (определение). Свойства функции распределения (с доказательством одного из свойств).
- •27.Нахождение вероятности попадания непрерывной случайной величины в данный интервал (с выводом).
- •28. Плотность вероятности, определение, свойства. Нахождение вероятности попадания случайной величины в данный интервал. Нахождение функции распределения по известной плотности (вывод формулы).
- •29. Вероятностный смысл плотности. Элемент вероятности.
- •30. Математическое ожидание дискретной и непрерывной случайной величины, определения. Свойства математического ожидания с доказательством одного из них.
- •Определение
- •Функция распределения
- •Определение производной функции .
- •Общепринятые обозначения производной функции в точке
- •Геометрический смысл производной
24. Испытания Бернулли. Формула Бернулли (с выводом). Локальная и интегральная формулы Муавра-Лапласа, Функция Лапласа. Простейший поток событий. Формула Пуасона.
Схема Бернулли
Рассмотрим
стохастический эксперимент, который в
свою очередь является последовательностью
n
независимых и однородных (одинаковых)
испытаний, в результате каждого из
которых может произойти событие
или ему противоположное
с вероятностями
 и
и
 По условию результат любого испытания
не зависит от его порядкового номера и
от того, что произошло до него. Найдём
вероятность
По условию результат любого испытания
не зависит от его порядкового номера и
от того, что произошло до него. Найдём
вероятность
 события
события
 ,
заключающегося в том, что в результате
событие
появится ровно
,
заключающегося в том, что в результате
событие
появится ровно
 раз. Очевидно, интересующее нас событие
появится тогда, когда появится одно из
следующих событий:
раз. Очевидно, интересующее нас событие
появится тогда, когда появится одно из
следующих событий:

Здесь
выписаны все комбинации из
 сомножителей,
из которых
множителей
вида
и
сомножителей,
из которых
множителей
вида
и
 вида
.
Нижний индекс указывает на порядковый
номер испытания. Поскольку
произойдёт тогда, когда произойдёт или
первая, или вторая, …, или последняя
комбинация, то
вида
.
Нижний индекс указывает на порядковый
номер испытания. Поскольку
произойдёт тогда, когда произойдёт или
первая, или вторая, …, или последняя
комбинация, то

В
этой сумме имеется всего
 (или
(или
 )
таких комбинаций, поскольку
элементов типа
(или
элементов типа
)
распределяются по
позициям.
Поскольку все слагаемые в этой сумме
попарно несовместны, а множители в
каждом слагаемом независимы, то искомая
вероятность будет равна сумме одинаковых
слагаемых, каждое из которых содержит
множителей
)
таких комбинаций, поскольку
элементов типа
(или
элементов типа
)
распределяются по
позициям.
Поскольку все слагаемые в этой сумме
попарно несовместны, а множители в
каждом слагаемом независимы, то искомая
вероятность будет равна сумме одинаковых
слагаемых, каждое из которых содержит
множителей
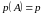 и
множителей
и
множителей
 .
Учитывая, что всего слагаемых
,
в итоге получаем формулу Бернулли:
.
Учитывая, что всего слагаемых
,
в итоге получаем формулу Бернулли:
 (1.15)
(1.15)
Локальная и интегральная формулы Муавра-Лапласа
При
достаточно большом n
и не слишком малых p
и q
формула Пуассона уже даёт значительную
погрешность и применяется другое
приближение – формула Муавра - Лапласа,
которую можно получить из формулы
Бернулли, совершая предельный переход
и применяя формулу Стирлинга для
вычисления

 где
где
 и
и
 (1.21)
(1.21)
Эта
формула также табулирована (Таблица
3), причём в силу чётности функции
 ,
таблица её значений составлена только
для
,
таблица её значений составлена только
для

Если
при сохранении условий предыдущего
пункта нас интересует вероятность того,
что при
испытаниях событие
появляется не менее
 и не более
и не более
 раз, то формула (1.18) с учётом предельного
перехода превращается в интегральную
формулу Муавра-Лапласа:
раз, то формула (1.18) с учётом предельного
перехода превращается в интегральную
формулу Муавра-Лапласа:

где

и
сумма превращается в интеграл. Функция
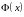 –
интеграл от
–
интеграл от
 –
называется функцией Лапласа и представляет
собой не выражающийся через элементарные
функции интеграл. Поскольку функция
Лапласа нечётная (
–
называется функцией Лапласа и представляет
собой не выражающийся через элементарные
функции интеграл. Поскольку функция
Лапласа нечётная ( )
и быстро приближается к своему
асимптотическому значению 0.5, то таблица
её значений (Таблица 4) составлена для
)
и быстро приближается к своему
асимптотическому значению 0.5, то таблица
её значений (Таблица 4) составлена для
 .
Для больших значений аргумента с большой
точностью можно принять
.
Для больших значений аргумента с большой
точностью можно принять
 .
.
Простейший стационарный (Пуассоновский) поток событий
Пусть
на некоторой прямой расположены точки
так, что в среднем на единицу длины
приходится
 точек. Последнее не следует понимать
так, что на любой единичный отрезок
приходится ровно
точек, но если взять достаточно большой
по длине отрезок
точек. Последнее не следует понимать
так, что на любой единичный отрезок
приходится ровно
точек, но если взять достаточно большой
по длине отрезок
 и разделить число точек
,
оказавшихся в нём, на его длину, то
отношение
и разделить число точек
,
оказавшихся в нём, на его длину, то
отношение
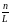 при неограниченном увеличении
при неограниченном увеличении
 будет как угодно мало отличаться от
,
то есть
играет роль средней плотности.
будет как угодно мало отличаться от
,
то есть
играет роль средней плотности.
Вероятность того, что одна точка окажется на отрезке длины l , зависит только от его длины и не зависит от его расположения на прямой. Точки распределяются на прямой независимо друг от друга.
|
|
|
Рис.1.7 |
Определим
теперь вероятность того, что ровно
точек окажется на отрезке длиной
 .
Для этого введём в рассмотрение отрезок
,
целиком включающий в себя отрезок
,
причём,
(Рис.1.7). Согласно принятым допущениям
на отрезке
расположено
.
Для этого введём в рассмотрение отрезок
,
целиком включающий в себя отрезок
,
причём,
(Рис.1.7). Согласно принятым допущениям
на отрезке
расположено
 точек, причём каждая из них может
оказаться в любом месте отрезка
и все эти положения равно возможны.
Вероятность того, что одна из этих точек
окажется на отрезке
,
согласно справедливой в этом случае
геометрической схеме, равна
точек, причём каждая из них может
оказаться в любом месте отрезка
и все эти положения равно возможны.
Вероятность того, что одна из этих точек
окажется на отрезке
,
согласно справедливой в этом случае
геометрической схеме, равна
 и не зависит от того, какая из этих точек
первая, вторая и т.д.
и не зависит от того, какая из этих точек
первая, вторая и т.д.
В
результате мы пришли к схеме Бернулли
(производится
испытаний,
в каждом из которых мы следим за одной
точкой, и любая из них с вероятностью
может оказаться на отрезке
).
Поэтому вероятность того, что ровно
точек из
 окажется на отрезке
,
определяется по формуле Бернулли
окажется на отрезке
,
определяется по формуле Бернулли
 где
;
.
При неограниченном увеличении
,
длина отрезка стремится к бесконечности,
а
к нулю, но при этом величина
где
;
.
При неограниченном увеличении
,
длина отрезка стремится к бесконечности,
а
к нулю, но при этом величина
 остаётся постоянной. Следовательно,
можно применять формулу Пуассона,
которая в данном случае является точной,
а не асимптотической:
остаётся постоянной. Следовательно,
можно применять формулу Пуассона,
которая в данном случае является точной,
а не асимптотической:
 (1.22)
(1.22)
Если
нас интересует вероятность того, что
на отрезке
окажется не менее
 точек, то применяется формула
точек, то применяется формула
 (1.23)
(1.23)
Разумеется,
вместо отрезка на прямой можно
рассматривать плоскость и некоторую
её область, трёхмерный случай или вообще
случай любого числа измерений, а также
временной отрезок. В каждом из этих
случаев
 –
среднее число элементов, приходящихся
на рассматриваемую область.
–
среднее число элементов, приходящихся
на рассматриваемую область.
Формула Пуассона
Рассмотрим
ситуацию, в которой число испытаний
в схеме Бернулли неограниченно
увеличивается, а вероятность наступления
события
в каждом испытании стремится к нулю
таким образом, что произведение
 остаётся величиной постоянной, которую
обозначим
остаётся величиной постоянной, которую
обозначим
 .
В этом случае имеет место соотношение:
.
В этом случае имеет место соотношение:
 (1.19)
(1.19)
Доказательство. По формуле Бернулли

Воспользуемся
тем, что по условию
или
 и
и
 Формула Бернулли принимает вид:
Формула Бернулли принимает вид:

Так
как
и
фиксированы, а
стремится к бесконечности, то множители
 ;
… ;
;
… ;
 и
и
 стремятся к единице, а множитель
стремятся к единице, а множитель
 стремится к
стремится к
 ,
то
,
то

Полученное
выражение называется Пуассоновским
приближением формулы Бернулли. Эта
формула даёт хорошее приближение при
достаточно большом
и малом
(например,
 и
и
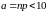 ).
).
Вероятность события, заключающегося в том, что появится не более раз, очевидно, вычисляется по формуле
 (1.20)
(1.20)