14. Разложение в тригонометрический ряд Фурье функции, заданной на интервале [-π: π]. Вид ряда, формулы для коэффициентов с выводом одной из них.

Тригонометрическим рядом Фурье функции f на интервале [-π: π] называется ряд вида:

_*

В тех случаях, когда нужно знать амплитуду n-й гармоники удобна запись ряда в таком виде:

Коэффициенты :

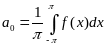
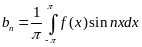
Выведем формулу для коэффициента а₀

Интегрируя в пределах от –π до π обе части разложения (*), получим

Интегралы от остальных членов ряда обратятся в ноль в силу формул:

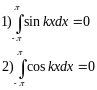
Для любого k

Если k≠0

15. Достаточное условие сходимости ряда Фурье на интервале -π: π] к порождающей функции (теорема Дирихле, формулировка). Сходимость ряда Фурье на всей числовой прямой, нахождение суммы ряда на всей числовой прямой.

Говорят, что функция f(x) периода 2π удовлетворяет условию Дирихле, если на отрезке [0,2π] можно указать конечное число точек 0=x₀<x₁<x₂<…<x_n=2π таких, что на интервалах (x_j,, x_j+1) функция ограничена, непрерывна и монотонна (не убывает или не возрастает), а в точках x_j разрыва f(x)

X₀ – точка разрыва первого рода

т. е. значение f(x) в x_j есть среднее арифметическое правого и левого пределов f(x) в x.

В обеих граничных точках интервала сумма ряда равна среднему арифметическому предельных значений функции при стремлении независимой переменной к этим точкам изнутри интервала

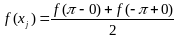
Условия теоремы могут быть несколько иными: можно требовать, чтобы функция f(x) имела в интервале (-π,π) лишь конечное число максимумов и минимумов и была непрерывной, за исключением может быть конечного числа точек разрыва первого рода (условия Дирихле).

16. Ряд Фурье для чётных и нечётных функций: вид ряда, формулы для коэффициентов ( с обоснованием).

Чётная функция

Где

Т.к. f(x)cosnx – чётная функция.

Нечётная функция.

Т.к. f(x)sinnx – чётная функция.

17. Разложение в ряд Фурье функции, заданной на произвольном интервале, вид ряда, формулы для коэффициентов, сходимость к порождающей функции.

Где

Чтобы функция f(x) сходилась к порождающей функции нужно, чтобы функция f(x) имела в интервале (-l,l) лишь конечное число максимумов и минимумов и была непрерывной, за исключением может быть конечного числа точек разрыва первого рода (условия Дирихле).

18. Разложение в ряд Фурье функции, заданной на полуинтервале. Разложение функции в ряд Фурье на полуинтервале по косинусам или по синусам. Исследование сходимости полученного ряда к порождающей функции, нахождение суммы ряда на полном интервале.

Пусть требуется разложить в тригонометрический ряд функцию f(x)в интервале (0,l). Мы можем по произволу продолжить функцию f(x) на интервал (-l,0), но так, чтобы образовавшаяся в этом интервале функция F(x), совпадающая с f(x) в интервале (0,π), удовлетворяла условиям основной теоремы.

График функции можно продолжить чётно (по косинусам), т.е. симметрично относительно оси Оу, или нечётно (по синусам), относительно начала координат.

Сумма ряда находится так же, как и во всех рядах.

19. Случайные события. Классификация событий по возможности их появления: достоверное, невозможное, совместные и несовместные события.

Стохастическим называется эксперимент (опыт, испытание) результат которого заранее (до его проведения) предугадать нельзя.

Случайным событием называется любое явление, которое может произойти или не произойти в результате стохастического эксперимента.

Событие называется достоверным ( ), если оно наступает в результате появления любого элементарного события.

Событие называется невозможным , если оно не наступает ни при каком элементарном событии.

Два события называются несовместными, если их одновременное появление в опыте не возможно. В этом случае .

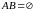Суммой (объединением) двух событий А и В называется событие А + В или , происходящее тогда и только тогда, когда происходит или А, или В.

Сумме событий 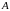и соответствует объединение множеств и .

Отметим очевидные соотношения:

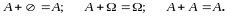
Произведением (пересечением) двух событий А и В называется событие АВ или 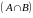, происходящее тогда и только тогда, когда происходит и А , и В.

Произведению событий и соответствует пересечение множеств и .

Отметим очевидные соотношения:

Разностью событий и назовём событие 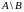, происходящее тогда и только тогда, когда происходит , но не происходит .

Отметим очевидные соотношения:

Событие называется противоположным к А, если оно происходит тогда и только тогда, когда не происходит А.

_{Справедливы следующие свойства:}