10. Расчет математического ожидания и дисперсии ущерба и возмещения и их роль в актуарных расчетах.

A – страховой случай, X – ущерб страхователя, Y – возмещение страховщика. P(A)=p

Математическое ожидание ущерба страхователя:

M(X)=P(A)*M(X|A)+P(Ā)*M(X| Ā)=p*M(X|A).

Условное м.о. ущерба страхователя при наступлении страхового случая:

Дискретное распределение:

Непрерывное распределение:

Y=g(x) – величина возмещения (ущерб страховщика), определяемая условиями договора.

Условное м.о. возмещения страховщика

Условная дисперсия:

Для перехода к безусловному распределению:

M(Y) = P(A)*M(Y|A)=p*M(Y|A)

Математическое ожидание необходимо для оценки возможной величины ущерба, которую придется возмещать по страховым случаям и, соответственно, для оценки рисковой премии. Дисперсию надо знать, чтобы прикинуть какой примерно ожидается разброс ущерба и с этим оценить необходимый объём резервов, рисковую надбавку или возможность перестрахования.

11. Структура страхового тарифа. Чем отличаются: рисковая премия, нетто – премия, брутто – премия? Роль основных составляющих в этой структуре

Брутто-премия – денежная сумма, которую страхователь обязан уплатить страховщику за страховую защиту передаваемого объекта страхования от характерных рисков. БП состоит из нетто-премии (чистой премии) и нагрузки на ведение дела и прибыль (f). Нетто-премия определяется исключительно характеристиками взятого на страхование риска и предназначена для возмещения убытков. Сумма всех НП составляет страховой фонд и идёт на формирование страховых резервов. НП всегда остаётся в групповой собственности страхователей. В страховании жизни НП считают по таблицам смертности или функциям дожития. В рисковых видах – оценка риска как случайной величины. НП делится на 2 части – рисковая премия и рисковая надбавка. Рисковая премия – основная составляющая НП, которая согласно закону больших чисел определяется как мат. ожидание убытка в 1 договоре страхования и отражает основной принцип актуарных расчетов – принцип эквивалентности обязательств сторон, который выражается в равенстве мат. ожиданий 2 величин – суммы всех собранных взносов и суммы всех страховых возмещений.

12. Структура страхового тарифа. Рисковая надбавка. Основные подходы к ее расчету. Квантильный принцип. Деление рисковой надбавки между субпортфелями.

БП = НП + f; НП = РП+РН. Рисковая надбавка – часть НП, необходимая для того, чтобы обеспечить безубыточность страховых операций, если фактическая сумма выплат будет выше мат. ожидания ущерба. Необходимость её формирования обусловлена тем, что страховые портфели на практике всегда ограничены по объёму и остаются зависимыми от случайности. РН также называют гарантийной, так как она обеспечивает надёжность и гарантирует повышение финансовой устойчивости страховой компании. Имеется большое число методов расчёта РН, как правило, связанных с характеристиками разброса возможного ущерба по договору страхования. Самый простой и распространенный – квантильный принцип или метод доверительного оценивания. Согласно этому методу задается вероятность неразорения страховой компании (1-ε) и для заданного уровня надёжности γ=1-2ε строится доверительный интервал для совокупного ущерба по всему портфелю и разница между правой границей этого доверительного интервала и математическим ожиданием совокупного ущерба составляет рисковую надбавку.

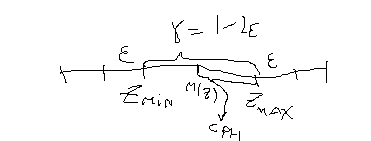Z – совокупный убыток по всему портфелю.

Согласно центральной предельной теореме:

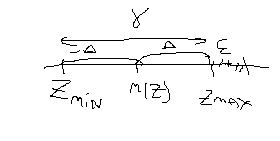
При увеличении портфеля договоров в n раз РН на 1 договор уменьшится согласно квантильному принципу в раз. Именно поэтому страховые компании, собирающие большие портфели договоров могут предложить своим клиентам более низкие тарифы, повысив свою конкурентоспособность, при этом сохранив уровень финансовой надежности.

Деление рисковой надбавки:

1. Независимые риски (r=0) – РН делится между субпортфелями пропорционально доли дисперсии субпортфеля в общей дисперсии портфеля.

2. Зависимые риски (например, в страховании кредитов (зависят от конъюнктуры рынка), от стихийных бедствий (от географического положения)). РН необходимо делить пропорционально доле СКО субпортфеля в общем СКО.

Общее правило деления для РН: При разложении совокупного портфеля Y на любые не обязательно независимые части совокупная РН делится так, чтобы на части Y_i приходилась доля РН равная отношению соответствующей ковариации к общей дисперсии.