Результаты проведенного анализа:

Нормальный режим

Критическое время завершения строительства: 40 дней

Критический путь:

L_кр.1={V;Q;H;A;D}

L_кр.2={V;Q;H;F}

L_кр.3={V;Q;B;D}

Суммарная стоимость: 556,8 тыс. руб.

Директивный срок

Критическое время завершения строительства: 38 дней

Критические пути:

L_кр.1={V;Q;H;A;D

L_кр.2={V;Q;H;F}

L_кр.3={V;Q;B;D}

L_кр.4={G;H;A;D}

L_кр.5={G;H;F} L_кр.6={G;B;D}

Суммарная стоимость: 576,2 тыс. руб.

Задача №6

1. Построим поля рассеяния для зависимости y(x):

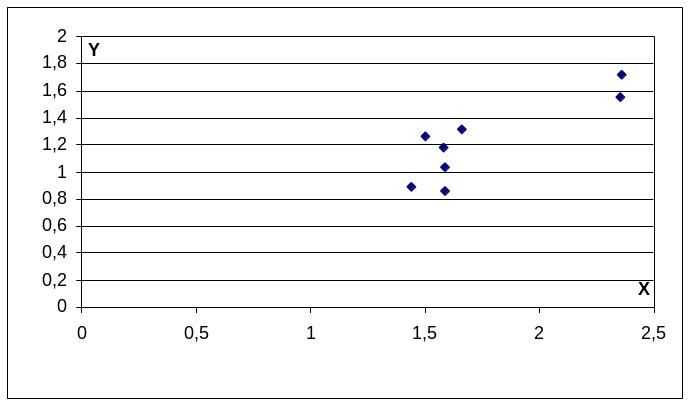
На основе анализа диаграммы выдвигаем гипотезу о том, что зависимость между денежными доходами и потребительскими расходами линейная. Эту зависимость можно описать в виде математической модели: , где

₀, ₁ – параметры модели;

 - некоторая ошибка, благодаря которой любое индивидуальное значение y может отклоняться от линии регрессии.

2. Используя метод наименьших квадратов, найдем точечные оценки параметров модели. Для этого составим вспомогательную расчетную таблицу

№	X	Y	X2	Y2	XY
1	1,66	1,32	2,7556	1,7424	2,1912
2	1,59	0,86	2,5281	0,7396	1,3674
3	1,59	1,04	2,5281	1,0816	1,6536
4	1,58	1,18	2,4964	1,3924	1,8644
5	2,36	1,72	5,5696	2,9584	4,0592
6	2,35	1,55	5,5225	2,4025	3,6425
7	1,44	0,89	2,0736	0,7921	1,2816
8	1,5	1,26	2,25	1,5876	1,89
	14,07	9,82	25,7239	12,6966	17,9499

Для нахождения параметров уравнения регрессии составляется система линейных уравнений

,

Коэффициенты этой системы находятся по формулам:

, , ,

,

,

y=0,007+0,694x

Построим прямую регрессии на графике

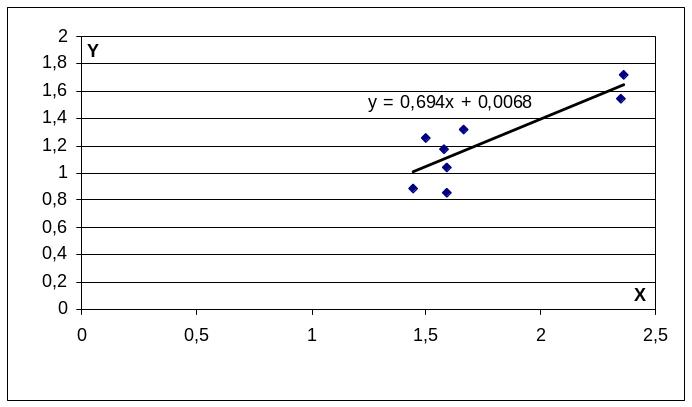
3. Найдем коэффициент парной корреляции между X и Y.

Положительное значение коэффициента корреляции говорит о том, что связь прямая, а его значение – о том, что связь высокая.

Проверим значимость r_xy при уровне значимости =0,1. По таблице находим:

t_кр(1- ;n-2)=t_кр(0,95;6)=1,943.

Рассчитаем t-статистику:

Т.к. >t_кр(1- ;n-2), то коэффициент корреляции статистически значим.

Определим коэффициент детерминации R². В случае парной регрессии

R²= =0,856²=0,733

4. Найдем точечный прогноз среднемесячных потребительских расходов в 8-м субъекте.

x₈=1,51,3=1,95 тыс. руб. 

y₈=0,007+0,6941,95=1,36 тыс. руб.

Найдем интервальный прогноз среднемесячных потребительских расходов в 8-м субъекте по формуле:

, где

y_в, y_н – верхняя и нижняя граница доверительного интервала

- значение независимой переменной x, для которой определяется доверительный интервал

- квантиль распределения Стьюдента с доверительной вероятностью 1- и числом степеней свободы n-2. При =0,1 t_0,95;6=1,943.

Значение S_y определяется по формуле:

,

Для промежуточных расчетов составим таблицу:

№	X	Y
1	1,66	1,32	1,159	0,026	0,010
2	1,59	0,86	1,110	0,063	0,028
3	1,59	1,04	1,110	0,005	0,028
4	1,58	1,18	1,103	0,006	0,032
5	2,36	1,72	1,645	0,006	0,362
6	2,35	1,55	1,638	0,008	0,350
7	1,44	0,89	1,006	0,014	0,102
8	1,5	1,26	1,048	0,045	0,067
Итого	14,07	9,82	9,820	0,171	0,978

Тогда:

,

y_н=1,36-1,9430,068=1,473

y_в=1,36+1,9430,068=2,067

y[1,228;1,493]

Т.е. с вероятностью 90% можно утверждать, что потребительские расходы будут находиться в интервале от 1,228 до 1,493 тыс. руб.

5. Проведем содержательную интерпретацию полученных результатов.

Найденная прямая регрессии, изображенная на рисунке вместе с полем рассеяния, наилучшим образом приближается к заданным точкам. Найденный коэффициент корреляции r_xy=0,856 свидетельствует о высокой и прямой линейной связи между денежными доходами и потребительскими расходами на душу населения.

Из найденного уравнения регрессии можно сказать, что при росте доходов на душу населения на 1 тыс. руб. потребительские расходы увеличатся в среднем по 8 субъектам РФ на 694 руб.

Чтобы заключение о тесноте линейной зависимости было обоснованным, была доказана значимость коэффициента корреляции.

Величина коэффициента детерминации R²=0,733 показывает, что 73,3% дисперсии признака y объясняется построенным уравнением регрессии.

В 4-м пункте был найден точечный прогноз потребительских расходов при заданном среднегодовом доходе, но так как вероятность совпадения фактического значения с точечным прогнозом равна 0, то был построен доверительный интервал, в который с 90%-ой вероятностью попадет фактическое значение y.

y=0,007+0,694x

y₈=1,36 тыс. руб.

y[1,228;1,493]