Задача №4

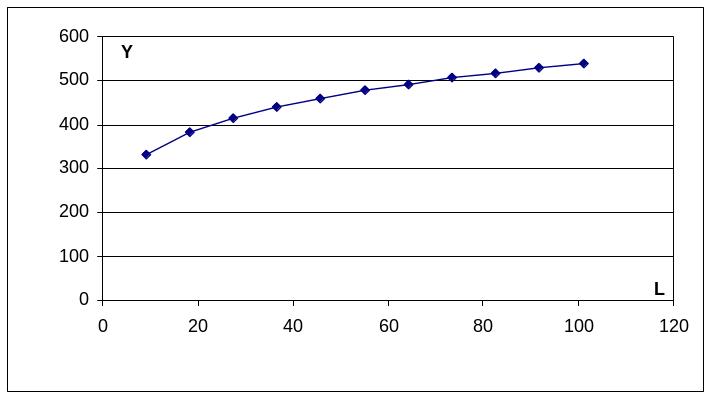
1. Фиксируем значение K=72, тогда

Y(L;72)=7L^0,272^0,8

Построим график при изменении рабочей силы в пределах 10≤L≤100

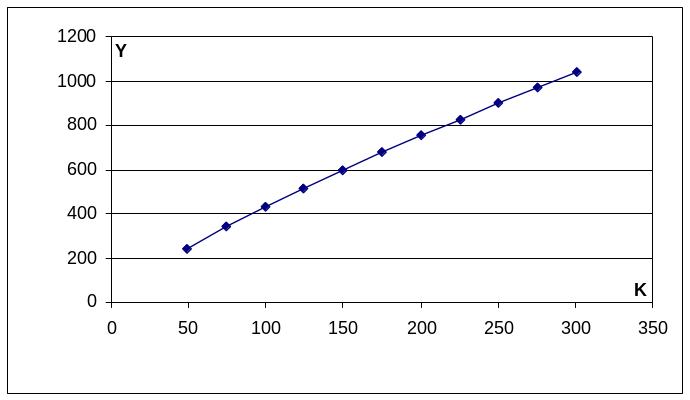
Фиксируем значение L=9, тогда

Y(9;K)=79^0,2K^0,8

Построим график при изменении оборудования в пределах 50≤K≤300

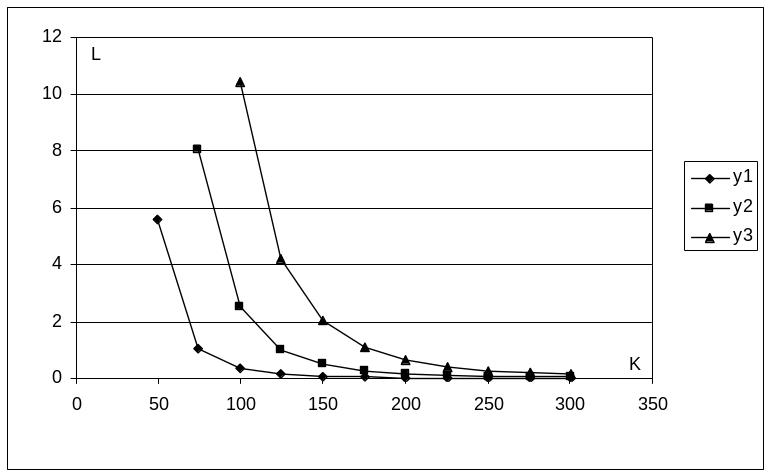
2. Изоквантой производственной функции называется совокупность всех точек K и L, при которых производственная функция принимает одно и то же значение.

Составим уравнения изоквант при фиксированных значениях объема выпуска продукции:

y₁=222: 7L^0,2K^0,8=222 (1 изокванта)

y₂=333: 7L^0,2K^0,8=333 (2 изокванта)

y₃=445: 7L^0,2K^0,8=445 (3 изокванта)

Построим их графики:

3.

y_баз=333

L_баз=9

y_пл=1,1y_баз=1,1333=366,3

L_пл=1,05L_баз=1,059=9,45

Используя уравнение изокванты Y=7L^0,2K^0,8=366,3, получим выражение для потребности в оборудовании:

Если объем трудовых ресурсов не изменится, то потребность в оборудовании в базовом периоде составит

(тыс. ст.-час.)

Если объем трудовых ресурсов увеличится на 5%, то потребность в оборудовании в плановом периоде составит

(тыс. ст.-час.)

4. Составим ограничение по величине денежных средств, которые фирма может затратить на приобретение ресурсов:

p_LL+p_KK≤C

40L+20K≤2000

Тогда экономико-математическая модель задачи будет иметь вид:

Y(L,K)=7L^0,2K^0,8max

Т.е. нужно найти точку касания самой высокой изокванты с линией бюджетного ограничения.

Y(L,K)=7L^0,2K^0,8max

40L+20K=2000

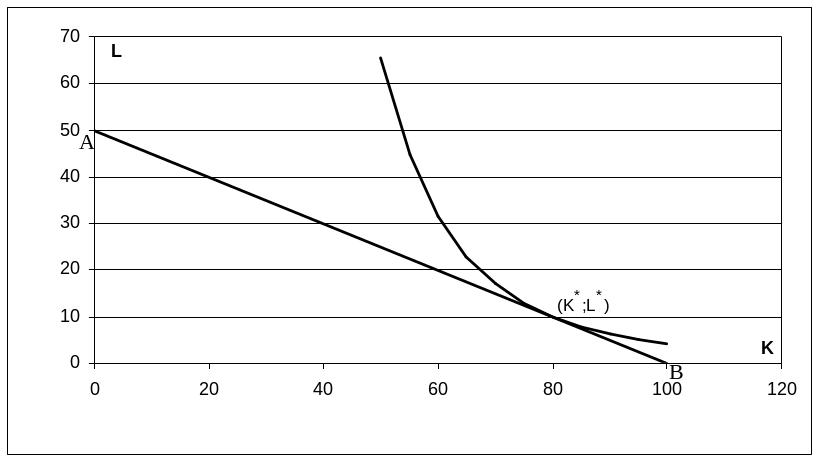
Граничная прямая АВ бюджетного ограничения задается уравнением: 40L+20K=2000.

Для нахождения оптимального решения используем тот факт, что градиент целевой функции в точке касания будет перпендикулярен прямой АВ. Поэтому имеем равенство:

=5,6L^0,2K^-0,2, а =1,4L^-0,8K^0,8, то  L= K

Подставим это выражение в бюджетное ограничение:

40 K+20K=2000  25K=2000  K^*=80, тогда L^*= 80=10

При этом объем выпуска продукции максимален и составляет:

Y(L;K)=710^0,280^0,8=369,46 ед.

Определим предельную норму технологического замещения оборудования рабочей силой:

Эта величина показывает, что затраты рабочей силы нужно увеличить на 0,5 единиц, чтобы при уменьшении затрат оборудования на одну единицу объем выпуска продукции остался на прежнем уровне.

Определим предельную эффективность финансовых ресурсов:

Эта величина показывает, что при увеличении объема капитала на 1 денежную единицу производительность увеличится на 0,1847 единиц.

Задача №5

С учетом технологической последовательности работ построим сетевой график выполнения этих работ:

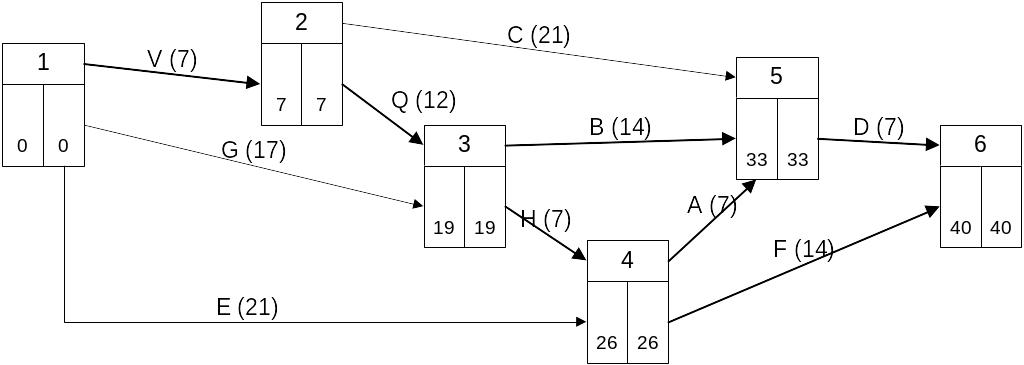
Прямоугольниками на сетевом графике обозначены события; в прямоугольниках сверху записан номер события, в левой части прямоугольника находится раннее, а в правой части – позднее время выполнения работ. Стрелками обозначены работы. Жирными стрелками обозначены работы, принадлежащие критическому пути. Над стрелочками написано имя работы, а в скобках - нормальный срок выполнения работы,

2. Рассчитаем временные характеристики сетевого графика при нормальном режиме выполнения работ. Найдем критический путь и его продолжительность, укажем все возможные критические пути и определим стоимость всего комплекса работ.

Рассчитаем раннее время выполнения работ:

Т_р1=0 дн.

Т_р2=Т_р1+t₁₂=0+7=7 дн.

Т_р3=max[Т_р1+t₁₃;Т_р2+t₂₃]=max[0+17;7+12]=19 дн.

Т_р4=max[Т_р1+t₁₄;Т_р3+t₃₄]=max[0+21;19+7]=26 дн.

Т_р5=max[Т_р2+t₂₅;Т_р3+t₃₅;Т_р4+t₄₅]=max[7+21;19+14;26+7]=33 дн.

Т_р6=max[Т_р4+t₄₆;Т_р5+t₅₆]=max[26+14;33+7]=40 дн.

Итак, раннее время конечного события графика равно Т_р(кр.)=Т_р6=40 дней, т.е. раньше чем через 40 дней строительство торгового павильона завершено быть не может.

Обратным ходом находим критические пути L_кр.:

L_кр.1={V;Q;H;A;D} L_кр.2={V;Q;H;F} L_кр.3={V;Q;B;D}

Определим стоимость строительства торгового павильона при нормальном режиме выполнения работ:

S_норм.=1,8+91,2+16,2+49,2+9+105,6+109,2+56,4+58,2+60=556,8 тыс. руб.

Рассчитаем позднее время выполнения работ:

Т_п6=Т_р6=40 дн.

Т_п5=Т_п6-t₅₆=40-7=33 дн.

Т_п4=min[Т_п5-t₄₅;Т_п6-t₄₆]=min[33-7;40-14]=26 дн.

Т_п3=min[Т_п4-t₃₄;Т_п5-t₃₅]=min[26-7;33-14]=19 дн.

Т_п2=min[Т_п3-t₂₃;Т_п5-t₂₅]=min[19-12;33-21]=7 дн.

Т_п1=Т_р1=0 дн.

3. Укажем стратегию минимального удорожания комплекса работ при сокращении сроков строительства на 2 дня, и в какую итоговую сумму обойдётся фирме ускоренная стройка павильона:

Рассчитаем затраты на ускорение строительства и предельно-возможное уменьшение длительности в днях в таблице:

Работа	A	B	C	D	E	F	G	H	Q	V
tнорм.-tср	1	2	3	1	3	2	5	1	6	1
,(тыс.руб.)	0,3	7,6	0,9	8,2	0,5	8,8	9,1	9,4	9,7	10

где  = норма платы за ускорение за каждый день.

Критический срок будем сокращать последовательно по одному дню за счёт ускорения критических работ. В данном случае это будет работа Q.

Шаг первый:

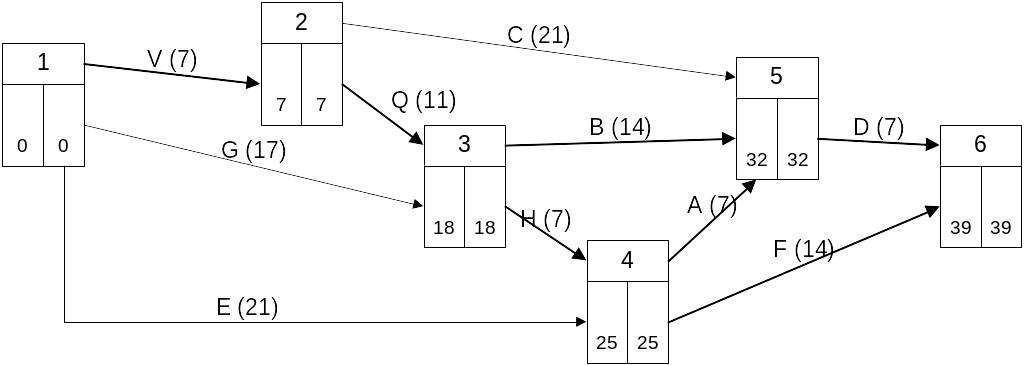
Результаты ускорения:

Ускоряемая работа: Q

Новая длительность: 11 дней

Критические пути со временем завершения работ за 39 дней

L_кр.1={V;Q;H;A;D} L_кр.2={V;Q;H;F} L_кр.3={V;Q;B;D}

Суммарная стоимость: 566,5 тыс. руб.

Шаг второй:

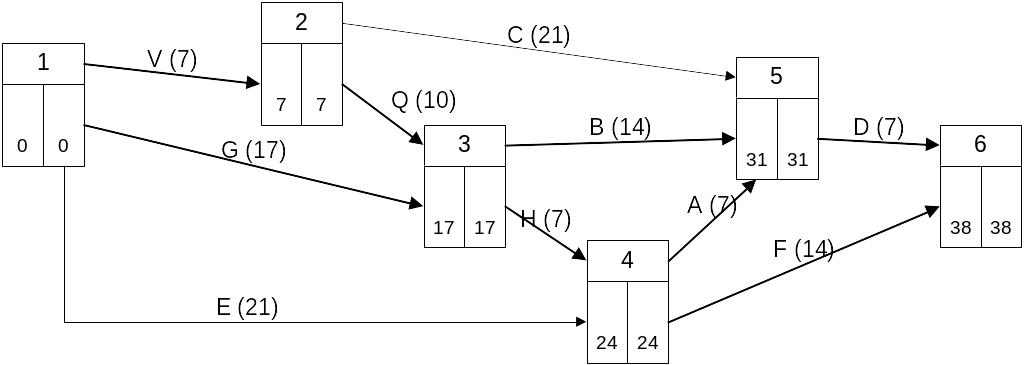
Результаты ускорения:

Ускоряемая работа: Q

Новая длительность: 10 дней

Критические пути со временем завершения работ за 38 дней

L_кр.1={V;Q;H;A;D} L_кр.2={V;Q;H;F} L_кр.3={V;Q;B;D}

L_кр.4={G;H;A;D} L_кр.5={G;H;F} L_кр.6={G;B;D}

Суммарная стоимость: 576,2 тыс. руб.