Оглавление

Задача №1……………………………….....................................................................3

Задача №2…………………………………………………………………………….7

Задача №3…………………………………………………………………………….9

Задача №4…………………………………………………………………………...15

Задача №5…………………………………………………………………………...20

Задача №6…………………………………………………………………………...23

Библиографический список

Задача №1

1. Построим математическую модель оптимизации выпуска продукции и запишем ее в форме задачи линейного программирования:

Обозначим:

x₁ – количество производимой продукции А

x₂ – количество производимой продукции Б

Тогда производственная программа выпуска изделий А и Б будет определяться вектором X=(x₁;x₂)

Искомая программа должна удовлетворять всем ресурсным ограничениям:

4x₁+x₂209

x₁+2x₂117

8x₁+x₂635

Z=244x₁+166x₂MAX

2. Используя графический метод решения задачи линейного программирования, найдем оптимальную программу выпуска продукции:

I. 4x₁+x₂=209

x1	0	52,25
x2	209	0

II. x₁+2x₂=117

x1	0	117
x2	58,5	0

III. 8x₁+x₂=635

x1	0	79,4
x2	635	0

Так как О.Д.Р. представляет собой некоторый замкнутый многоугольник, полученный путём пересечения полуплоскостей, отвечающих отдельным неравенствам задачи, определим по какую сторону от граничных прямых располагается искомая полуплоскость. Для этого в каждое из трёх неравенств – ограничений подставим пробную точку (0;0):



Т.к. точка (0;0) удовлетворяет всем трём неравенствам, то искомые полуплоскости будут располагаться слева (ниже) граничных прямых (1) –(3).

Кроме основных ограничений на ресурсы, в задаче имеются также тривиальные неравенства Х₁0; Х₂0. Неравенству Х₁0 отвечает полуплоскость, расположенная справа от оси Х₂, а граничная прямая, задаваемая уравнением Х₁=0 совпадает с осью Х₂. Граничная прямая Х₂=0 совпадает с осью Х₁, а множество точек удовлетворяющих неравенству Х₂0 – это полуплоскость, лежащая выше оси ОХ. Изобразим О.Д.Р. графически:

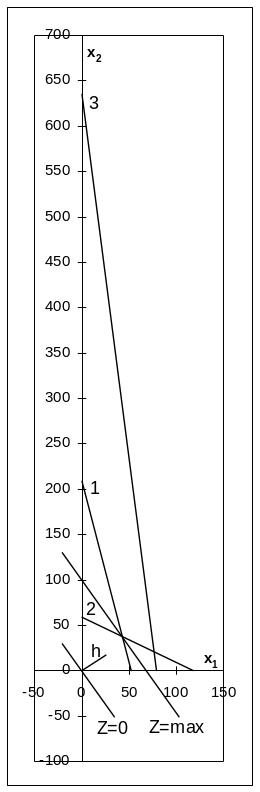
Найдём теперь в этой области точку максимума целевой функции Z: grad Z=(244;166)= . Из начала координат, в направлении вектора откладываем вектор произвольной длины и перпендикулярно ему проведём через начало координат нулевую линию уровня.

Двигая эту линию в направлении вектора или параллельно самой себе, достигнем самой крайней точки О.Д.Р., это и будет точка максимума целевой функции Z:

Х^*=(Х₁^*;Х₂^*). В нашей задаче точка Х^* лежит на пересечении граничных прямых (I) и (II):

Х^*: 

Оптимальная производственная программа Х*=(43;37) состоит в выпуске 43 ед. продукции А и 37 ед. продукции Б.

Ожидаемая выручка от их реализации составит:

Z=24443+16637=16634 руб.

3. Запишем задачу, двойственную к задаче оптимизации выпуска продукции.

Исходная задача:

u₁ 4x₁+x₂209

u₂ x₁+2x₂117

u₃ 8x₁+x₂635

x₁0; x₂0

Z=244x₁+166x₂MAX

Двойственная задача:

x₁ 4u₁+u₂+8u₃244

x₂ u₁+2u₂+u₃166

u₁0; u₂0; u₃0

W=209u₁+117u₂+635u₃MIN

Здесь u₁, u₂, u₃ – двойственные оценки используемых ресурсов.

Используя условия «дополняющей нежесткости», найдём оптимальное решение двойственной задачи:

Условия «дополняющей нежесткости»:

1: Х_jV_j=0;

2: U_iY_i=0;

При известном оптимальном векторе Х^*=(43;37):

1: X₁V₁=0  X₁=43  V₁=0 ~ 4u₁+u₂+8u₃=244

X₂V₂=0  X₂=37  V₂=0 ~ u₁+2u₂+u₃=166

2: U₁Y₁=0  Y₁=209-4X₁-X₂=209-443-37=0,  U₁0

U₂Y₂=0  Y₂=117-X₁-2X₂=117-43-237=0  U₂0

U₃Y₃=0  Y₃=635-8X₁-X₂=635-843-37=254,  U₃=0

Итак, получили систему уравнений:

  U^*=(46;60;0)

Оптимальные целевой функции при этом

W^*=20946+11760+6350=16634 руб.

Получены следующие результаты расчета модели:

X^*=(43;37)

U^*=(46;60;0)

Z^*=W^*=16634 руб.

Проведем экономическую интерпретацию полученных результатов решения двойственной задачи:

Единицы измерения двойственных оценок определяются по формуле: (U_i)=(Z)/(b_i),

где (U_i); (Z); (b_i) - единицы измерения соответственно двойственной оценки оптимизируемого показателя и ресурса i-ого вида.

В нашей задаче оптимизируемый показатель – выручка Z, измеряемая в рублях, единицы измерения ресурсов заданы в исходных данных задачи.

Итак: (U₁)= руб./кг.; (U₂)= руб./ст.-час; (U₃)= руб./чел.-час.

Оптимальная оценка U₁=46 руб./кг означает, что если имеющийся объем сырья увеличить (снизить) на 1 кг, то ожидаемая выручка может увеличиться (снизиться) на 46 руб.

Оптимальная оценка ресурса оборудования U₂=60 руб./ст.-час показывает, что если имеющийся фонд времени на оборудование увеличить (снизить) на 1 кг, то ожидаемая выручка может увеличиться (снизиться) на 60 руб.

Оптимальная оценка U₃=0 руб./чел.-час означает, что объем трудоресурса в данном объеме является избыточным, т.е. он недоиспользуется.