
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
"Кузбасский государственный технический университет"
Кафедра информационных и автоматизированных
производственных систем
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ И ИНЖЕНЕРНАЯ ГРАФИКА
Методические указания к выполнению расчетно-графической работы для студентов специальностей 210200
очной формы обучения
Составитель ПУДОВ Е.Ю.
Утверждены на заседании кафедры
Протокол № 4 от 25.01.07
Рекомендованы к печати
учебно-методической комиссией
специальности 210200
Протокол № от
Электронная копия находится
в библиотеке главного корпуса
ГУ КузГТУ
Прокопьевск 20??
1.Цель работы
Целью выполнения расчетно-графической работы является закрепление полученных знаний по курсу начертательной геометрии.
Данные методические указания содержат в себе варианты заданий, а так же краткое описание по их выполнению.
2.Теоретические положения
2.1.Условные обозначения
Прежде чем приступить к выполнению заданий, следует повторить основные условные обозначения, используемые в данной работе:
1. Плоскости проекций:
П1 – горизонтальная,
П2 – фронтальная,
П3 – профильная.
2. Оси проекций – x, y, z.
3. Точки – А, В или 1, 2, 3.
4. Прямые – a, b, c и т.д.
5. Отрезки прямых – AB, CD, EF…
6. Линии уровня:
h – горизонталь,
f – фронталь,
p – профильная прямая уровня
7. Плоскости – P, Q, S …
8. Следы плоскостей:
PП1, QП1, SП1 – горизонтальные следы плоскостей и т.д.
3. Рекомендации по выполнению работы
Работу следует выполнять на на листах стандартного формата А4 или А3 по ГОСТ 2.301-68 – «Форматы» (в зависимости от необходимости и масштаба построений. Каждое задание оформляется на отдельном листе с расчерченными полями и основной надписью, как показано на рисунке 1:
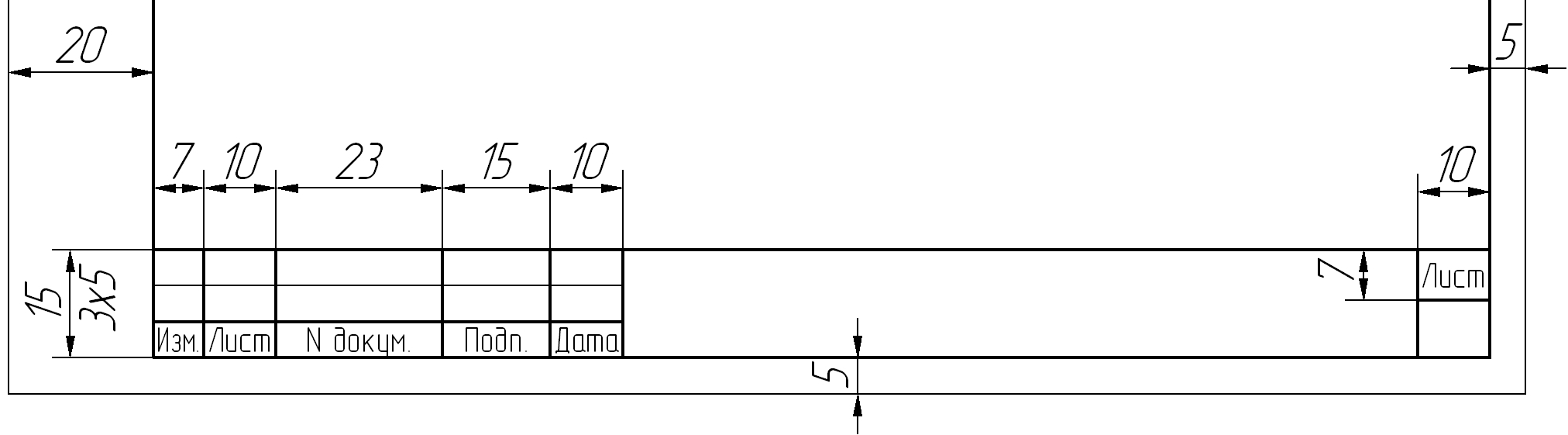
Рисунок 1 – Основная надпись
Все задания выполнить с помощью чертежных инструментов остро заточенным карандашом. Изображения на поле чертежа располагать равномерно.
Все листы расчетно-графической работы необходимо сброшюровать с титульным листом, пример заполнения которого приведен в приложении 1.
4. ВАРИАНТЫ ЗАДАНИЙ И ПРИМЕРЫ ВЫПОЛНЕНИЯ
1. По заданным в таблице 1 координатам построить наглядное изображение точек A,B,C, и D, и эпюры этих точек. Построение точек произвести на одном чертеже, как для эпюра, так и для наглядного изображения.
При построении наглядного изображения ось ОY проводится из точки О под углом 45 градусов к горизонтали; по оси ОY откладывается половина заданного в таблице размера, по осям ОХ и ОZ – натуральная величина. При построении ортоганальных проекций точки по заданным координатам размеры откладываются по всем осям в натуральную величину.
Таблица 1
№ варианта |
A |
B |
C |
D |
||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
1 |
10 |
20 |
30 |
0 |
20 |
30 |
25 |
0 |
15 |
20 |
40 |
0 |
2 |
30 |
20 |
15 |
20 |
30 |
0 |
0 |
30 |
40 |
40 |
0 |
35 |
3 |
15 |
30 |
40 |
30 |
0 |
20 |
30 |
20 |
0 |
0 |
30 |
15 |
4 |
40 |
30 |
20 |
0 |
30 |
40 |
20 |
0 |
35 |
15 |
20 |
0 |
5 |
35 |
40 |
15 |
40 |
0 |
20 |
0 |
40 |
20 |
40 |
20 |
0 |
6 |
20 |
30 |
15 |
30 |
40 |
0 |
15 |
0 |
35 |
0 |
40 |
30 |
7 |
35 |
20 |
10 |
0 |
25 |
40 |
10 |
40 |
0 |
25 |
0 |
30 |
8 |
30 |
40 |
15 |
35 |
0 |
15 |
0 |
20 |
30 |
35 |
20 |
0 |
9 |
45 |
30 |
30 |
15 |
30 |
0 |
15 |
0 |
20 |
0 |
40 |
20 |
10 |
20 |
40 |
30 |
0 |
40 |
30 |
40 |
30 |
0 |
10 |
0 |
30 |
11 |
15 |
20 |
30 |
25 |
0 |
30 |
0 |
40 |
15 |
25 |
15 |
0 |
12 |
30 |
30 |
40 |
30 |
15 |
0 |
35 |
0 |
25 |
0 |
30 |
20 |
13 |
25 |
30 |
35 |
0 |
25 |
15 |
15 |
40 |
0 |
20 |
0 |
30 |
14 |
10 |
30 |
40 |
15 |
0 |
30 |
0 |
20 |
10 |
30 |
40 |
0 |
15 |
25 |
20 |
35 |
35 |
40 |
0 |
30 |
0 |
10 |
0 |
40 |
15 |
16 |
35 |
40 |
20 |
0 |
25 |
30 |
25 |
40 |
0 |
35 |
0 |
10 |
17 |
15 |
30 |
15 |
10 |
0 |
40 |
0 |
30 |
15 |
10 |
20 |
0 |
18 |
20 |
10 |
30 |
15 |
20 |
0 |
20 |
0 |
10 |
0 |
25 |
10 |
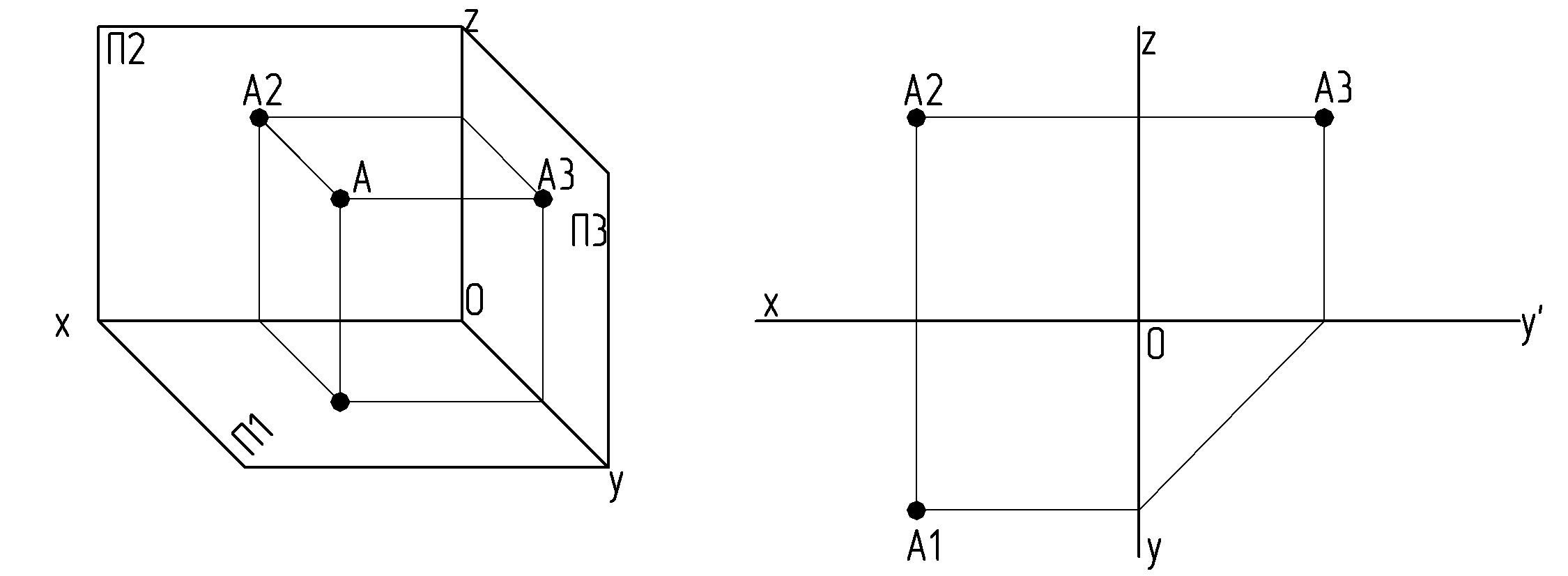
Рисунок 1 – Пример построения точки по координатам
2. По заданным в таблице 2 координатам построить наглядное изображение отрезка прямой AB, CD, MN и эпюр.
При построении наглядного изображения ось ОУ проводится из точки О под углом 45 градусов к горизонтали; по оси ОУ откладывается половина заданного в таблице размера, по осям ОХ и ОZ – натуральная величина. При построении ортоганальных проекций отрезка прямой по заданным координатам размеры откладываются по всем осям в натуральную величину.
Таблица 2
№ варианта |
Прямая 1 |
Прямая 2 |
Прямая 3 |
|||||||||||||||
A |
B |
C |
D |
M |
N |
|||||||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
1 |
35 |
40 |
15 |
15 |
20 |
30 |
0 |
20 |
35 |
40 |
40 |
10 |
0 |
20 |
30 |
40 |
20 |
30 |
2 |
15 |
20 |
35 |
30 |
30 |
15 |
20 |
0 |
40 |
40 |
30 |
15 |
30 |
20 |
0 |
30 |
20 |
45 |
3 |
40 |
20 |
45 |
20 |
40 |
20 |
30 |
40 |
0 |
10 |
20 |
35 |
30 |
0 |
20 |
30 |
40 |
20 |
4 |
50 |
10 |
15 |
20 |
30 |
35 |
0 |
30 |
20 |
30 |
45 |
10 |
20 |
50 |
5 |
20 |
40 |
45 |
5 |
45 |
20 |
5 |
15 |
40 |
25 |
40 |
0 |
10 |
20 |
30 |
40 |
0 |
30 |
5 |
40 |
30 |
5 |
6 |
30 |
40 |
45 |
10 |
40 |
15 |
35 |
20 |
0 |
10 |
40 |
30 |
40 |
0 |
25 |
40 |
30 |
25 |
7 |
40 |
30 |
15 |
15 |
30 |
40 |
0 |
40 |
15 |
35 |
20 |
40 |
15 |
40 |
0 |
15 |
40 |
35 |
8 |
30 |
10 |
40 |
35 |
40 |
20 |
25 |
0 |
35 |
40 |
30 |
20 |
0 |
40 |
35 |
40 |
40 |
35 |
9 |
20 |
40 |
30 |
40 |
20 |
10 |
40 |
30 |
0 |
20 |
40 |
35 |
30 |
20 |
20 |
30 |
50 |
20 |
10 |
50 |
30 |
25 |
15 |
20 |
10 |
0 |
40 |
25 |
40 |
30 |
5 |
25 |
0 |
15 |
25 |
55 |
15 |
11 |
10 |
20 |
40 |
25 |
40 |
10 |
45 |
0 |
10 |
10 |
50 |
40 |
30 |
40 |
0 |
30 |
40 |
35 |
12 |
25 |
10 |
35 |
40 |
20 |
20 |
50 |
40 |
0 |
10 |
10 |
30 |
40 |
20 |
30 |
0 |
20 |
30 |
13 |
15 |
30 |
15 |
30 |
20 |
40 |
0 |
40 |
50 |
45 |
20 |
20 |
50 |
50 |
25 |
50 |
0 |
25 |
14 |
35 |
20 |
10 |
15 |
30 |
40 |
30 |
0 |
10 |
15 |
50 |
35 |
45 |
40 |
35 |
45 |
40 |
0 |
15 |
10 |
40 |
15 |
35 |
20 |
30 |
10 |
50 |
0 |
40 |
10 |
40 |
35 |
20 |
25 |
0 |
20 |
25 |
16 |
15 |
10 |
30 |
30 |
20 |
30 |
0 |
20 |
40 |
45 |
50 |
10 |
15 |
50 |
20 |
15 |
0 |
20 |
17 |
40 |
20 |
15 |
40 |
40 |
30 |
40 |
0 |
20 |
15 |
20 |
45 |
10 |
50 |
40 |
10 |
50 |
0 |
18 |
40 |
10 |
10 |
20 |
20 |
30 |
25 |
40 |
0 |
5 |
30 |
40 |
30 |
10 |
35 |
0 |
10 |
35 |
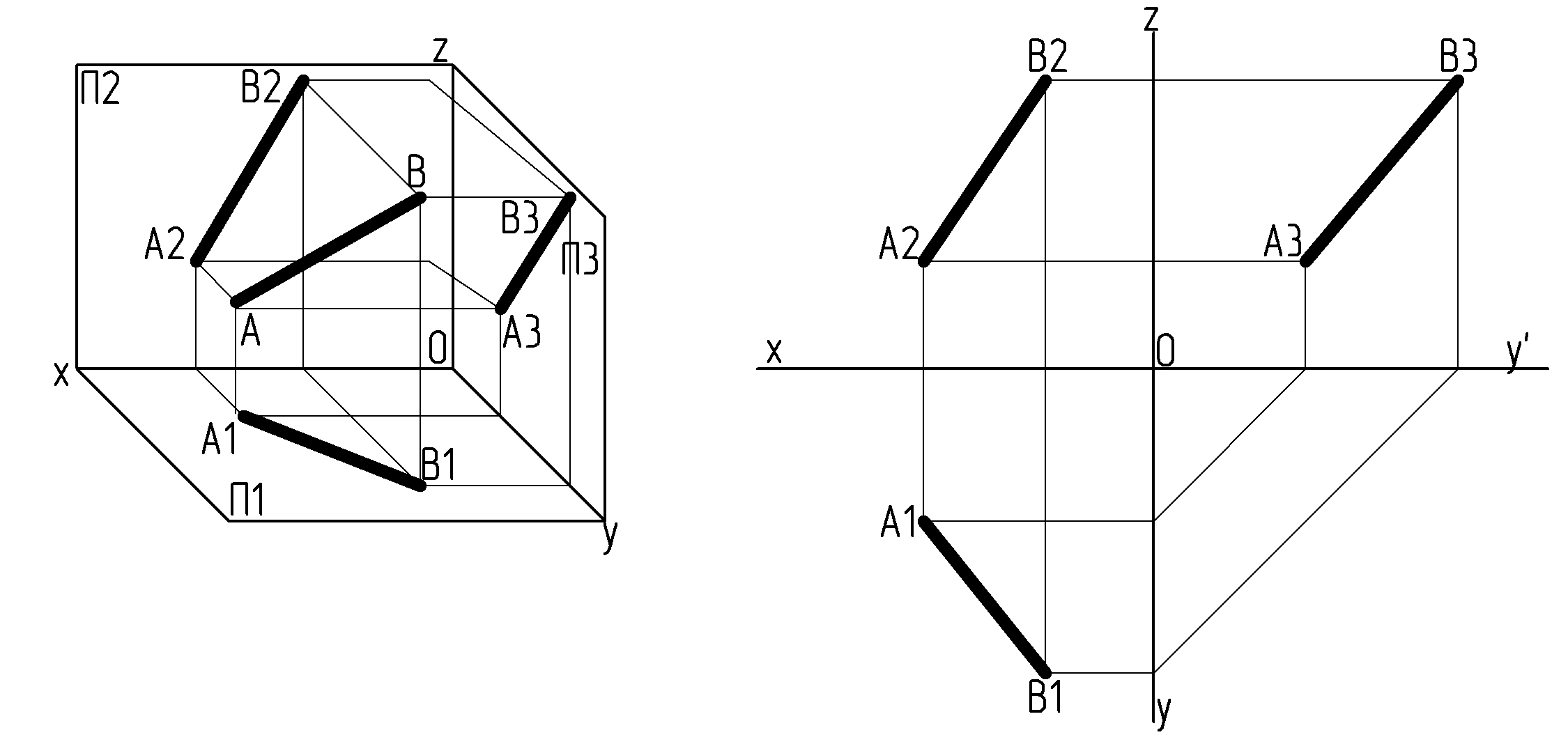
Рисунок 2 – Пример построения прямой
3. Построить ортогональный чертеж плоскости общего положения, заданной параллелограммом с вершинами D,E,F,G. За диагональ параллелограмма принять прямую DF в вариантах 1 – 3, 5 – 6; прямую EF - в варианте 4 и прямую DE - в остальных вариантах.
При построении чертежа координаты 3-х точек (D, E, F), определяющих плоскость, взять из приведенной таблицы 3, а вершину G найти построением как точку, принадлежащую заданной плоскости.
Таблица 3
№ варианта |
A |
B |
C |
D |
E |
F |
||||||||||||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
||||||
1 |
55 |
50 |
50 |
15 |
25 |
0 |
95 |
0 |
15 |
15 |
15 |
35 |
85 |
35 |
0 |
50 |
0 |
35 |
|
|||||
2 |
95 |
0 |
20 |
65 |
55 |
50 |
15 |
40 |
0 |
30 |
25 |
50 |
55 |
45 |
0 |
85 |
0 |
40 |
|
|||||
3 |
110 |
35 |
10 |
45 |
0 |
50 |
20 |
55 |
10 |
95 |
50 |
40 |
50 |
10 |
0 |
15 |
25 |
10 |
|
|||||
4 |
50 |
45 |
35 |
20 |
30 |
20 |
95 |
10 |
0 |
20 |
10 |
0 |
95 |
20 |
0 |
75 |
50 |
0 |
|
|||||
5 |
25 |
50 |
0 |
40 |
10 |
50 |
95 |
35 |
0 |
50 |
0 |
0 |
80 |
50 |
35 |
20 |
15 |
15 |
|
|||||
6 |
85 |
50 |
40 |
15 |
20 |
40 |
110 |
5 |
0 |
100 |
15 |
50 |
70 |
50 |
0 |
40 |
35 |
20 |
|
|||||
7 |
100 |
0 |
0 |
80 |
35 |
40 |
20 |
50 |
35 |
85 |
45 |
0 |
115 |
0 |
30 |
50 |
0 |
30 |
|
|||||
8 |
60 |
5 |
40 |
90 |
55 |
0 |
15 |
15 |
0 |
90 |
10 |
5 |
75 |
0 |
25 |
30 |
45 |
25 |
|
|||||
9 |
10 |
15 |
0 |
80 |
55 |
50 |
90 |
5 |
0 |
55 |
45 |
0 |
100 |
10 |
35 |
70 |
10 |
35 |
|
|||||
10 |
15 |
15 |
20 |
70 |
50 |
50 |
100 |
0 |
0 |
95 |
45 |
0 |
60 |
0 |
45 |
20 |
0 |
45 |
|
|||||
11 |
115 |
20 |
0 |
10 |
55 |
0 |
35 |
5 |
45 |
65 |
15 |
0 |
95 |
55 |
50 |
60 |
45 |
50 |
|
|||||
12 |
90 |
5 |
45 |
10 |
40 |
25 |
75 |
55 |
0 |
95 |
5 |
0 |
60 |
5 |
0 |
20 |
55 |
45 |
|
|||||
13 |
105 |
35 |
15 |
70 |
50 |
55 |
30 |
5 |
15 |
70 |
0 |
40 |
110 |
20 |
0 |
50 |
40 |
0 |
|
|||||
14 |
65 |
0 |
10 |
15 |
0 |
0 |
80 |
40 |
50 |
100 |
0 |
35 |
40 |
0 |
50 |
10 |
50 |
15 |
|
|||||
15 |
80 |
0 |
0 |
55 |
50 |
45 |
10 |
25 |
40 |
65 |
45 |
0 |
90 |
20 |
35 |
50 |
0 |
35 |
|
|||||
16 |
80 |
50 |
0 |
55 |
0 |
45 |
10 |
10 |
45 |
70 |
0 |
0 |
90 |
25 |
40 |
40 |
50 |
40 |
|
|||||
17 |
90 |
45 |
25 |
65 |
0 |
50 |
40 |
45 |
10 |
60 |
35 |
55 |
95 |
0 |
5 |
55 |
0 |
5 |
|
|||||
18 |
95 |
40 |
25 |
70 |
45 |
40 |
45 |
15 |
0 |
45 |
50 |
40 |
105 |
30 |
0 |
75 |
10 |
0 |
|
|||||
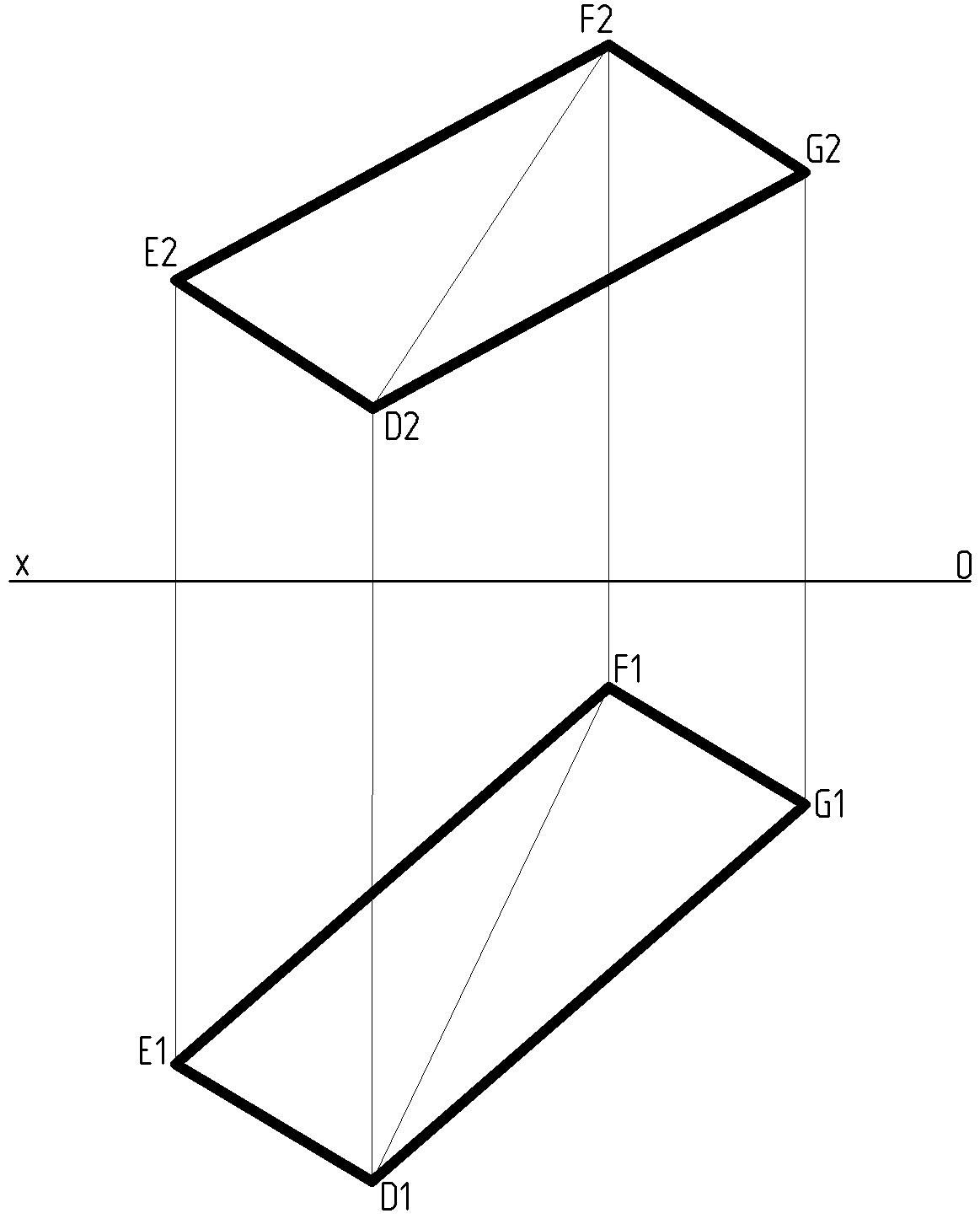
Рисунок 3 – Пример построения
4. Построить ортогональный чертеж плоскости общего положения Р, заданной следами. Исходные данные взять из таблицы 4. Значение А соответствует координате по оси Х для определения точки схода следов искомой плоскости.
Таблица 4
№ варианта |
Плоскость Р |
А |
||
α |
β |
|||
Град. |
||||
1 |
70 |
40 |
120 |
|
2 |
60 |
70 |
130 |
|
3 |
60 |
60 |
130 |
|
4 |
75 |
40 |
125 |
|
5 |
68 |
39 |
135 |
|
6 |
76 |
50 |
120 |
|
7 |
80 |
45 |
130 |
|
8 |
48 |
66 |
130 |
|
9 |
54 |
58 |
125 |
|
10 |
42 |
64 |
130 |
|
11 |
74 |
49 |
125 |
|
12 |
81 |
46 |
135 |
|
13 |
60 |
65 |
135 |
|
14 |
48 |
74 |
125 |
|
15 |
73 |
55 |
135 |
|
16 |
49 |
65 |
125 |
|
17 |
62 |
59 |
130 |
|
18 |
75 |
50 |
135 |
|
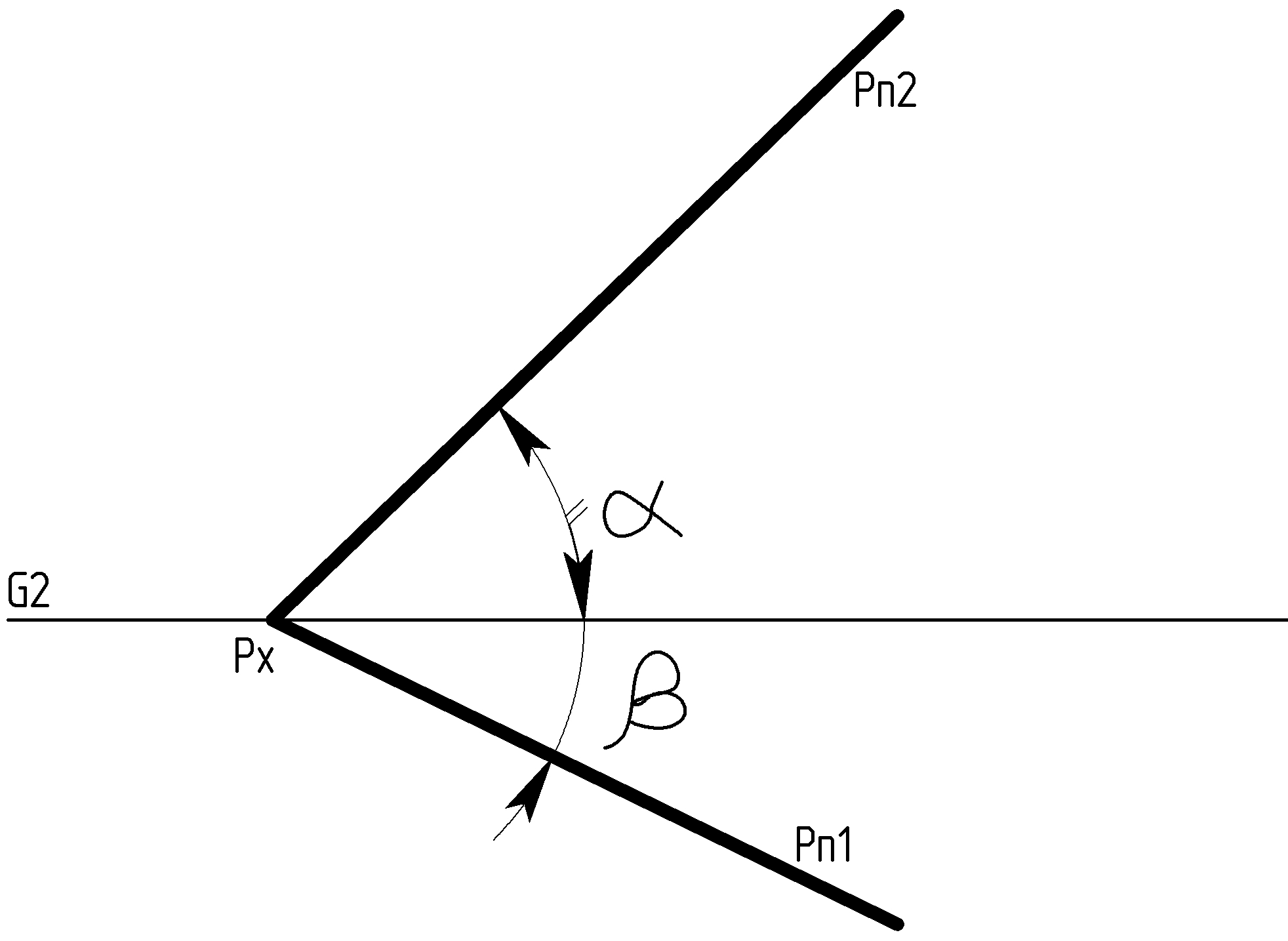
Рисунок 4 – Пример построения
5. Построить ортогональный чертеж плоскости, перпендикулярной горизонтальной плоскости проекций П1. Плоскость задана плоской фигурой (см. таблицу 5). Перейти от задания плоскости плоской фигурой к заданию ее следами.
Таблица 5
№ варианта |
А |
В |
С |
||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
1 |
149 |
42 |
43 |
102 |
10 |
92 |
112 |
- |
46 |
2 |
140 |
39 |
85 |
81 |
13 |
75 |
116 |
- |
33 |
3 |
90 |
12 |
70 |
40 |
50 |
93 |
78 |
- |
30 |
4 |
140 |
52 |
76 |
82 |
9 |
68 |
116 |
- |
43 |
5 |
90 |
22 |
100 |
40 |
60 |
73 |
78 |
- |
32 |
6 |
82 |
16 |
96 |
27 |
43 |
86 |
47 |
- |
40 |
№ варианта |
А |
В |
С |
D |
||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
7 |
157 |
50 |
17 |
157 |
50 |
75 |
120 |
20 |
81 |
120 |
20 |
40 |
8 |
153 |
41 |
20 |
142 |
- |
78 |
126 |
- |
71 |
120 |
18 |
30 |
9 |
71 |
11 |
41 |
68 |
- |
75 |
20 |
40 |
84 |
34 |
- |
20 |
10 |
80 |
6 |
50 |
57 |
- |
90 |
20 |
30 |
44 |
46 |
- |
28 |
11 |
163 |
42 |
64 |
123 |
- |
80 |
112 |
6 |
59 |
142 |
- |
25 |
12 |
135 |
62 |
40 |
120 |
- |
80 |
70 |
6 |
50 |
102 |
- |
10 |
№ варианта |
А |
В |
С |
D |
E |
||||||||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|||||
13 |
84 |
14 |
70 |
37 |
- |
87 |
19 |
76 |
50 |
45 |
- |
18 |
70 |
- |
25 |
||||
14 |
150 |
56 |
40 |
144 |
- |
82 |
103 |
- |
90 |
98 |
8 |
55 |
123 |
- |
16 |
||||
15 |
99 |
13 |
41 |
75 |
- |
96 |
37 |
76 |
72 |
46 |
- |
33 |
91 |
- |
20 |
||||
16 |
146 |
45 |
65 |
133 |
- |
95 |
83 |
10 |
77 |
87 |
- |
46 |
124 |
- |
10 |
||||
17 |
102 |
11 |
80 |
75 |
- |
110 |
52 |
- |
94 |
45 |
42 |
70 |
85 |
- |
27 |
||||
18 |
141 |
30 |
57 |
96 |
|
100 |
55 |
9 |
62 |
110 |
- |
28 |
130 |
- |
37 |
||||
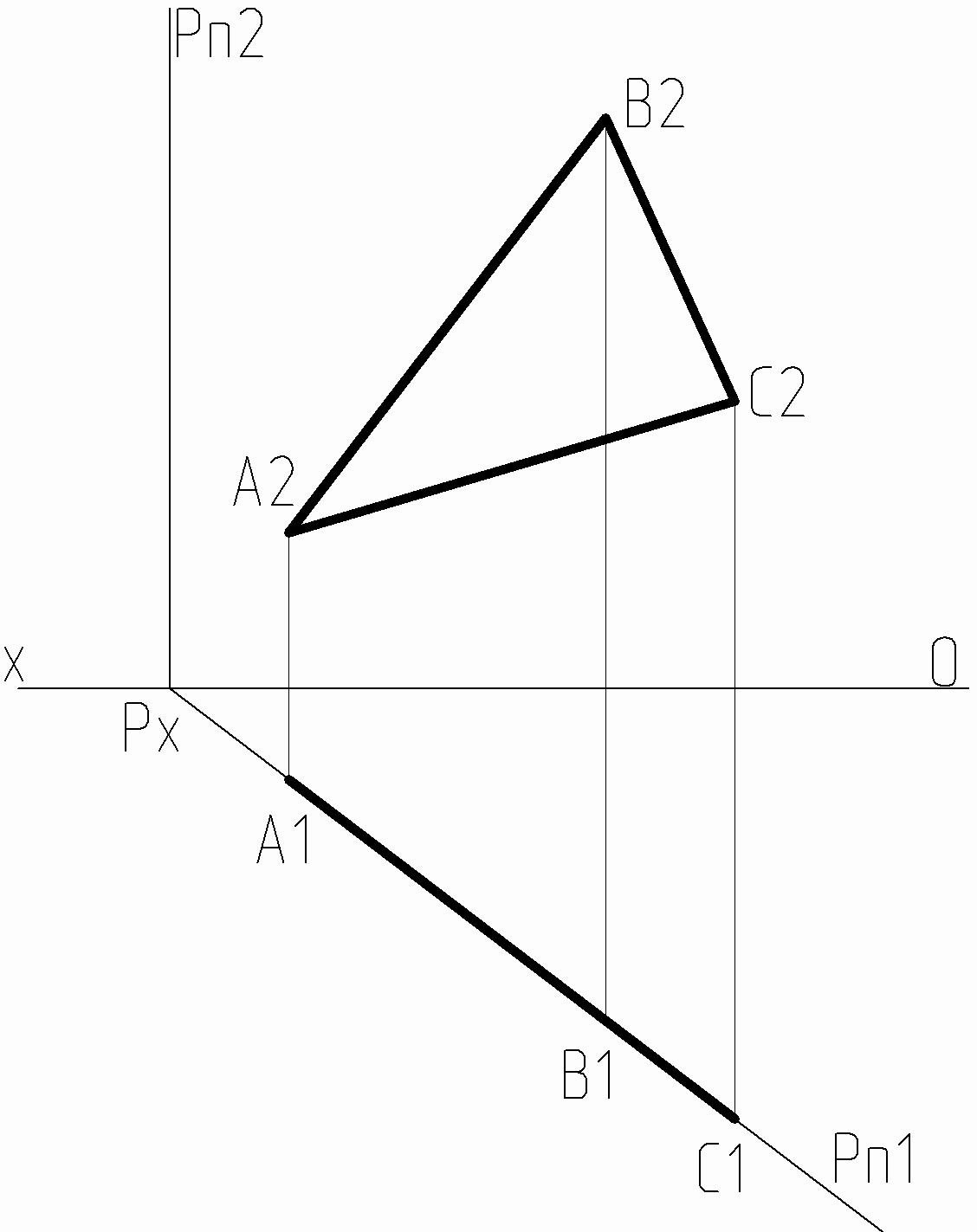
Рисунок 5 – Пример построения
6. Построить горизонтальную проекцию точки К, принадлежащей плоскости треугольника АВС. Через точку М провести прямую МN, параллельную плоскости треугольника АВС.
Координаты вершин треугольника АВС и точек M и K взять из таблицы 7, приведенной ниже.
Таблица 7 – Исходные данные
№ варианта |
А |
В |
С |
||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
1 |
55 |
50 |
50 |
15 |
25 |
0 |
95 |
0 |
15 |
2 |
95 |
0 |
20 |
65 |
55 |
50 |
15 |
40 |
0 |
3 |
110 |
35 |
10 |
45 |
0 |
50 |
20 |
55 |
10 |
4 |
50 |
45 |
35 |
20 |
30 |
20 |
95 |
10 |
0 |
5 |
25 |
50 |
0 |
40 |
10 |
50 |
95 |
35 |
0 |
6 |
85 |
50 |
40 |
15 |
20 |
40 |
110 |
50 |
0 |
7 |
100 |
0 |
0 |
80 |
35 |
40 |
20 |
50 |
35 |
8 |
60 |
5 |
40 |
90 |
55 |
0 |
15 |
15 |
0 |
9 |
10 |
15 |
0 |
80 |
65 |
50 |
90 |
5 |
0 |
10 |
15 |
15 |
20 |
70 |
50 |
50 |
100 |
0 |
0 |
11 |
115 |
20 |
0 |
10 |
55 |
0 |
35 |
5 |
45 |
12 |
90 |
5 |
45 |
10 |
40 |
25 |
75 |
55 |
0 |
13 |
105 |
35 |
15 |
70 |
50 |
55 |
30 |
5 |
15 |
14 |
65 |
0 |
10 |
15 |
0 |
0 |
80 |
40 |
50 |
15 |
80 |
0 |
0 |
55 |
50 |
45 |
10 |
25 |
40 |
16 |
80 |
50 |
0 |
55 |
0 |
45 |
10 |
10 |
45 |
17 |
90 |
45 |
25 |
65 |
0 |
50 |
40 |
45 |
10 |
18 |
95 |
40 |
25 |
70 |
45 |
40 |
45 |
15 |
0 |
№ варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||||||||
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
|
X |
70 |
15 |
65 |
30 |
50 |
95 |
75 |
20 |
40 |
80 |
80 |
100 |
75 |
20 |
65 |
30 |
60 |
100 |
Y |
- |
15 |
- |
25 |
- |
50 |
- |
10 |
- |
50 |
- |
15 |
- |
50 |
- |
45 |
- |
10 |
Z |
30 |
35 |
30 |
50 |
20 |
40 |
10 |
0 |
20 |
35 |
25 |
5 |
25 |
35 |
15 |
25 |
10 |
10 |
№ варианта |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|||||||||
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
К |
М |
|
X |
60 |
95 |
40 |
95 |
60 |
20 |
70 |
30 |
65 |
10 |
45 |
25 |
50 |
20 |
75 |
30 |
80 |
15 |
Y |
- |
45 |
- |
55 |
- |
55 |
- |
40 |
- |
50 |
- |
25 |
- |
25 |
- |
45 |
- |
30 |
Z |
30 |
0 |
25 |
50 |
30 |
45 |
35 |
0 |
20 |
15 |
30 |
0 |
35 |
0 |
30 |
10 |
25 |
40 |
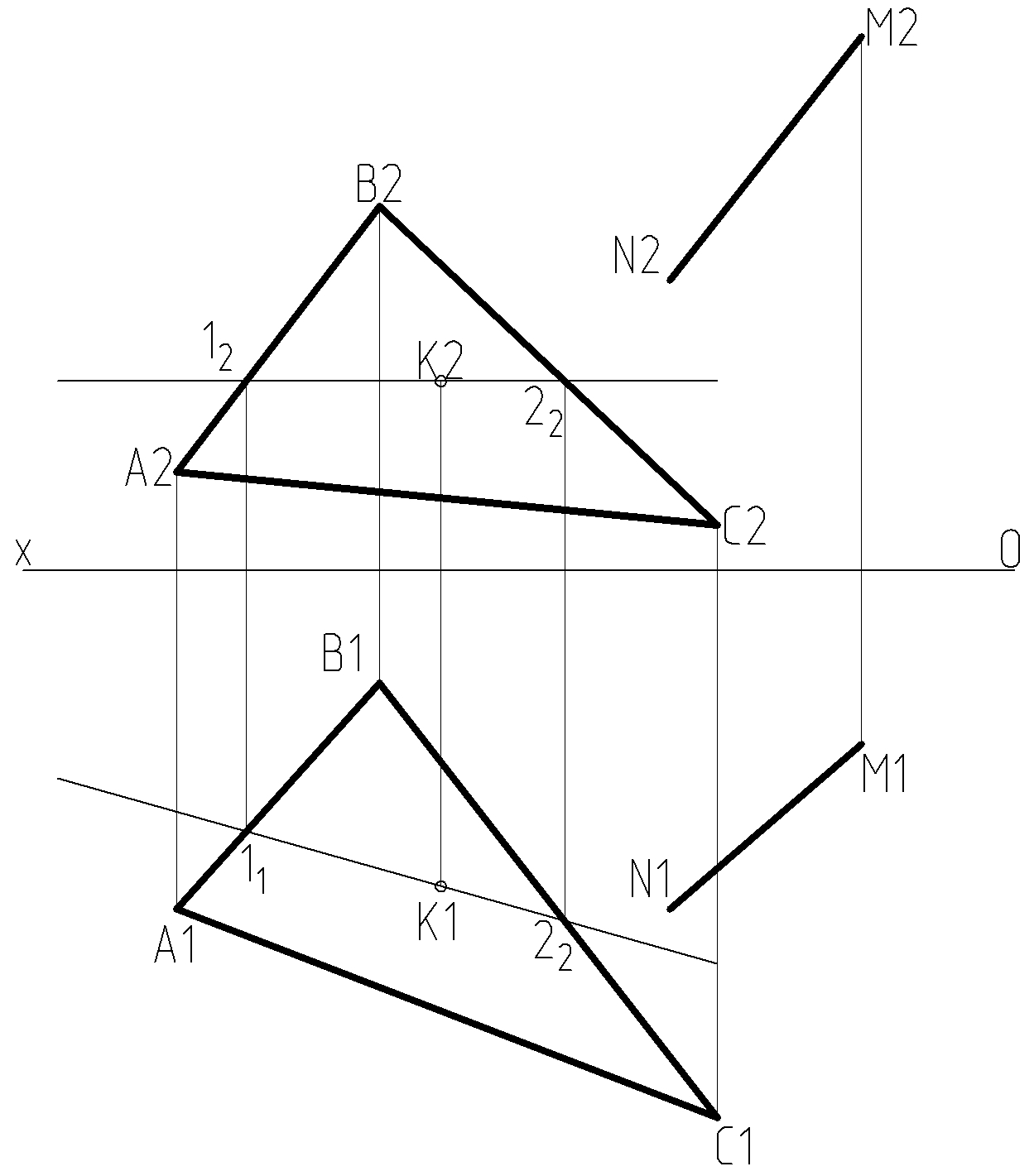
Рисунок 6 – Пример построения
7. На ортогональном чертеже построить построить линию пересечения двух плоскостей P и Q, заданных следами (см. таблицу 7).
Для правильного размещения чертежа ось OX провести на расстоянии А от поверхностей рамки чертежа, а расстояния от правой и левой линий рамки до точек Px и Qx сделать одинаковыми.
Таблица 7 – Исходные данные
№ варианта |
Плоскость P |
Плоскость Q |
A |
||
α |
β |
α1 |
β1 |
||
Град. |
|||||
1 |
70 |
40 |
55 |
60 |
120 |
2 |
60 |
70 |
65 |
40 |
130 |
3 |
60 |
60 |
55 |
45 |
130 |
4 |
75 |
40 |
45 |
73 |
125 |
5 |
68 |
39 |
52 |
76 |
135 |
6 |
76 |
50 |
46 |
72 |
120 |
7 |
80 |
45 |
45 |
75 |
130 |
8 |
48 |
66 |
76 |
40 |
130 |
9 |
54 |
58 |
70 |
56 |
125 |
10 |
42 |
64 |
82 |
47 |
130 |
11 |
74 |
49 |
50 |
70 |
125 |
12 |
81 |
46 |
45 |
60 |
135 |
13 |
60 |
65 |
60 |
35 |
135 |
14 |
48 |
74 |
76 |
46 |
125 |
15 |
73 |
65 |
45 |
60 |
135 |
16 |
49 |
65 |
77 |
50 |
125 |
17 |
62 |
59 |
60 |
34 |
130 |
18 |
75 |
50 |
48 |
68 |
135 |
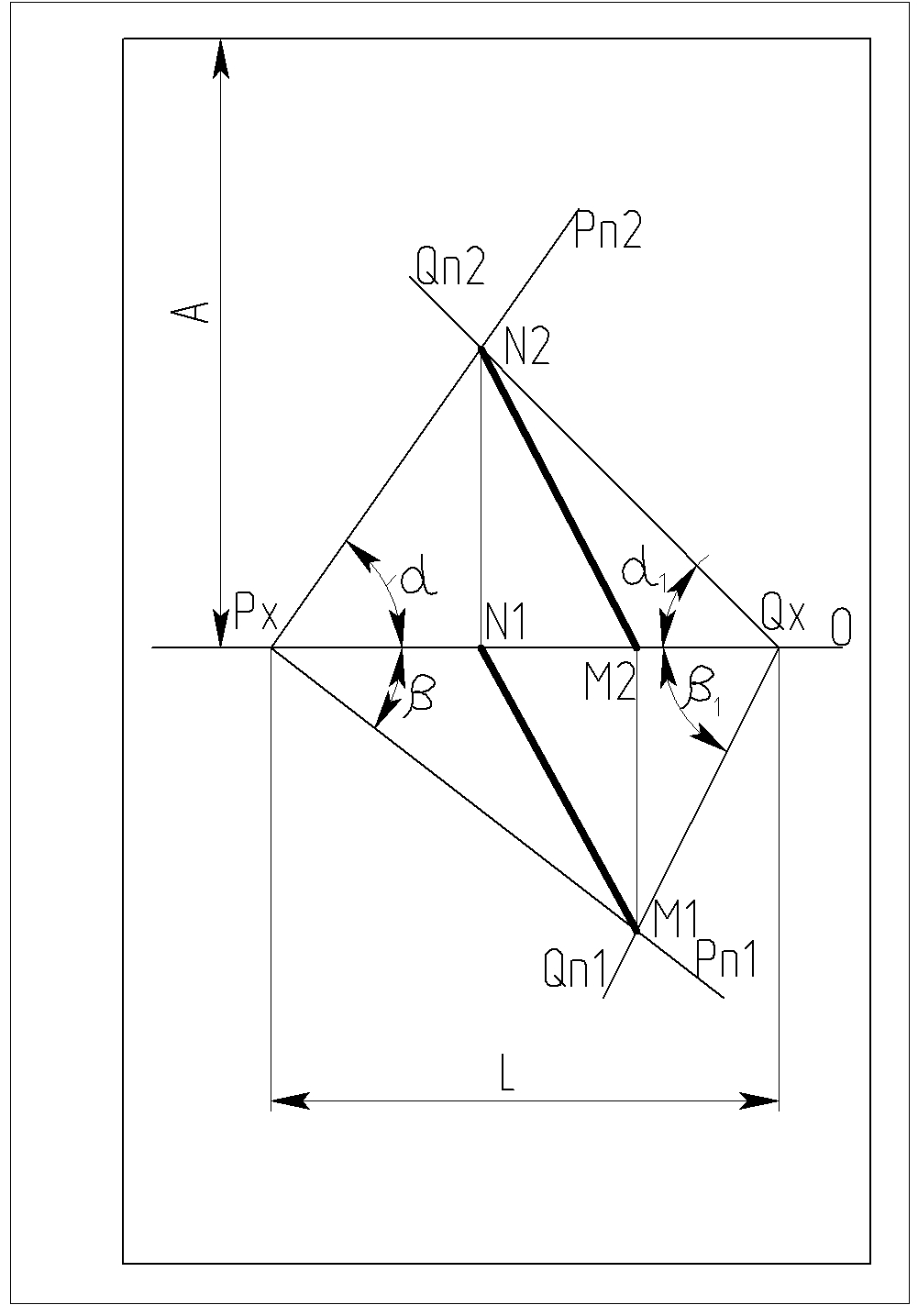
Рисунок 7 – Пример построения
8. Построить точку пересечения прямой АВ с плоскостью Р, заданной следами (см. таблицу 8).
Таблица 8 – Исходные данные
№ варианта |
L |
Плоскость Р |
А |
В |
|||||
α |
β |
X |
Y |
Z |
X |
Y |
Z |
||
Град. |
|||||||||
1 |
100 |
45 |
30 |
70 |
30 |
40 |
45 |
10 |
5 |
2 |
100 |
45 |
30 |
60 |
45 |
60 |
40 |
15 |
20 |
3 |
100 |
45 |
30 |
80 |
45 |
35 |
50 |
15 |
20 |
4 |
100 |
45 |
30 |
45 |
50 |
50 |
25 |
15 |
15 |
5 |
100 |
45 |
30 |
55 |
35 |
65 |
10 |
0 |
10 |
6 |
100 |
30 |
45 |
70 |
40 |
30 |
45 |
5 |
10 |
7 |
100 |
30 |
45 |
60 |
60 |
45 |
40 |
20 |
15 |
8 |
100 |
30 |
45 |
80 |
35 |
45 |
50 |
20 |
15 |
9 |
100 |
30 |
45 |
45 |
50 |
50 |
25 |
15 |
15 |
10 |
10 |
30 |
45 |
55 |
65 |
35 |
100 |
10 |
0 |
11 |
10 |
30 |
45 |
65 |
50 |
50 |
85 |
15 |
15 |
12 |
10 |
30 |
45 |
30 |
35 |
45 |
60 |
20 |
15 |
13 |
10 |
30 |
45 |
50 |
60 |
45 |
70 |
20 |
15 |
14 |
10 |
30 |
45 |
40 |
40 |
30 |
65 |
5 |
10 |
15 |
10 |
45 |
30 |
55 |
35 |
65 |
100 |
0 |
10 |
16 |
10 |
45 |
30 |
30 |
45 |
35 |
60 |
15 |
20 |
17 |
10 |
45 |
30 |
50 |
45 |
60 |
70 |
15 |
20 |
18 |
10 |
45 |
30 |
40 |
30 |
40 |
65 |
10 |
5 |

Рисунок 8 – Пример построения
9. Построить точку пересечения прямой АС с плоскостью параллелограмма DEFG (для вариантов 7, 13 – 16, 18), прямой DF с плоскостью треугольника АВС (для вариантов 1 – 3, 5, 6, 11 и 17), прямой DF с плоскостью треугольника DEF (для варианта 4) – см. таблицу 9. Основные принципы построения и оформления чертежа смотреть на рисунке 9.
Таблица 9 – Исходные данные
№ варианта |
A |
B |
C |
D |
E |
F |
||||||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
1 |
55 |
50 |
50 |
15 |
25 |
0 |
95 |
0 |
15 |
15 |
15 |
35 |
85 |
35 |
0 |
50 |
0 |
35 |
2 |
95 |
0 |
20 |
65 |
55 |
50 |
15 |
40 |
0 |
30 |
25 |
50 |
55 |
45 |
0 |
85 |
0 |
40 |
3 |
110 |
35 |
10 |
45 |
0 |
50 |
20 |
55 |
10 |
95 |
50 |
40 |
50 |
10 |
0 |
15 |
25 |
10 |
4 |
50 |
45 |
35 |
20 |
30 |
20 |
95 |
10 |
0 |
20 |
10 |
0 |
95 |
20 |
0 |
75 |
50 |
0 |
5 |
25 |
50 |
0 |
40 |
10 |
50 |
95 |
35 |
0 |
50 |
0 |
0 |
80 |
50 |
35 |
20 |
15 |
15 |
6 |
85 |
50 |
40 |
15 |
20 |
40 |
110 |
5 |
0 |
100 |
15 |
50 |
70 |
50 |
0 |
40 |
35 |
20 |
7 |
100 |
0 |
0 |
80 |
35 |
40 |
20 |
50 |
35 |
85 |
45 |
0 |
115 |
0 |
30 |
50 |
0 |
30 |
8 |
60 |
5 |
40 |
90 |
55 |
0 |
15 |
15 |
0 |
90 |
10 |
5 |
75 |
0 |
25 |
30 |
45 |
25 |
9 |
10 |
15 |
0 |
80 |
55 |
50 |
90 |
5 |
0 |
55 |
45 |
0 |
100 |
10 |
35 |
70 |
10 |
35 |
10 |
15 |
15 |
20 |
70 |
50 |
50 |
100 |
0 |
0 |
95 |
45 |
0 |
60 |
0 |
45 |
20 |
0 |
45 |
11 |
115 |
20 |
0 |
10 |
55 |
0 |
35 |
5 |
45 |
65 |
15 |
0 |
95 |
55 |
50 |
60 |
45 |
50 |
12 |
90 |
5 |
45 |
10 |
40 |
25 |
75 |
55 |
0 |
95 |
5 |
0 |
60 |
5 |
0 |
20 |
55 |
45 |
13 |
105 |
35 |
15 |
70 |
50 |
55 |
30 |
5 |
15 |
70 |
0 |
40 |
110 |
20 |
0 |
50 |
40 |
0 |
14 |
65 |
0 |
10 |
15 |
0 |
0 |
80 |
40 |
50 |
100 |
0 |
35 |
40 |
0 |
50 |
10 |
50 |
15 |
15 |
80 |
0 |
0 |
55 |
50 |
45 |
10 |
25 |
40 |
65 |
45 |
0 |
90 |
20 |
35 |
50 |
0 |
35 |
16 |
80 |
50 |
0 |
55 |
0 |
45 |
10 |
10 |
45 |
70 |
0 |
0 |
90 |
25 |
40 |
40 |
50 |
40 |
17 |
90 |
45 |
25 |
65 |
0 |
50 |
40 |
45 |
10 |
60 |
35 |
55 |
95 |
0 |
5 |
55 |
0 |
5 |
18 |
95 |
40 |
25 |
70 |
45 |
40 |
45 |
15 |
0 |
45 |
50 |
40 |
105 |
30 |
0 |
75 |
10 |
0 |
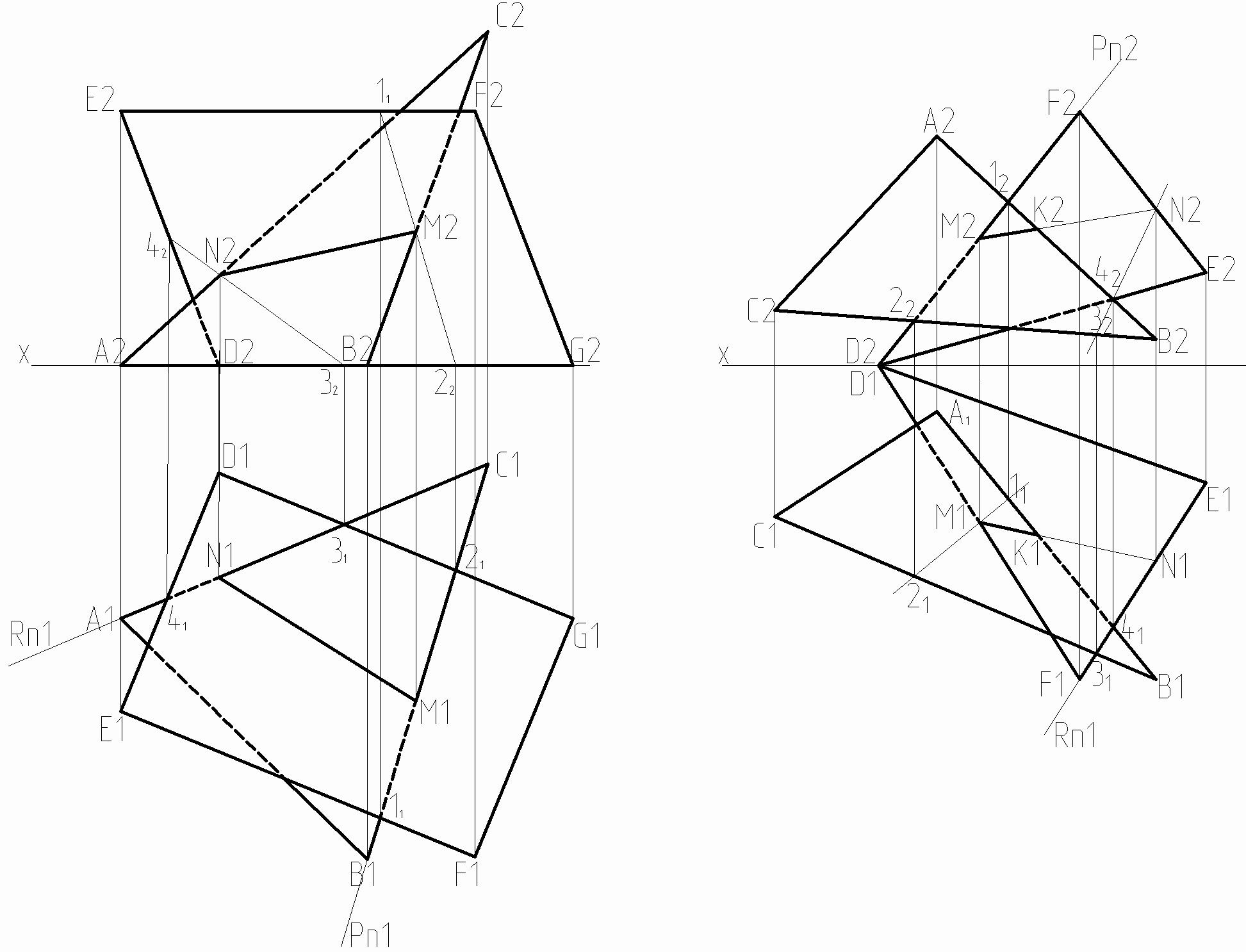
Рисунок 9 – Пример построения
10. Построить линию пересечения двух треугольников: ABC и DEF (варианты 1-6), треугольника АВС и параллелограмма DEFG (варианты 7 – 18). За диагональ параллелограмма принять DF. Исходные данные брать из таблицы 9, пример построения приведен на рисунке 9.
11. Определить действительную величину треугольника (варианты 1 – 6, см. таблицу 10), четырехугольника (варианты 7 – 12), и пятиугольника (варианты 13 – 18) способом перемены плоскостей проекций.
Таблица 10
№ варианта |
А |
В |
С |
||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
1 |
149 |
42 |
43 |
102 |
10 |
92 |
112 |
- |
46 |
2 |
140 |
39 |
85 |
81 |
13 |
75 |
116 |
- |
33 |
3 |
90 |
12 |
70 |
40 |
50 |
93 |
78 |
- |
30 |
4 |
140 |
52 |
76 |
82 |
9 |
68 |
116 |
- |
43 |
5 |
90 |
22 |
100 |
40 |
60 |
73 |
78 |
- |
32 |
6 |
82 |
16 |
96 |
27 |
43 |
86 |
47 |
- |
40 |
№ варианта |
А |
В |
С |
D |
||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
7 |
157 |
50 |
17 |
157 |
50 |
75 |
120 |
20 |
81 |
120 |
20 |
40 |
8 |
153 |
41 |
20 |
142 |
- |
78 |
126 |
- |
71 |
120 |
18 |
30 |
9 |
71 |
11 |
41 |
68 |
- |
75 |
20 |
40 |
84 |
34 |
- |
20 |
10 |
80 |
6 |
50 |
57 |
- |
90 |
20 |
30 |
44 |
46 |
- |
28 |
11 |
163 |
42 |
64 |
123 |
- |
80 |
112 |
6 |
59 |
142 |
- |
25 |
12 |
135 |
62 |
40 |
120 |
- |
80 |
70 |
6 |
50 |
102 |
- |
10 |
№ варианта |
А |
В |
С |
D |
E |
||||||||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|||||
13 |
84 |
14 |
70 |
37 |
- |
87 |
19 |
76 |
50 |
45 |
- |
18 |
70 |
- |
25 |
||||
14 |
150 |
56 |
40 |
144 |
- |
82 |
103 |
- |
90 |
98 |
8 |
55 |
123 |
- |
16 |
||||
15 |
99 |
13 |
41 |
75 |
- |
96 |
37 |
76 |
72 |
46 |
- |
33 |
91 |
- |
20 |
||||
16 |
146 |
45 |
65 |
133 |
- |
95 |
83 |
10 |
77 |
87 |
- |
46 |
124 |
- |
10 |
||||
17 |
102 |
11 |
80 |
75 |
- |
110 |
52 |
- |
94 |
45 |
42 |
70 |
85 |
- |
27 |
||||
18 |
141 |
30 |
57 |
96 |
|
100 |
55 |
9 |
62 |
110 |
- |
28 |
130 |
- |
37 |
||||
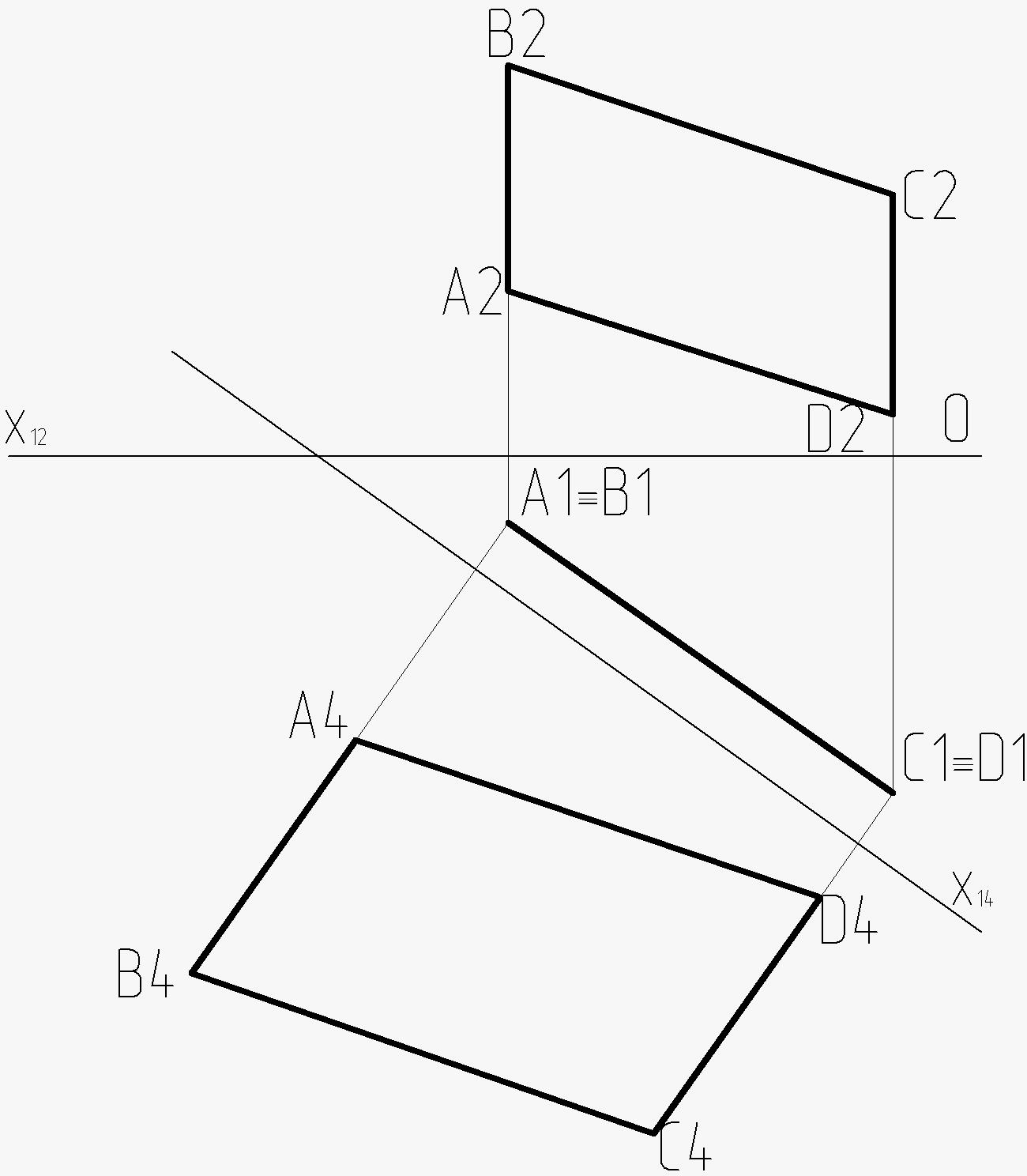
Рисунок 10 – Пример построения
12. Определить действительную величину треугольника (варианты 7 – 12, см. таблицу 11), четырехугольника (варианты 13 – 18) и пятиугольника (варианты 1 – 6) способом вращения (совмещения).
Таблица 11
№ Варианта |
K |
M |
N |
P |
L |
||||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
1 |
147 |
62 |
85 |
131 |
- |
102 |
116 |
20 |
74 |
126 |
- |
48 |
140 |
- |
56 |
2 |
170 |
63 |
55 |
140 |
- |
90 |
120 |
12 |
64 |
135 |
- |
15 |
154 |
- |
20 |
3 |
165 |
67 |
18 |
145 |
- |
93 |
128 |
- |
97 |
114 |
10 |
60 |
123 |
- |
30 |
4 |
72 |
10 |
30 |
59 |
- |
95 |
43 |
- |
114 |
17 |
60 |
38 |
37 |
- |
10 |
5 |
74 |
12 |
10 |
65 |
- |
68 |
60 |
- |
87 |
44 |
- |
94 |
33 |
70 |
18 |
6 |
58 |
15 |
65 |
40 |
- |
98 |
22 |
- |
90 |
7 |
45 |
28 |
30 |
- |
20 |
№ Варианта |
K |
M |
N |
|
|||||||||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|||||||||||
7 |
150 |
56 |
38 |
102 |
8 |
65 |
112 |
- |
31 |
|
|||||||||
8 |
82 |
6 |
57 |
26 |
48 |
102 |
48 |
- |
37 |
|
|||||||||
9 |
153 |
65 |
48 |
118 |
20 |
116 |
133 |
- |
30 |
|
|||||||||
10 |
82 |
7 |
94 |
27 |
48 |
85 |
47 |
- |
40 |
|
|||||||||
11 |
152 |
77 |
91 |
118 |
20 |
110 |
134 |
- |
20 |
|
|||||||||
12 |
78 |
8 |
42 |
19 |
41 |
110 |
34 |
- |
21 |
|
|||||||||
№ Варианта |
E |
K |
M |
N |
||||||||
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
X |
Y |
Z |
|
13 |
164 |
142 |
48 |
146 |
- |
74 |
115 |
15 |
55 |
150 |
- |
17 |
14 |
63 |
17 |
90 |
24 |
- |
76 |
14 |
65 |
48 |
52 |
- |
23 |
15 |
165 |
62 |
34 |
135 |
- |
100 |
112 |
10 |
66 |
149 |
- |
18 |
16 |
67 |
9 |
56 |
43 |
- |
97 |
10 |
56 |
70 |
40 |
- |
15 |
17 |
161 |
36 |
70 |
109 |
10 |
89 |
116 |
- |
55 |
144 |
- |
30 |
18 |
73 |
6 |
72 |
26 |
- |
88 |
8 |
52 |
50 |
35 |
- |
18 |
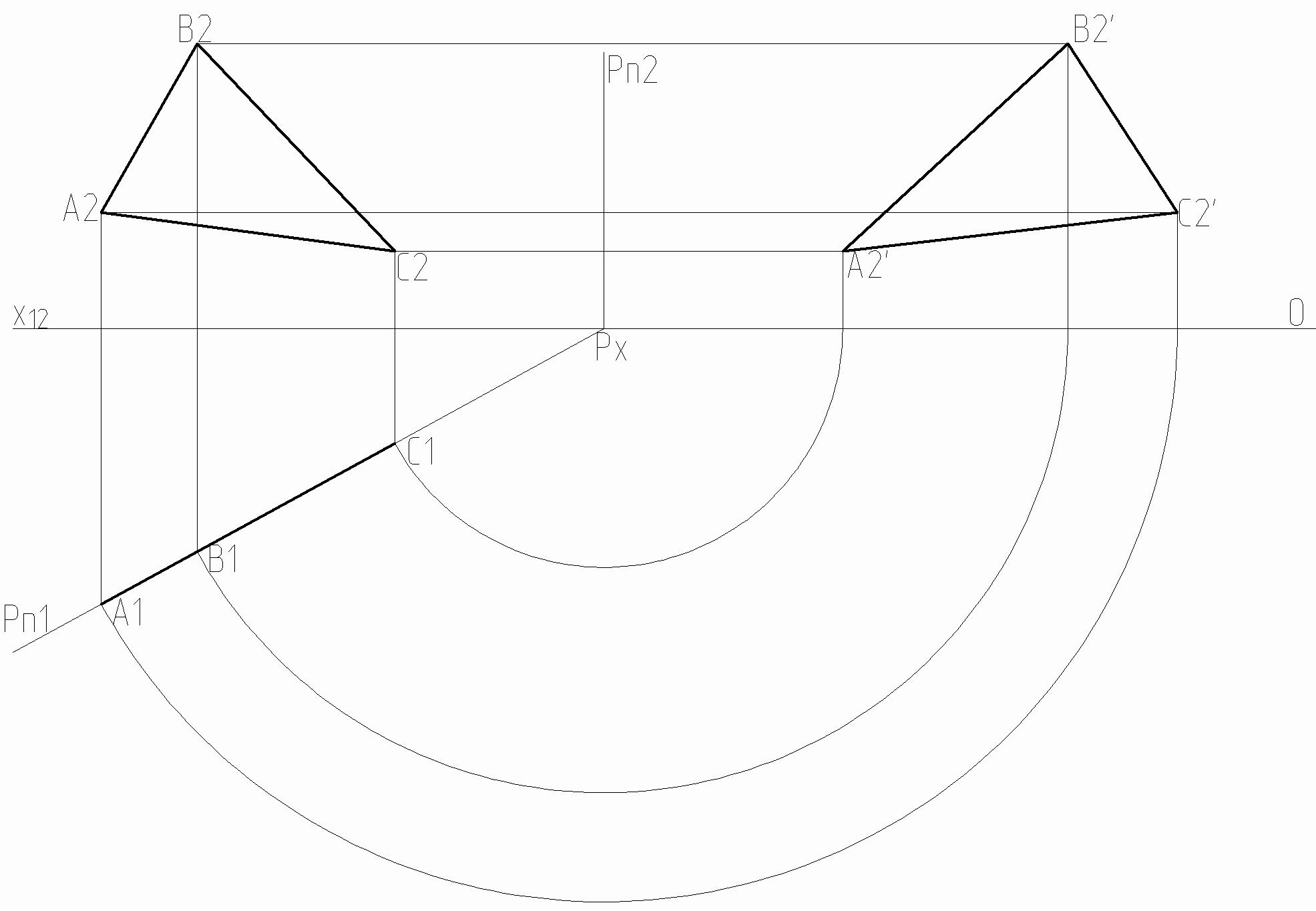
Рисунок 11.1 – Пример построения
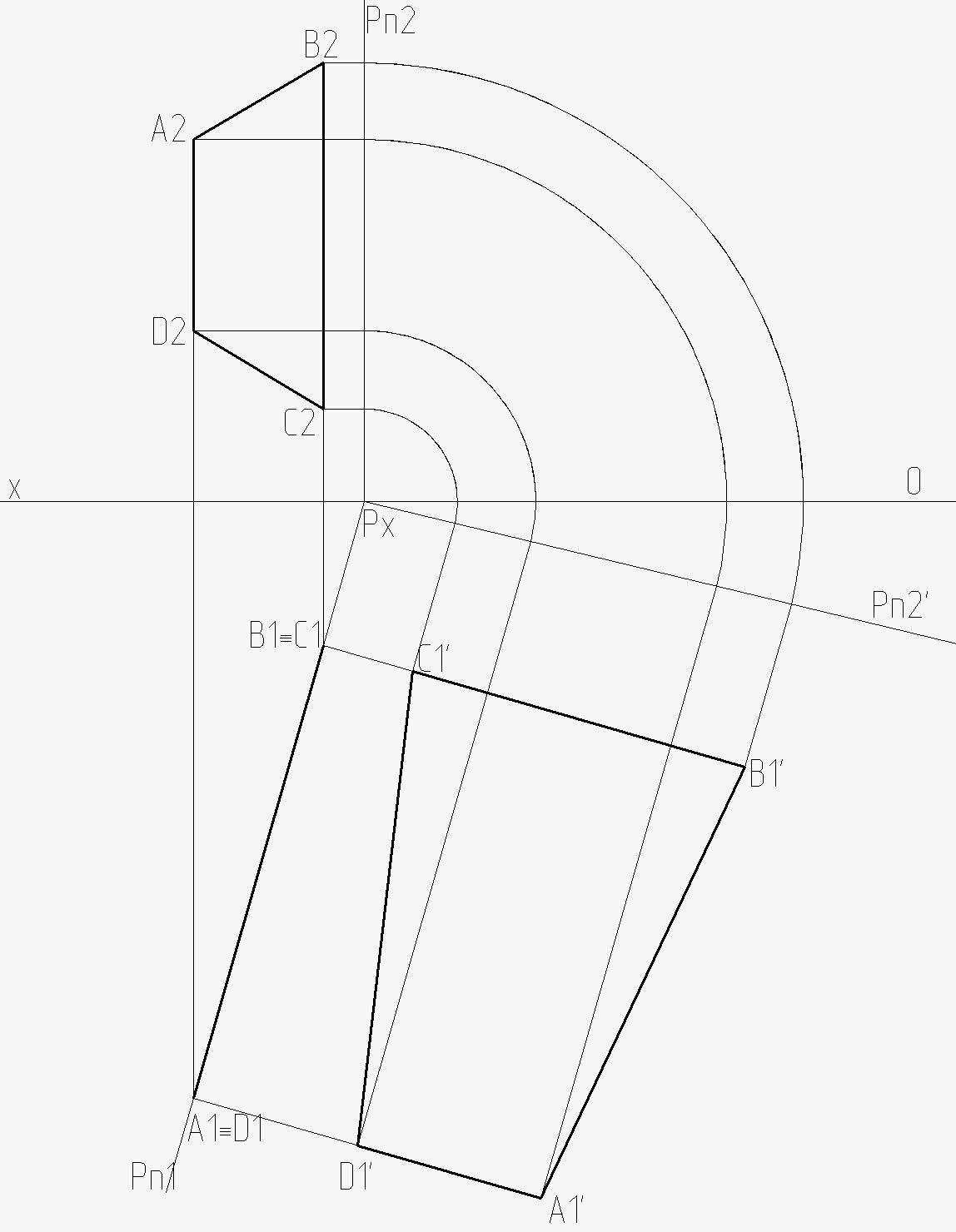
Рисунок 11.2 – Пример построения
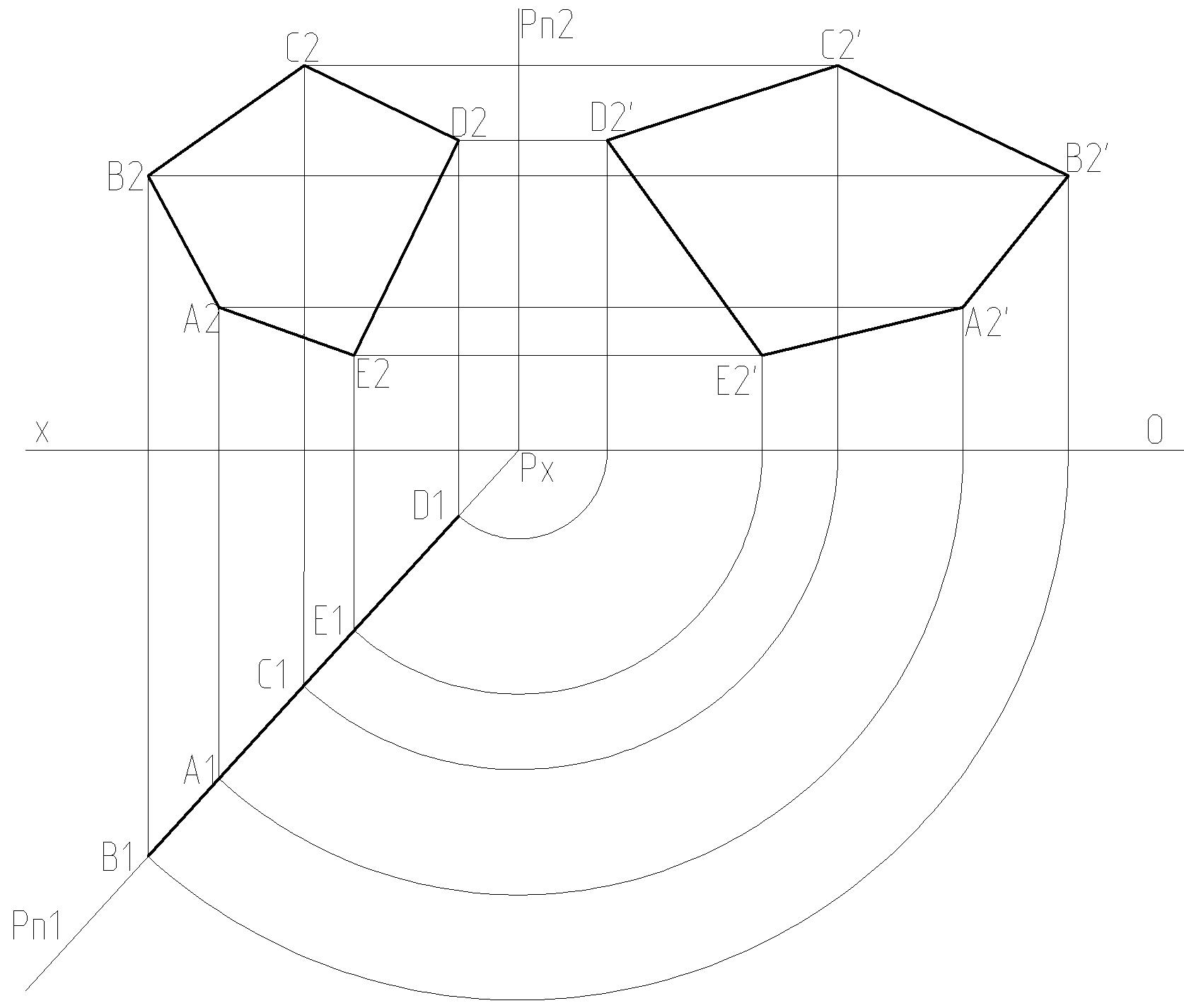
Рисунок 11.3 – Пример построения
13. Определить действительную величину отрезка АВ (см. таблицу 12) прямой общего положения и углов его наклона к плоскостям проекций: α – к плоскости П1 и β – к плоскости П2.
Таблица 12
№ Варианта |
А |
В |
||||
X |
Y |
Z |
X |
Y |
Z |
|
1 |
145 |
56 |
62 |
108 |
22 |
25 |
2 |
84 |
45 |
23 |
25 |
72 |
87 |
3 |
125 |
72 |
96 |
92 |
20 |
32 |
4 |
80 |
54 |
51 |
20 |
72 |
90 |
5 |
130 |
72 |
78 |
88 |
22 |
25 |
6 |
93 |
46 |
17 |
38 |
92 |
65 |
7 |
138 |
71 |
65 |
86 |
32 |
16 |
8 |
94 |
57 |
11 |
25 |
102 |
36 |
9 |
154 |
78 |
67 |
88 |
26 |
45 |
10 |
73 |
18 |
21 |
17 |
75 |
53 |
11 |
120 |
62 |
90 |
102 |
18 |
36 |
12 |
77 |
38 |
42 |
19 |
64 |
110 |
13 |
138 |
58 |
73 |
91 |
27 |
15 |
14 |
85 |
46 |
27 |
35 |
85 |
84 |
15 |
134 |
98 |
75 |
95 |
52 |
11 |
16 |
90 |
48 |
26 |
37 |
106 |
88 |
17 |
150 |
69 |
84 |
89 |
47 |
30 |
18 |
67 |
60 |
24 |
20 |
92 |
106 |
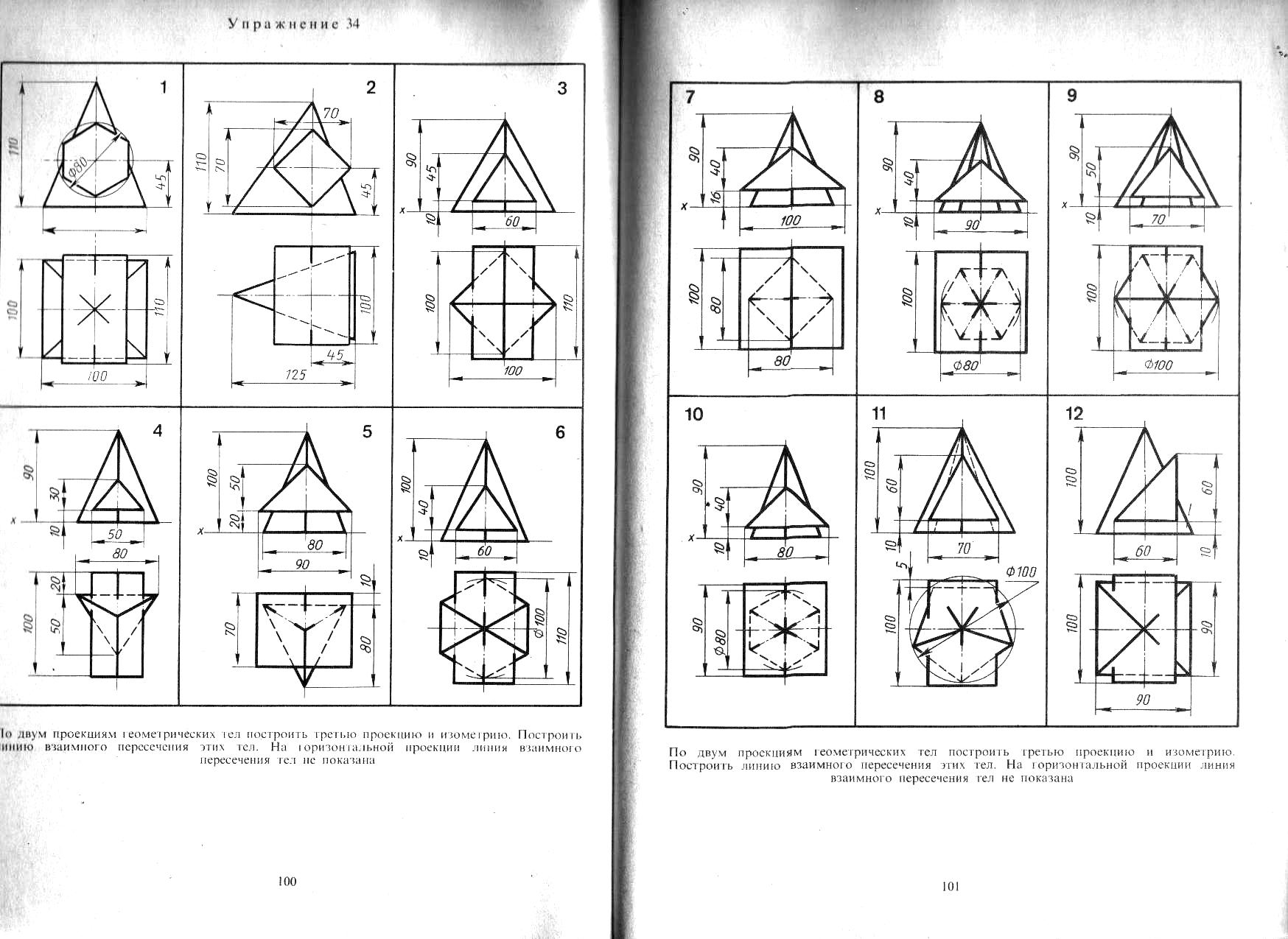
14. По двум проекциям геометрических тел построить третью проекцию. Построить линию взаимного пересечения этих тел.На рисунке 12 приведен пример построения, исходные данные по вариантам смотреть в Приложении 1.На горизонтальной проекции линия пересечения тел не показана.
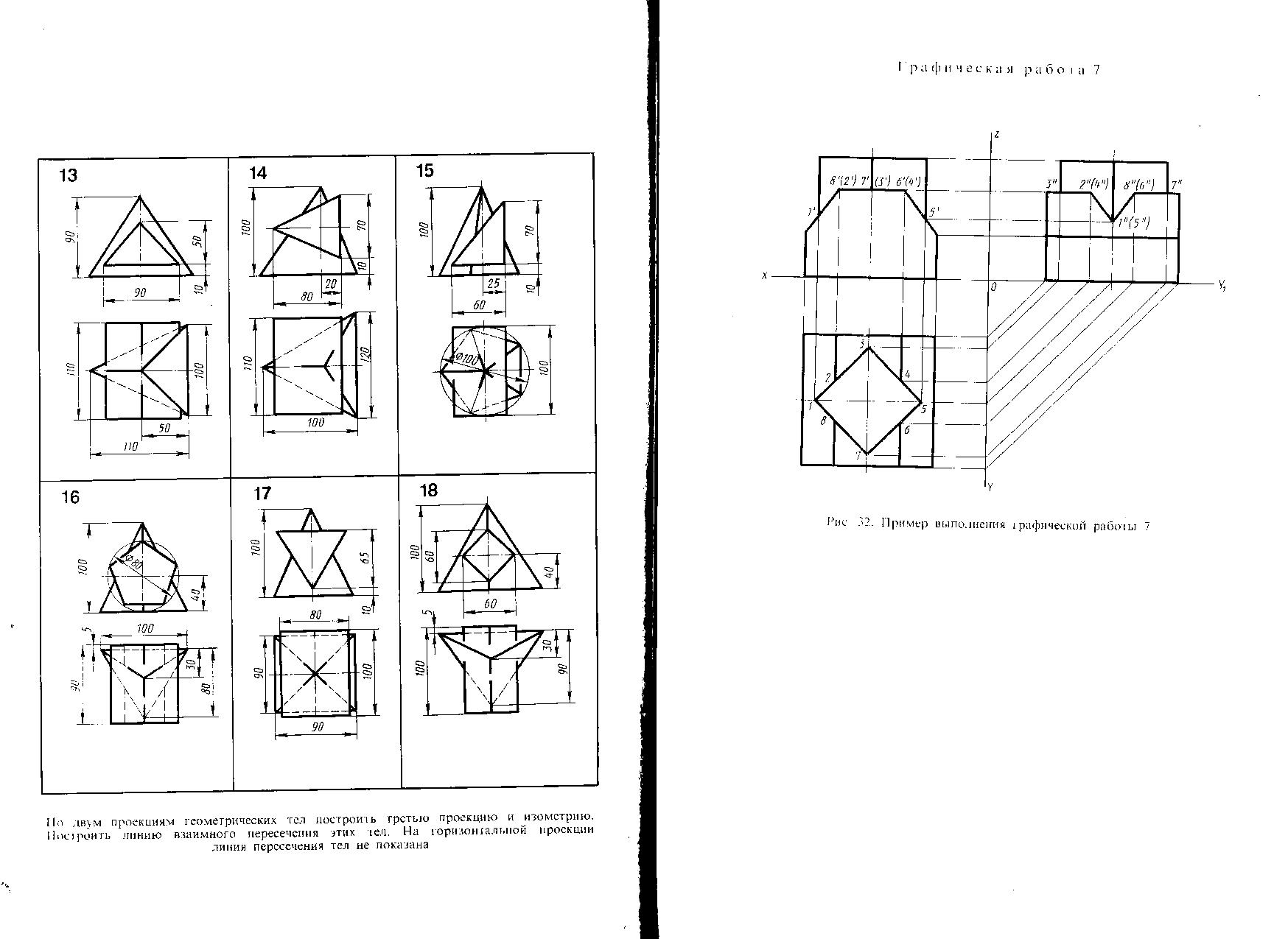 Рисунок
12 – Пример построения
Рисунок
12 – Пример построения
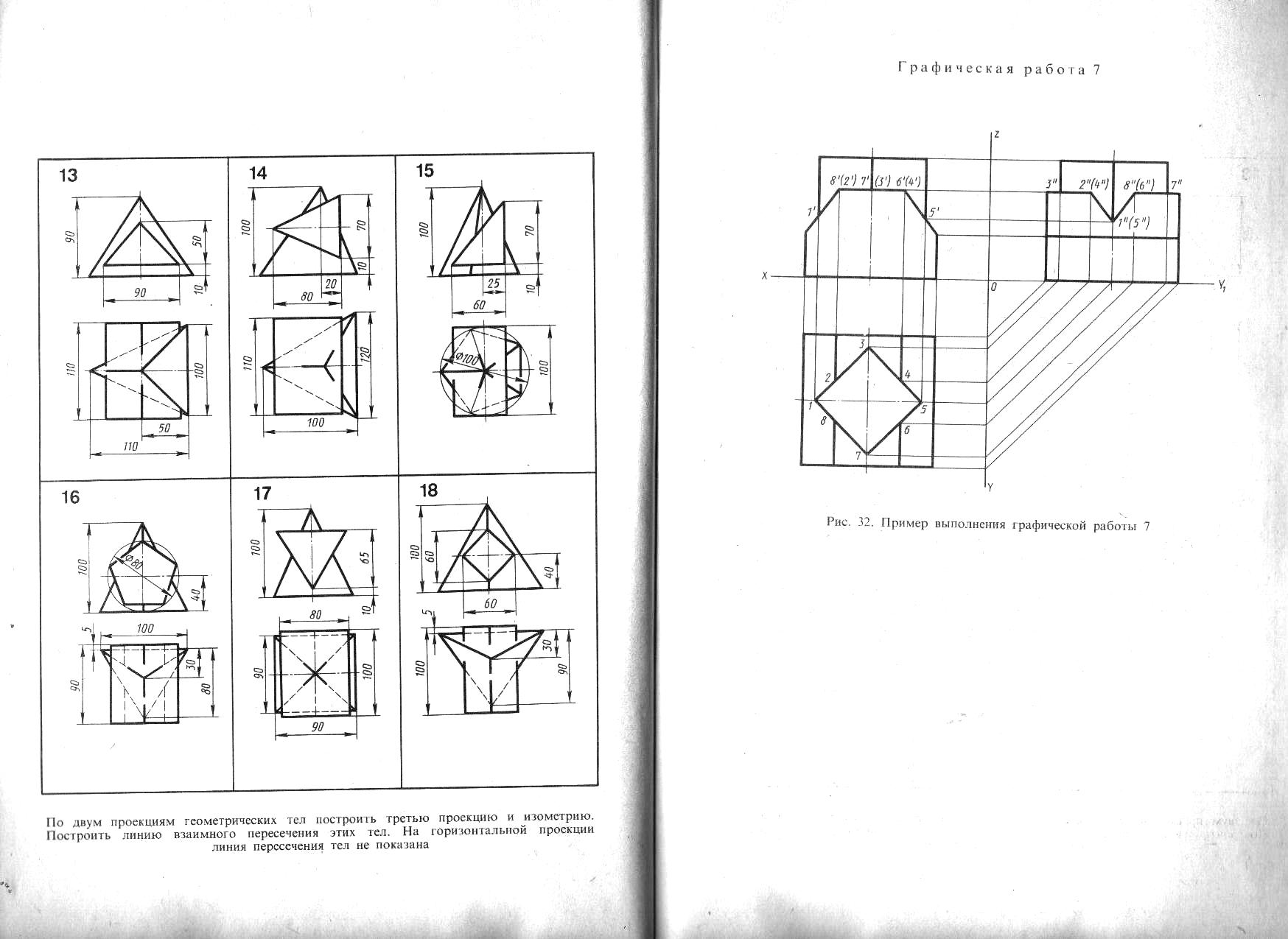
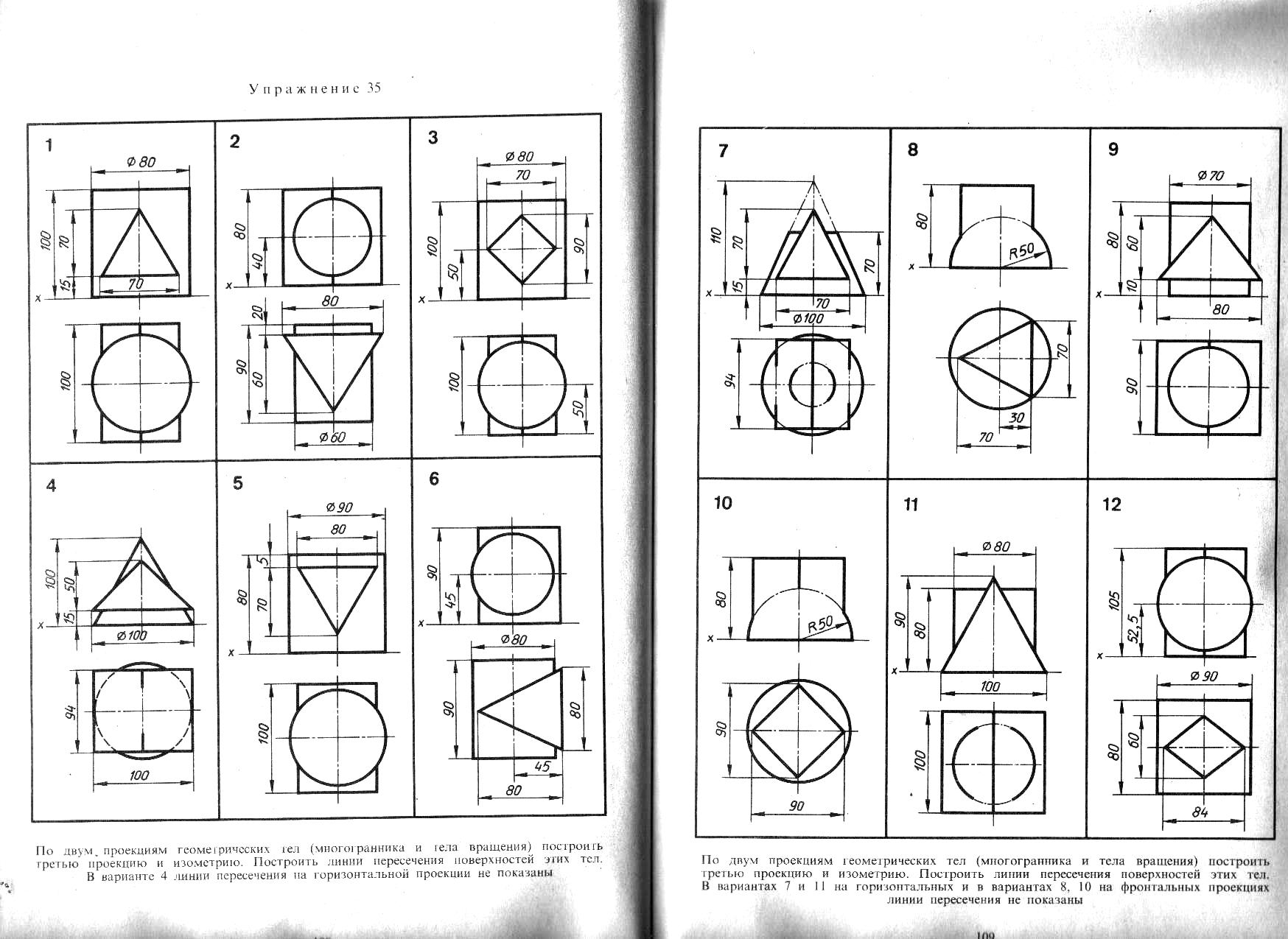
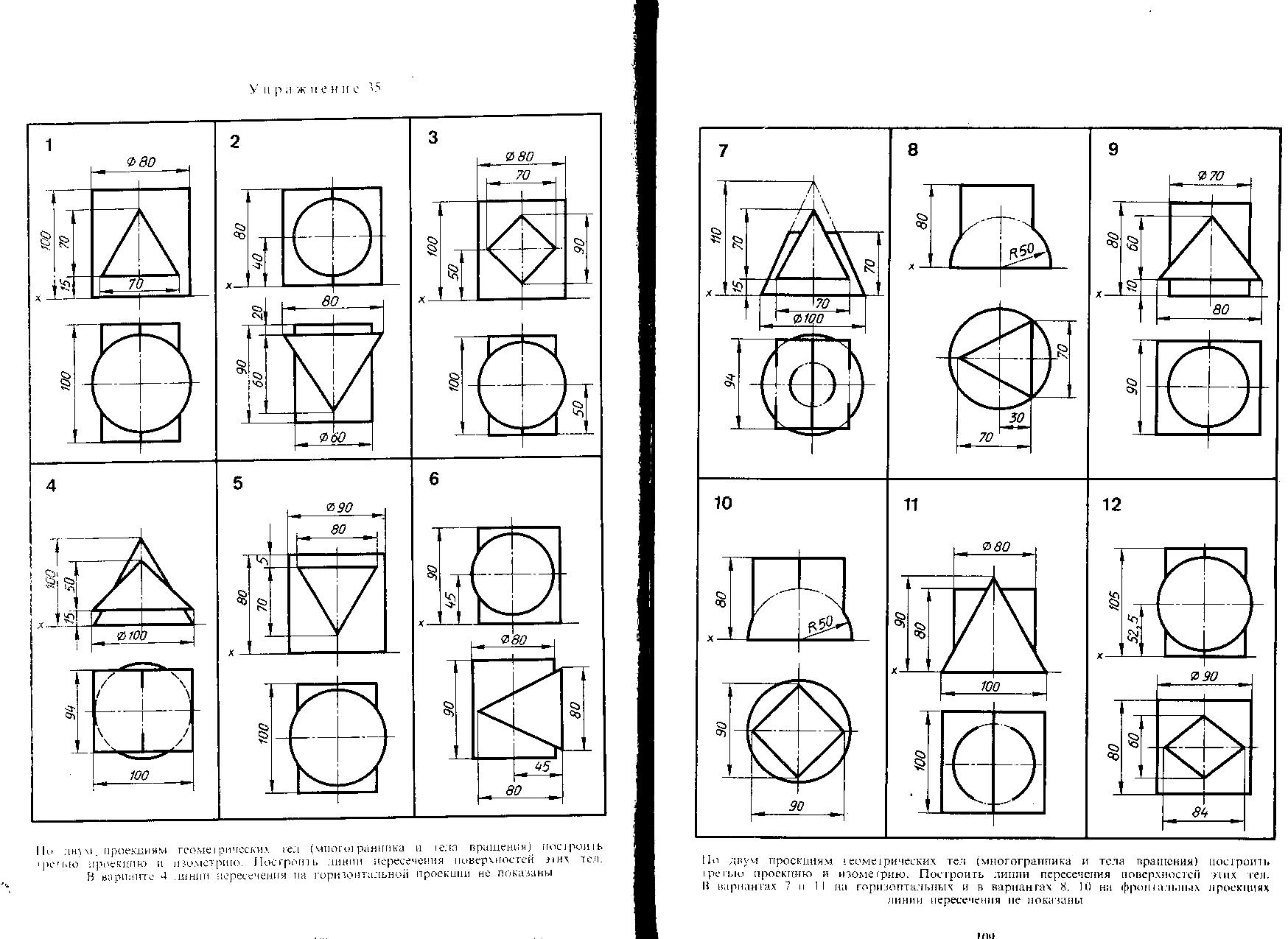
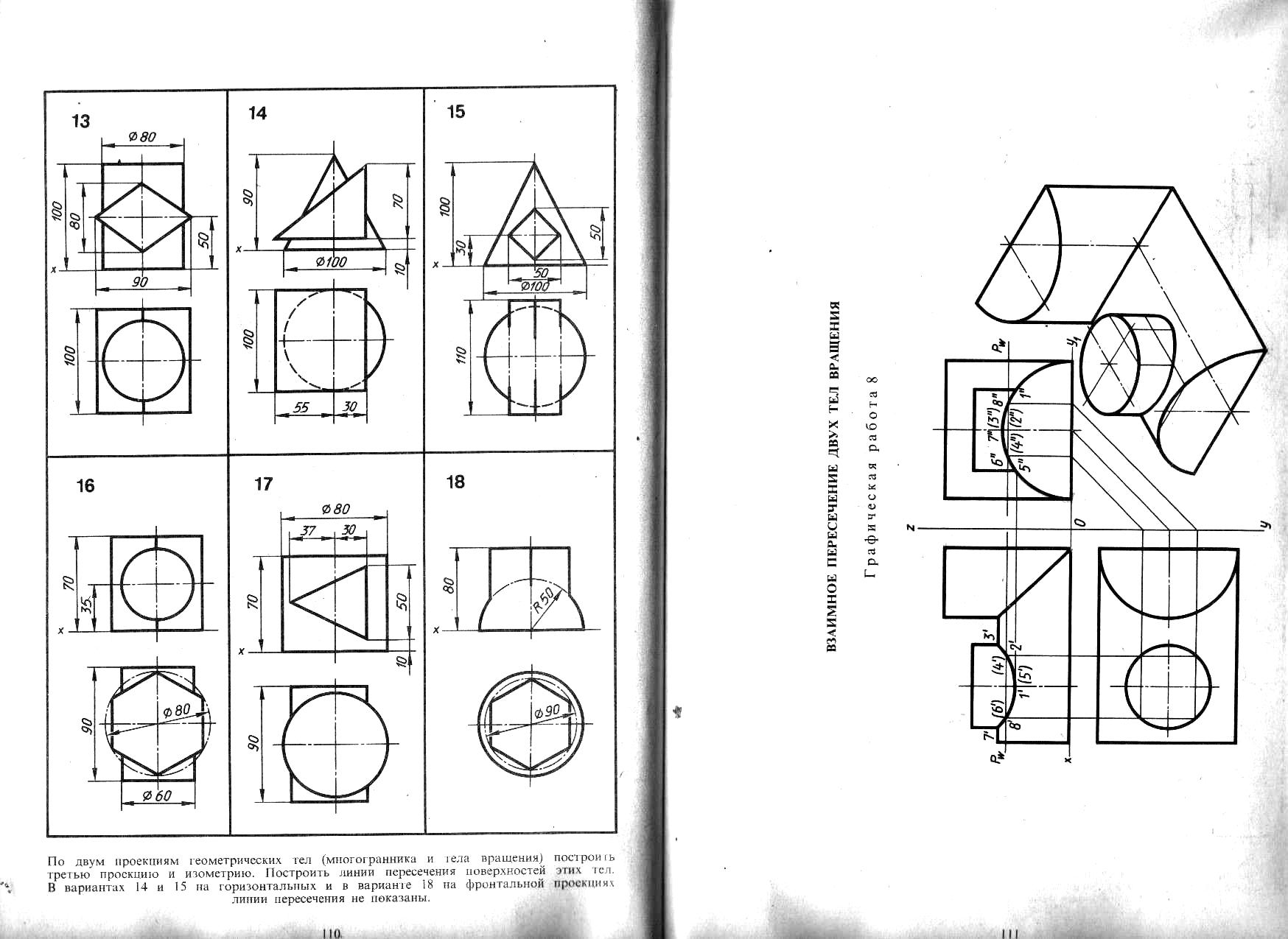
15. По двум проекциям геометрических тел (многогранника и тела вращения) построить третью проекцию. Пример построений показан на рисунке 13, исходные данные по вариантам смотреть в Приложении 2 Построить линию пересечения поверхностей этих тел. В вариантах 4, 7,14 ,15 и 11 линии пересечения на горизонтальной проекции не показаны, а в вариантах 8, 10 и 18 – на фронтальных проекциях.

Рисунок 13 – Пример построения
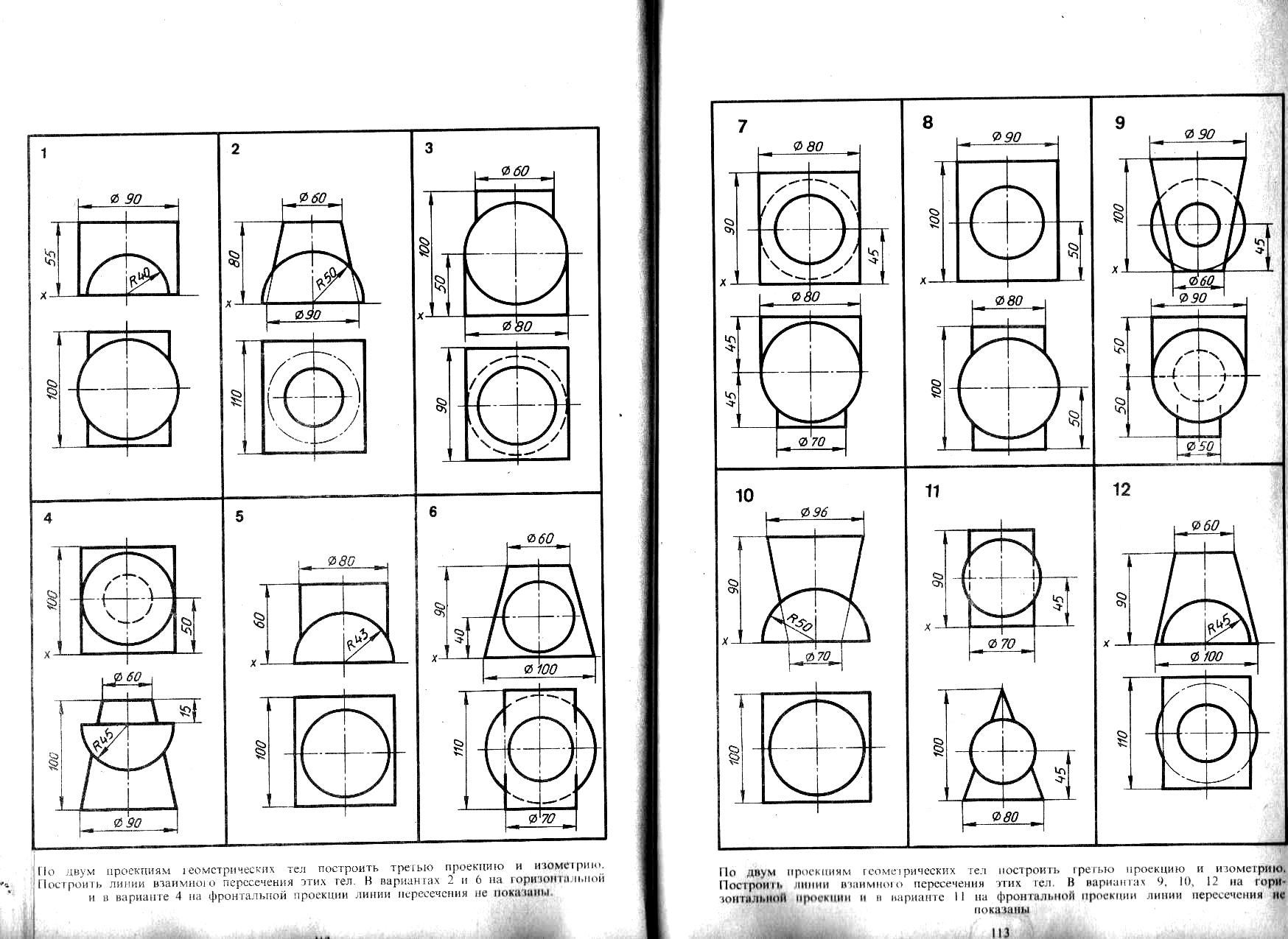
16. По двум проекциям геометрических тел построить третью проекцию. Построить линию взаимного пересечения этих тел. Пример построений показан на рисунке 14, исходные данные по вариантам смотреть в Приложении 3 В вариантах 2, 6, 9, 10, 12, 17, 18 на горизонтальной и в вариантах 4, 11,16 на фронтальной проекциях линии пересечения не заданы.
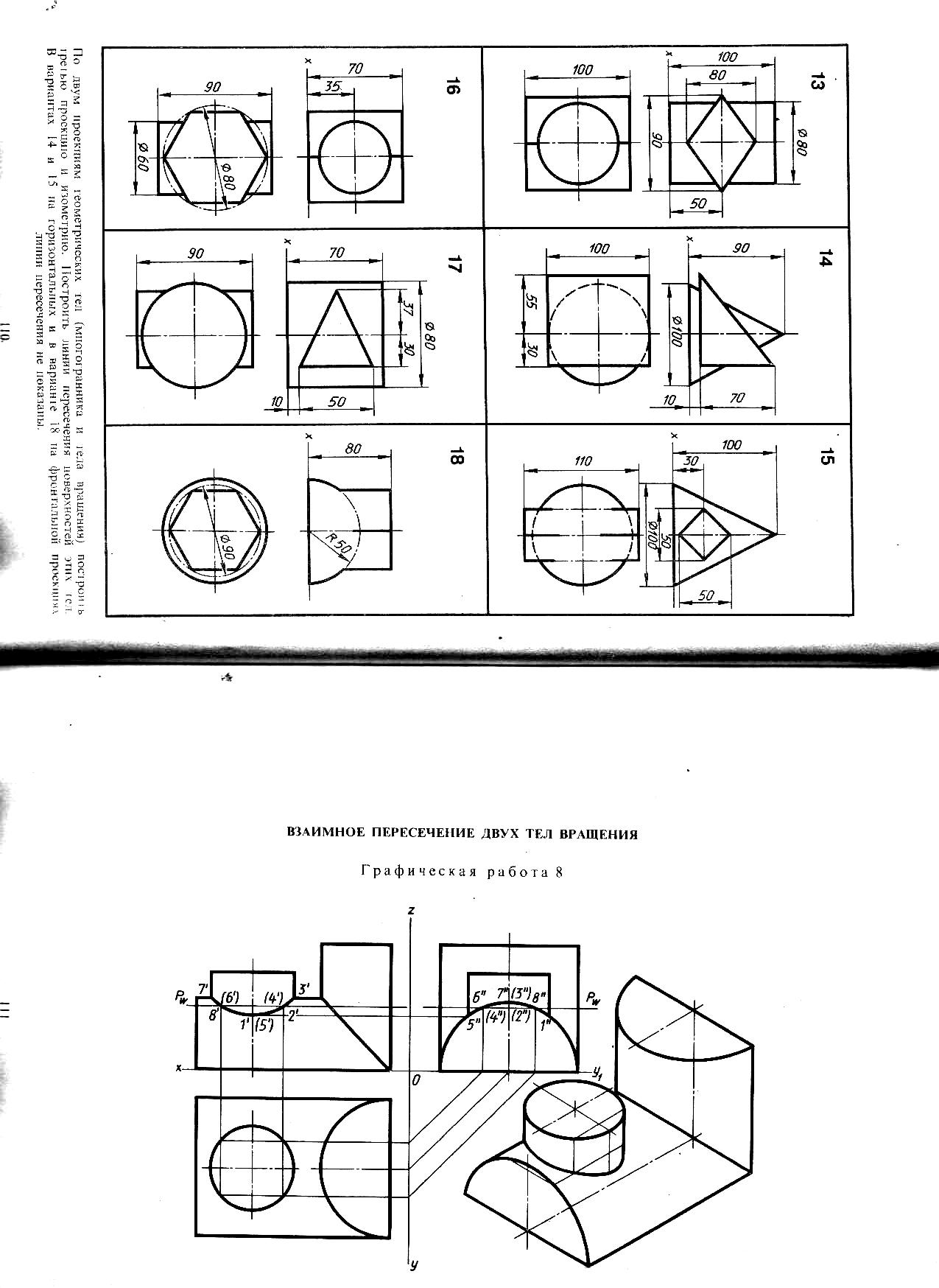 Рисунок
14 – Пример построения
Рисунок
14 – Пример построения
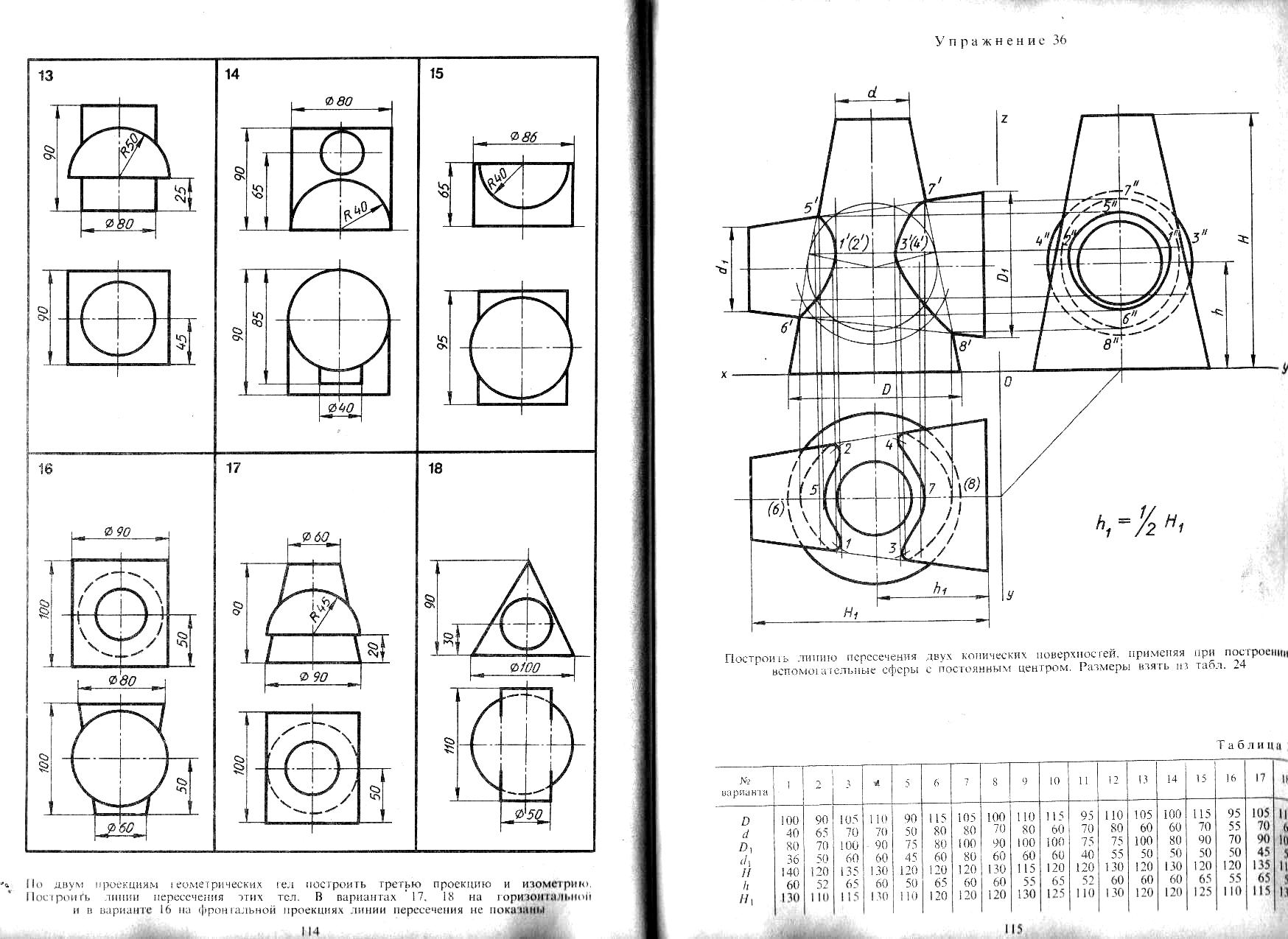
17. Построить линию пересечения двух конических поверхностей, применяя при построении вспомогательные сферы. Размеры взять из таблицы.
Таблица 13
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
D |
100 |
90 |
105 |
110 |
90 |
115 |
105 |
100 |
110 |
115 |
95 |
110 |
105 |
100 |
115 |
95 |
105 |
110 |
d |
40 |
65 |
70 |
70 |
50 |
80 |
80 |
70 |
80 |
60 |
70 |
80 |
60 |
60 |
70 |
55 |
70 |
60 |
D1 |
80 |
70 |
100 |
90 |
75 |
80 |
100 |
90 |
100 |
100 |
75 |
75 |
100 |
80 |
90 |
70 |
90 |
100 |
d1 |
36 |
50 |
60 |
60 |
45 |
60 |
80 |
60 |
60 |
60 |
40 |
55 |
50 |
50 |
50 |
50 |
45 |
50 |
H |
140 |
120 |
135 |
130 |
120 |
120 |
120 |
130 |
115 |
120 |
120 |
130 |
120 |
130 |
120 |
120 |
135 |
115 |
h |
60 |
52 |
65 |
60 |
50 |
65 |
60 |
60 |
55 |
65 |
52 |
60 |
60 |
60 |
65 |
55 |
65 |
55 |
H1 |
130 |
110 |
115 |
130 |
110 |
120 |
120 |
120 |
130 |
125 |
110 |
130 |
120 |
120 |
125 |
110 |
115 |
130 |
Пример построения приведен на рисунке 15.
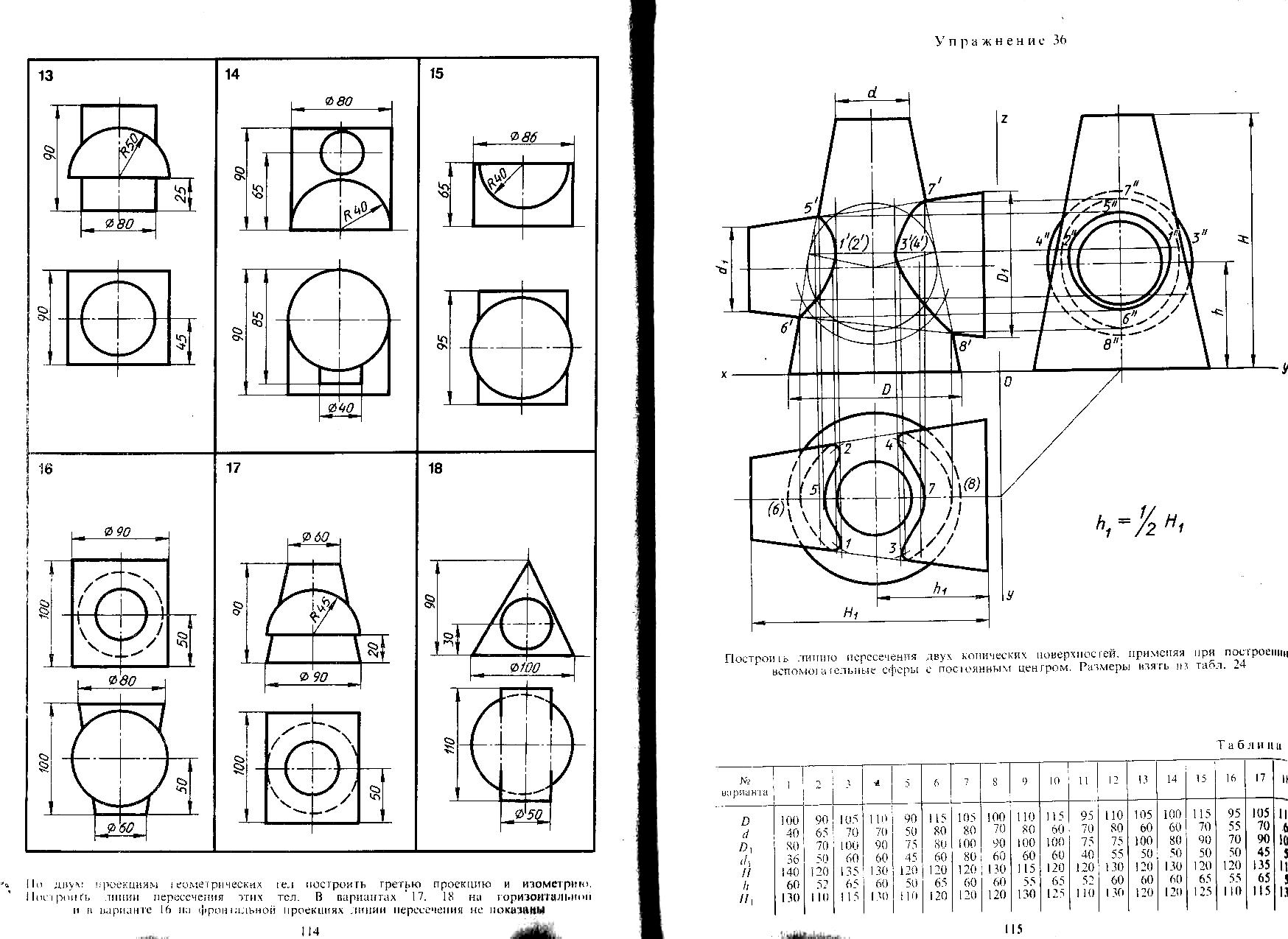
Рисунок 15 - Пример построения
П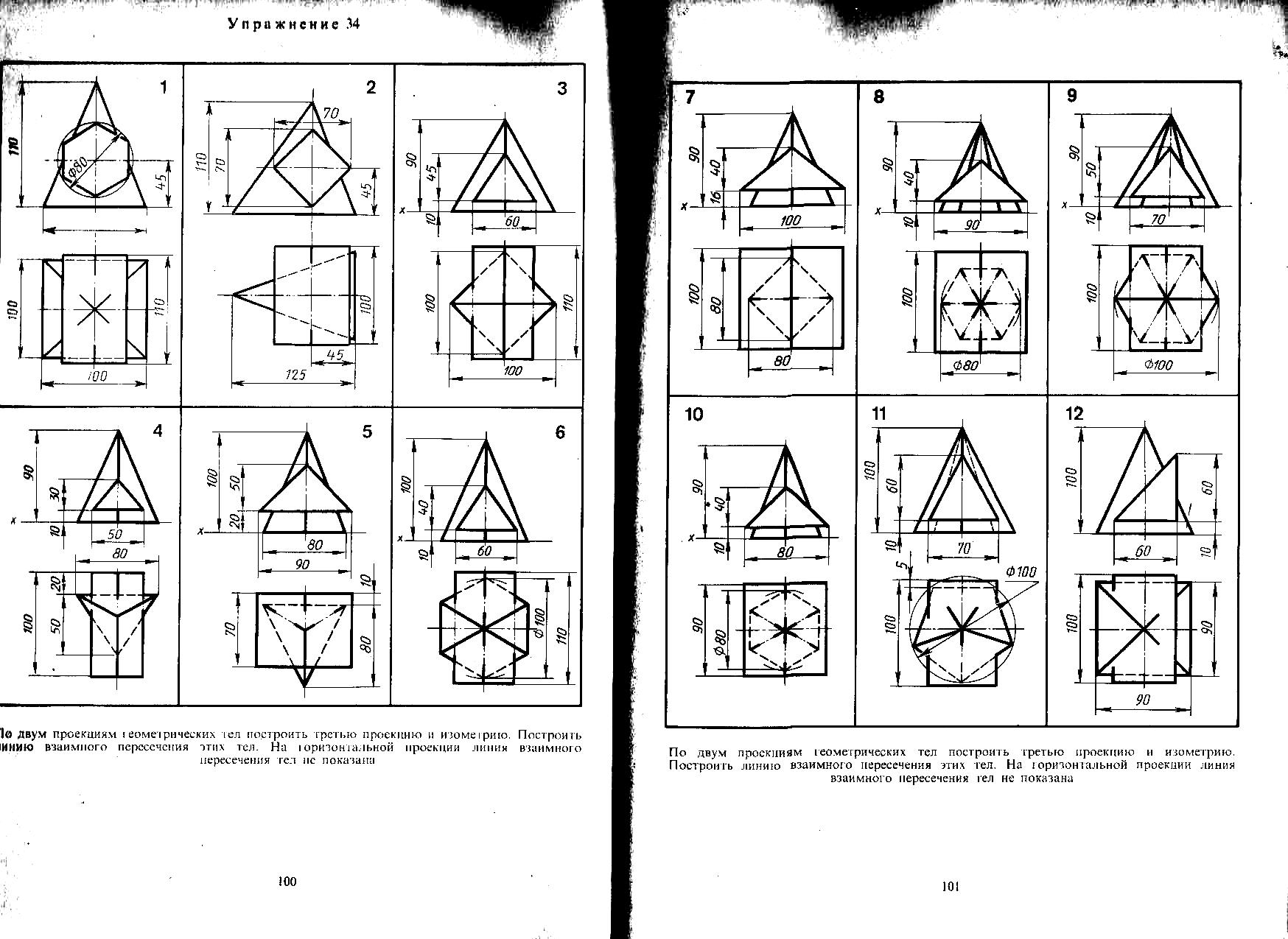 РИЛОЖЕНИЕ
1
РИЛОЖЕНИЕ
1
ПРИЛОЖЕНИЕ 1
ПРИЛОЖЕНИЕ 1
ПРИЛОЖЕНИЕ 2
ПРИЛОЖЕНИЕ 2
ПРИЛОЖЕНИЕ 2
ПРИЛОЖЕНИЕ 3
ПРИЛОЖЕНИЕ 3
ПРИЛОЖЕНИЕ 3
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1

