Итерационные соотношения
y Из прямоугольного треугольника, образованного 1ой касательной
,
0 a b x
- итерационное соотношение.
Итерационное соотношение требует расчёта производной. Обычно производную определяют численные методы. Аналитически можно уменьшить затраты на одну итерацию, если воспользоваться квазиньютоновским методом, предполагающим вычисление производной и использование.Это значение производной используем несколько раз.
Геометрическая интерпретация Ньютоновского метода.
y
Использовать более 3х раз одну касательную
не целесообразно т.к. начинается
существенно увеличиваться количество
итераций.
0 a b x
Параллельные линии.
Завершение
итерационного процесса: наиболее
эффективной метод по изменению знака
функции при добавлении
к аргументу
,
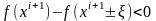где
заданная степень точности.
Метод Ньютона один их основных методов решения линейных уравнений.
Преимущества:
Высокая скорость сходимости(не вязно уменьшается пропорционально квадрату).
Малое число итераций.
Недостатки:
Высокая трудоёмкость расчёта одной итерации.
Жёсткие условия сходимости.
Один из наиболее применяемых методов.
Метод Ньютона – Рафсона.
Данный метод является развитием метода Ньютона для решения системы нелинейных алгебраических уравнений. Условия сходимости аналогично условиям сходимости, предъявляемым для одного уравнения. Отличия: 2ая производная рассматривается как по одной переменной так и по двум переменным.
Геометрическая
интерпретация метода аналогична методу
Ньютона
в n-переменном пространстве
и с n функциями.
…….
Итерационные соотношения получаем,
разложив функции
в
ряд Тейлора.
……………..
Перейдём к
матричной форме задания, выделив отдельно
матрицу производных, матрицу поправок
аргументов
и
матрицу значений функций.
(1)
i,(i+1) – номер итерации
-запись
номера итерации первой производной.
Последнее соотношение является приближённым, т.к. не учитывает результат разложения в ряд начиная со 2ой производной и выше.
Индекс i в обозначениях функции и аргумента указывает на номер итерации.
Если обозначить
матрицы:
,
где
-
соответствующие матрици.
Рассчитать
вектор аргументов на(ver)
итерации можно на основе соотношения
W-матрица Якоби(Якобиан)
Решение системы линейных уравнений (1) или (1’) относительно требует обращения матрицы, что составит значительную трудность.
Возможно уменьшение трудоёмкости за счёт:
Применения квазиньютоновского подхода.
Упрощенные методы расчёта Якобиана на(i+1) итерации по известному Якобиану на i-ой итерации и (i-1) итерации.
Смотреть самостоятельно блок-схему методы в Калабенове.
Метод Бройдена
Самостоятельно - книга.
Характеристики, рассчитывается на постоянном токе
Uвых Пр. Полученную характеристику в Micro CAPе в De Analise. Это однократный или многовариантный анализ? Ответ- многовариантный анализ.
0
Список характеристик.
V(R1) I(R2) I(R1)*U(R1) -на входе
I(1;2)? -на выходе
V(1;2) I(1) -на элементе
3*3=9 9*9=81
Т.е. всего уже 81 характеристики
Коэффициент передачи по напряжению, по току, по мощности:
12*12=144 характеристики.
Какие характеристика можем посмотреть!!
И на постоянном токе, в частотной области(характеристики) сопротивление проводимости. (лекции по ОТУ)! Все характеристики.