Метод статических описаний (метод Монте-Карло)

Назначение:

по известным статическим характеристикам внутренних параметров схемы(параметры: сопротивление резистора, ёмкость конденсатора, температурный коэффицент) статические характеристики(математическое ожидание или номинал, допуск, корреляция его, вид закона распределения) производим расчёт статических параметров выходной мощности.

Пример выходной характеристики: уровень сигнала на выходе; диапазон частот, частота среза

Статические параметры: гистограмма, математическое ожидание, дисперсия, вид закона распределения.

Условия применимости метода без ограничений на вид зависимости.

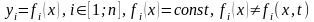
Замечание:

На практике(пакетах) вид закона распределения внутренних параметров обычно одинаков для совокупности параметров.

Ограничение:

Все виды функций распределения реализованных в пакетах

1. Вид закона распределения

2. Математическое ожидание(номинал

3. Допуск

4. Структура схемы, параметры элементов

Расчёт на основе метода Монте-Карло – многовариантный, количество испытаний(число расчётов в априорно до начала моделирования) и не апосториорно по повторяемости результатов с заданной степени точности.

N=200; M=1,873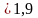

повторяемость в двух знаках.

N=200; M=1,861

Если полученная точность устраивает, количество исключений увеличивать не требуется, если не устраивает, то следует увеличивать N и процедуру поврторять, обычно в пакетах ограничено на:

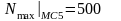
Алгоритм расчёта по методу Монте-Карло

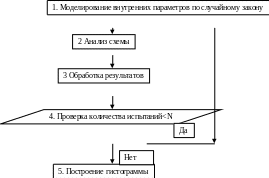
Преимущества:

а) возможность расчёта сложных схем с большим количеством корреляционных связей и без ограничений на вид зависимости выходной характеристики от внутренних параметров

б) высокая статическая достоверность результатов при правильном выборе количества испытаний

Недостатки:

а) необходимо знать статические сведения о внутренних параметрах в большем объёме по сравнению с другими методами

б) значительные вычислительные затраты порядка 5-10% требуют N порядка 500-1000 испытаний

Данный метод может быть реализован лишь на основе вычислительной техники. При статических испытаниях обычно решаются две задачи:

1. Прямая – по заданным отклонениям внутренних параметров определяется отклонения выходных характеристик 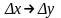. Данная задача решается достоверно с помощью нескольких операций (для проверки результатов).

2. Обратная – представляет практический интерес. В общем случае для большого количества элементов порядка 1000, данная задача решений не имеет( трудоёмкая)

Для ряда частных случаев, разработаны алгоритмы решения:

Пример: количество внутренних параметров, имеющих разброс менее 10:

а) для элементов задаём максимальный допуск

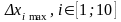
б) рассчитываем 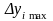, соответствует

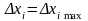
- определяем достоверность результата

- сравниваем

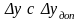
Если отклонение выходной характеристики не соответствует ТЗ( ), то

3. Определяем вляние внутренних параметров на выходную характеристику

Переходим в режим Stepping:

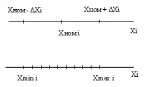
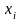- i-ый внутренний параметр

- номинальное значение

- допуск

Определяем и ;

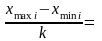
k – число интервалов <100

В результате многовариантного анализа получаем семейство выходных характеристик по истинным определяем отклонение :

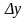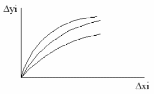
Итак, для каждого внутреннего параметра сопоставляя значения определяем внутренние параметры влияния которых на обходную характеристику наиболее. У этих параметров уменьшаем величину допуска и переходим к шагу 2. Процедуру завершаем, когда будет удовлетворять требованиям ТЗ.