Алгоритм Расчёта

Допустим, что условие, работоспособности в техническом задании задано в виде:

1)

Пример: уровень побочных гармоник или описание характеристики от заданного вида, тогда:

- максимальное значение i-го выходного параметра

- значение внутреннего параметра, соответствующему случаю и определённому по следующему соотношению:

2)

Пример: уровень напряжения, уровень мощности

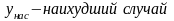
При рассмотренных соотношений должны выноситься условия:

1) ; sign - знак

2)

Оба эти условия выполняются на основе малых отклонений

Последовательность расчёта

1. рассчитываем знаки коффицента чувствительности для всех выходных параметров

2. находим значения внутренних параметров, соответствующих наихудшим случаям ( )

3. проводим однократный анализ схемы при соответствующих значениях внутренних параметров( )

Если для ряда i-ых значений выходного параметра требуется иной набор , то расчёт повторяем

«+» :

1. простота

2. небольшое количество расчётов

3. не требует знание вид закона распределения внутренних параметров

«-» :

1. полученные оценки являются завышенными

2. базируется на методе малых отклонений

3. требует расчётов знаков коэффицентов чувствительности

1. На практике знаки коэффицентов чувствительности могут быть определены через режим Stepping

2. Линейная выходная характеристика от внутреннего параметра также могут быть определена в режиме Stepping

Метод моментов

Метод получил такое наименование, т.к. исходными данными для расчёта являются моменты I и II рода для внутренних параметров +…… результат расчёта, моменты I и II рода(мат. Ожидание и дисперсия) для выходной характеристики.

Назначение метода:

Для расчёта математического ожидания и дисперсии выходной характеристики.

Условие применимости метода можем взять и рассчитать:

1. базируется на методе малых отклонений, следовательно зависимость откорнений выходной характеристики от отклонения внутренних параметров должна быть линейной

2. вид закона распределения отклонения внутренних параметров: нормальный, Гауссовский и т.д.

Исходные данные для расчёта

1. Математическое ожидание – отклонение внутреннего параметра от номинального значения

n – количество параметра

2. Дисперсия внутреннего параметра

3. Корреляционная матрица связи внутренних параметров. Отклонение внутреннего параметра по диагонали равно единице:

4. коэффицент пропорциональности между отклонением внутренних параметров коэффицентов пропорциональности является коэффицентом чувствительности (коэффицентом влияния)

Коэффицент влияния может быть представлен как:

а) ненормированный коэффицент чувствительности, есть размерность:

б) не можем сказать об интервалах измерения(изменение по знаку и величине)

Используется нормированный коэффицент чувствительности.

- нормировка(избавились от размерности и применили к номинальному значению)

На практике коэффиценты влияния могут быть определены с помощью(на основе) схемы технического моделирования в режиме Stepping:

Задаём отклонение Смотрим изменения в семействе выходных характеристик и определений:

1. линейность зависимости выходные характеристики от внутреннего параметра.

Для нелинейной характеристики – проблема выбора

1)

2) находим отношение

Сравниваем 2 значения между собой

Если

Замечание.

Если приближается к погрешности вычислений, то следует увеличить.

Расчётные соотношения.

Если существуют корреляционные связи между параметрами, то дисперсия выходной характеристики:

, где - корреляционная матрица

«+» :

1. имеем аналитические зависимости между исходными данными и результатами, что даёт возможность использовать данный метод как для решения прямой задачи и для решения обратной задачи

2. повторяемость результата( при условии, что коэффицент чувствительности задан)

3. невысокая трудоёмкость расчета

«-» :

1. приближённый алгоритм(алгоритм, предполагающий вычисление с некоторой погрешностью)

2. преобразует дополнительной проверки условия применимости

На практике это проверяется в режиме Stepping, по каждому внутреннему параметру, для каждой выходной характеристике. Данная проверка по трудоёмкости на порядок сложнее самого метода.

3. необходимо знать величины коэффицентов чувствительности

После расчёта моментов выходной характеристики, зная вид закона распределения, можем рассчитать статические параметры

Самостоятельно: пример расчёта.