Задача 6

Имеются данные по 8 субъектам Российской Федерации за январь - март 2007г. о денежных доходах и потребительских расходах на душу населения в среднем за месяц, которые приведены в таблице:

Номер субъекта РФ			1	2	3	4	5	6	7	8
Денежные доходы, тыс. руб.		1,98		1,75	1,59	1,58	1,86	2,35	1,28	1,5
Потребительские расходы, тыс. руб.		1,4		0,82	1,26	1,18	1,52	1,23	0,93	1,1

Для необходимых промежуточных расчетов предлагается воспользоваться следующей таблицей данных.

	1	2	3	4	5	6	7	8	Сумма
x	1,98	1,75	1,59	1,58	1,86	2,35	1,28	1,5	13,89
y	1,4	0,82	1,26	1,18	1,52	1,23	0,93	1,1	9,44
квадрат x	3,9204	3,0625	2,5281	2,4964	3,4596	5,5225	1,6384	2,25	24,878
произведение xy	2,772	1,435	2,0034	1,8644	2,8272	2,8905	1,1904	1,65	16,633
квадрат y	1,96	0,6724	1,5876	1,3924	2,3104	1,5129	0,8649	1,21	11,511

Квантиль распределения Стьюдента при уровне значимости 0,1 равняется 1,943.

На основе имеющихся данных требуется:

1. Построить поле рассеяния наблюдаемых значений показателей и на основе его визуального наблюдения выдвинуть гипотезу о виде статистической зависимости потребительских расходов y от денежных доходов x; записать эту гипотезу в виде математической модели.

2. Используя метод наименьших квадратов, найти точечные оценки неизвестных параметров модели, записать найденное уравнение регрессии и построить график функции регрессии.

3. Найти коэффициент парной корреляции между денежными доходами и потребительскими расходами.

4. Найти точечный и интервальный прогноз среднемесячных потребительских расходов в 8-ом субъекте РФ в будущем периоде при уровне значимости равном 0,1 предполагая, что среднемесячные денежные доходы в этом субъекте РФ увеличатся на 30 %.

5. Привести содержательную интерпретацию полученных результатов.

Решение:

1. Построим поле рассеяния:

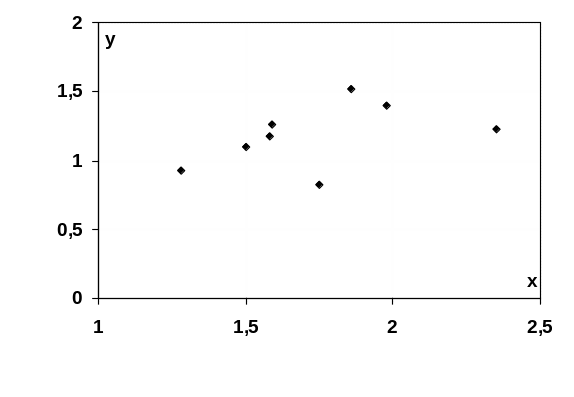
На основе визуального наблюдения поля рассеяния можно выдвинуть гипотезу о линейной зависимости потребительских расходов y от денежных доходов x, которую в математическом виде можно записать как .

2. В соответствии с методом наименьших квадратов найти оценки линейного уравнения регрессии можно найти так:

;

,

Получили линейное уравнение регрессии:

Вычислим значения для заданных значений х:

х	1,98	1,75	1,59	1,58	1,86	2,35	1,28	1,5
у	1,4	0,82	1,26	1,18	1,52	1,23	0,93	1,1
	1,386	1,091	1,253	1,224	1,354	1,423	0,998	1,192

3. Коэффициент парной корреляции вычислим по формуле:

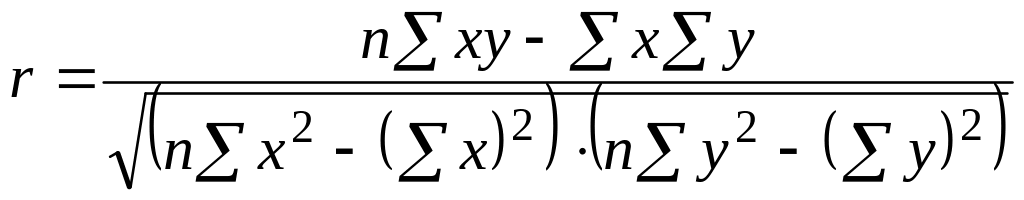
4. При увеличении среднемесячного денежного дохода в 8-м субъекте РФ на 30% его значение будет равно . Подставив это значение в полученное уравнение линейной регрессии, получим точечный прогноз среднемесячных потребительских расходов:

Формула для интервального прогноза:

,

где - значение квантили распределения Стьюдента,

, ,

Для удобства вычисления занесем в таблицу рассчитанные значения:

х	1,98	1,75	1,59	1,58	1,86	2,35	1,28	1,5
у	1,4	0,82	1,26	1,18	1,52	1,23	0,93	1,1
	1,386	1,091	1,253	1,224	1,354	1,423	0,998	1,192
	0,244	0,014	-0,146	-0,156	0,124	0,614	-0,456	-0,236
	0,059	0,000	0,000	0,024	0,015	0,377	0,208	0,056	0,740
	0,14	-0,36	0,13	0,05	0,30	-0,15	-0,10	0,00
	0,020	0,133	0,016	0,002	0,090	0,021	0,011	0,000	0,294

,

,

Интервальный прогноз:

5. В полученном уравнении линейной регрессии значение коэффициента показывает, что при увеличении доходов на одну тысячу рублей среднемесячные потребительские расходы населения вырастут на 0,319 тыс. руб. Интерпретация свободного члена этого уравнения не имеет экономического смысла, так как характеризует уровень потребительских расходов при нулевых доходах. Полученное значение коэффициента корреляции говорит о заметной прямой линейной связи между денежными доходами и потребительскими расходами.