Задача 4
Фирма при производстве
продукции использует два вида ресурсов:
рабочую силу (L, тыс. чел.-час.) и оборудование
(K, тыс. ст.-час.). Производственная функция
(ПФ) фирмы, построенная путем обработки
статистических данных, имеет вид:
,
где Y - объем выпуска продукции (ед.).
Требуется:
Построить графики ПФ при фиксированном значении одной из переменных: а) K=108, б) L = 36.
Найти уравнения изоквант ПФ и построить их графики для Y1=133, Y2=200, Y3=267.
Пусть известны объем выпуска продукции Y=200 и наличные трудовые ресурсы L=36 в базовом периоде. Определить потребность в оборудовании в плановом периоде при увеличении объема выпуска продукции на 10%, если возможность увеличения трудовых ресурсов составляет не более 5%.
Рабочая сила нанимается по контракту с почасовой оплатой труда 560 (ден.ед./тыс. чел.-час), оборудование берется в аренду с суммарными затратами 80 (ден.ед./тыс. ст.-час). Объем капитала, который фирма может затратить на рабочую силу и оборудование, составляет 32000 (ден. ед.). Построить математическую модель задачи оптимизации выпуска продукции, считая, что производственная функция задана на множестве K >=0, L >= 0, и найти графическим методом ее решение. Определить предельную норму технологического замещения оборудования рабочей силой и предельную эффективность финансовых ресурсов в точке оптимума.
Решение:
1. При K=108 ПФ примет
вид:
,
ее график:
L
Y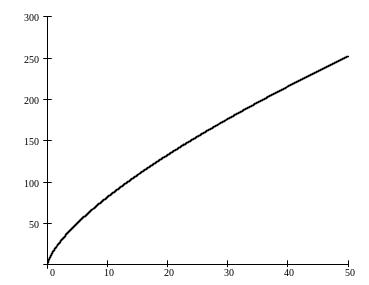
б) При L = 36 ПФ примет
вид:
,
ее график
Y
K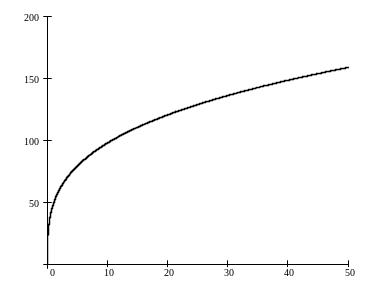
2. Найдем уравнения изоквант, то есть зависимость K(L), предполагая, что Y=const:
Построим графики изоквант при Y1=133, Y2=200, Y3=267:
Y=267
Y=200
Y=133
3. Объем выпуска продукции Y=200 при наличных трудовых ресурсах L=36 в базовом периоде обеспечивает количество оборудования, равное
тыс. ст.-час.
Если объем трудовых ресурсов, используемых в производстве, не изменится, то потребность в оборудовании в плановом периоде составит:
тыс. ст.-час.
Если объем трудовых ресурсов, используемых в производстве, вырастет на 5%, то потребность в оборудовании в плановом периоде составит:
тыс. ст.-час.
То есть при объеме
трудовых ресурсов
потребность в оборудовании в плановом
периоде составит некоторую величину
,
определяемую соотношением
4. Математическая модель задачи оптимизации выпуска продукции:
Прямая, соответствующая
ограничению, будет иметь вид
,
значит, областью допустимых решений
будет внутренняя часть треугольника
ОАВ, ограниченная прямыми
,
,
.
Изобразим на графике одну из изоквант
и область допустимых решений:
А
В
O
K
L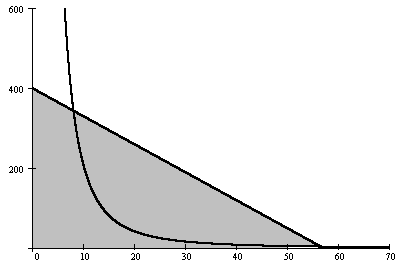
Видим, что
максимального значения ПФ будет достигать
на отрезке АВ. На этом отрезке функция
будет иметь вид:
.
Чтобы найти точку экстремума,
продифференцируем полученную функцию:
Найдем критические точки. Производная не существует в нуле знаменателя:
Производная равна нулю в точке:
Первые 2 критические точки – концы отрезка АВ. Во всех трех критических точках найдем значения функции:
,
,
Таким образом,
оптимальным решением будет
,
,
при этом ПФ будет равна
.
Предельная норма замещения оборудования рабочей силой:
Предельная эффективность финансовых ресурсов:
