1 Практическое занятие № 1 (оформить в тетради)

РАСЧЕТ ПОРИСТОСТИ, ПРОНИЦАЕМОСТИ И УДЕЛЬНОЙ ПОВЕРХНОСТИ ГОРНОЙ ПОРОДЫ

Под пористостью горной породы понимают наличие в ней пустот (пор).

Коэффициентом полной (или абсолютной) пористости m_п называется отношение суммарного объема пор V_пор в образце породы к видимому его объему V_обр:

(1.1)

Измеряется коэффициент пористости в долях единицы или в процентах объема породы.

Структура порового пространства пород зависит от гранулометри-ческого состава частиц, их формы, химического состава пород, происхождения пор, а также от соотношения количества больших и малых пор.

В большой степени свойства пористых сред зависят от размеров поровых каналов, диаметр которых может изменяться от 0,0002 мм (и менее) до 0,5 мм (и более). Поэтому, при существующих в естественных условиях перепадах давлений, не во всех пустотах жидкости и газы находятся в движении.

Наряду с коэффициентом полной пористости существует понятие открытой пористости.

Коэффициентом открытой пористости m_о называется отношение объема открытых, сообщающихся пор, к объему образца:

(1.2)

Из определения понятия коэффициента полной пористости вытекают следующие соотношения:

(1.3)

где V_пор, V_обр и V_зер – соответственно объемы пор, образца и зерен.

Пористость пород нефтяных и газовых пластов может изменяться в широких пределах – от нескольких процентов до 55%. В большинстве случаев она составляет 15-20%.

Проницаемость – фильтрационный параметр горной породы, характеризующий ее способность пропускать к забоям скважин жидкости и газы.

В процессе разработки нефтяных и газовых месторождений встречаются различные виды фильтрации в пористой среде жидкостей и газов или их смесей – совместное движение нефти, воды и газа, воды и нефти, нефти и газа или только нефти либо газа. При этом проницаемость одной и той же пористой среды в зависимости от количественного и качественного состава фаз будет различной. Поэтому для характерис-тики проницаемости пород нефтегазосодержащих пластов введены понятия абсолютной, эффективной (фазовой) и относительной проницаемостей.

Под абсолютной принято понимать проницаемость пористой среды, которая определена при наличии в ней лишь одной фазы, химически инертной по отношению к породе. Абсолютная проницаемость – свойство породы, и она не зависит от свойств фильтрующейся жидкости или газа и перепада давления, если нет взаимодействия флюидов с породой. На практике жидкости часто взаимодействуют с породой (глинистые частицы разбухают в воде, смолы забивают поры). Поэтому для оценки абсолютной проницаемости обычно используется воздух или газ, так как установлено, что при движении жидкостей в пористой среде на ее проницаемость влияют их физи­ко-химические свойства.

Фазовой называется проницаемость пород для данного газа или жидкости при наличии или движении в порах многофазных систем. Значение ее зависит не только от физических свойств пород, но и от степени насыщенности порового пространства жидкостями или газом и их физико-химических свойств.

Относительной проницаемостью пористой среды называется отношение фазовой проницаемости этой среды для данной фазы к абсолютной проницаемости.

Для оценки проницаемости горных пород обычно пользуются линейным законом фильтрации Дарси:

υ = = (1.4)

где υ – скорость линейной фильтрации, м/с;

Q – объемный расход жидкости через породу в единицу времени, м³/с;

F – площадь фильтрации, м²;

μ – динамическая вязкость жидкости, Па∙с;

Δр – перепад давлений (Δр = р₁- р₂), Па;

ΔL – длина пористой среды, м;

k – коэффициент пропорциональности, который называют коэффициентом проницаемости.

Из формулы (1.4) следует, что коэффициент проницаемости равен:

k = (1.5)

Используя Международную систему единиц (СИ), из закона Дарси следует, что коэффициент проницаемости имеет размерность площади – м². Физический смысл размерности k (площадь) заключается в том, что проницаемость характеризует площадь сечения каналов пористой среды, по которым в основном происходит фильтрация.

В нефтегазопромысловой практике проницаемость измеряется в мкм²:

1 мкм² = 10^-12 м².

Внесистемной единицей измерения проницаемости является дарси:

1 Д = 1,02 ∙ 10^-12 м² = 1,02 мкм².

Реальные пласты обладают следующими проницаемостями:

1. k > 1 мкм² – высокая проницаемость;

2. 0,3 мкм² < k < 1 мкм² – хорошая проницаемость;

3. k < 0,3 мкм² – низкая проницаемость.

При изучении общей картины движения жидкостей в пористых средах (например, изменения давления в пласте или определения дебита залежи) пользуются понятием скорости фильтрации.

Скоростью фильтрации υ называется отношение объемного расхода жидкости Q (м³/с) к площади поперечного сечения пласта F (м²), нормального (перпендикулярного) к на­правлению движения жидкости:

. (1.6)

Скорость фильтрации представляет собой фиктивную скорость, с кото­рой двигалась бы жидкость, если бы пористая среда отсутствовала (m = 1).

При изучении микродвижения жидкости в пористой среде пользуются понятием средней истинной скорости движения.

Средняя скорость движения жидкости w (или средняя истинная скорость движения частиц жидкости) равна отношению объемного расхода жидко­сти Q (м³/с) к площади просветов F_пор (м²) (живому сечению потока) (рисунок 1.1):

w = (1.7)

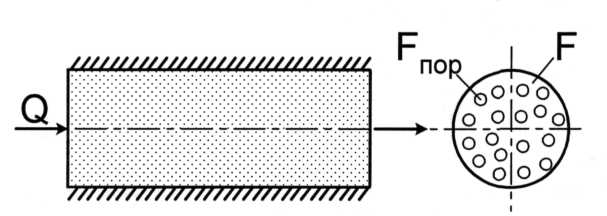
Рисунок 1.1 – Схема фильтрации жидкости через пористую среду:

F – суммарная площадь пустот и зерен в сечении пористой среды;

F_ПОР – суммарная площадь сечений поровых каналов, по которым идет фильтрация (живое сечение потока).

Скорость фильтрации и средняя скорость движения связаны соотноше­нием:

w = υ/m. (1.8)

При фильтрации в пористой среде только газовой фазы для расчета проницаемости пород по газу в формулу (1.5) следует подставлять средний расход газа в условиях образца:

k = (1.9)

где – объемный расход газа, приведенный к среднему давлению и средней температуре газа в образце, м³/с.

Необходимость использования среднего расхода газа в этом случае объясняется непостоянством его объемного расхода при уменьшении давления по длине образца.

Среднее давление по длине керна

(1.10)

где p₁ и p₂ – давление газа на входе в образец и на выходе из него соответственно, Па.

Полагая, что процесс расширения газа при фильтрации через образец происходит изотермически по законам идеального газа, используя закон Бойля-Мариотта, получим:

(1.11)

где Q_о – расход газа при атмосферном давлении р_о (p_о = 0,1 МПа).

Тогда формула для определения проницаемости пород по газу запишется в следующем виде:

k = (1.12)

Удельная поверхность горных пород – это суммарная поверхность частиц или поровых каналов в единице объёма образца. От её величины зависят проницаемость, адсорбционная способность, содержание остаточной воды в породе.

В связи с тем, что диаметры пор изменяются от десятков и сотен микрометров до размеров молекул, очень сложно точно определить величину удельной поверхности пород.

Упрощенной моделью пористой среды является модель фиктивного грунта. Фиктивный грунт состоит из шариков одного диаметра, уложенных определенным образом. При схеме, показанной на рисунке 1.2. а, пористость будет наибольшая. Когда же в проходном сечении образуются криволинейные треугольники (рисунок 1.2. б), пористость будет соответственно меньше.

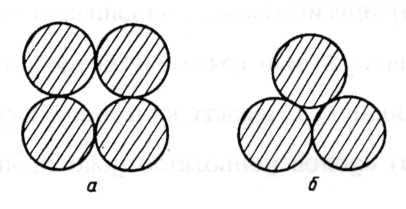
Рисунок 1.2 – Схемы укладки сферических зерен:

а – наибольшая пористость; б – наименьшая пористость.

Установлено, что если бы все частицы имели шарообразную форму (фиктивный грунт), то поверхность всех частиц в 1 м³ породы составила бы

S_УД = (1.13)

где S_уд – удельная поверхность, м²/м³;

m – коэффициент пористости, дол. ед.;

d – диаметр час­тиц, м.

Приближенно удельная поверхность S_уд определяется расчетным путем в зависимости от проницаемости и пористости по формуле:

S_УД = (1.14)

где k – проницаемость, м²;

m – коэффициент пористости, доли ед.;

S_уд – удельная поверхность, м²/м³.

Если выразить проницаемость в мкм², то удельную поверхность можно определить по формуле:

S_УД = (1.15)

где S_уд – удельная поверхность, м²/м³;

m – коэффициент пористости, доли ед.;

k – коэффициент проницаемости (в формулу подставляется в мкм²).

Зная удельную поверхность породы, и считая, что частицы имеют сферическую форму, можно определить число частиц в 1 м³ грунта:

N = (1.16)

где S_сферы = 4π∙r² = π∙d². – площадь сферической поверхности частицы, м²;

d – диаметр частицы, м.

Задачи

Задача 1.1. Определить коэффициент полной пористости m_П образца породы, если известны объем образца V_о, а также объём зерен в образце V_з. Исходные данные для расчётов представлены в таблице 1.1.

Таблица 1.1 – Исходные данные для расчёта коэффициента пористости

Номер варианта	Vо, см3	Vз, см3	Номер варианта	Vо, см3	Vз, см3
1	2	3	4	5	6
1	2,42	2,02	16	2,82	2,47
2	3,58	3,25	17	3,00	2,57
3	4,50	3,00	18	2,62	2,15
4	3,80	2,50	19	3,06	2,51
5	5,04	4,66	20	2,75	2,11
6	3,60	3,10	21	3,44	2,47
7	2,86	2,08	22	4,12	2,87
8	4,06	3,30	23	2,35	1,84
9	4,76	4,00	24	3,18	2,77
10	3,20	2,82	25	4,00	2,92
11	2,50	2,04	26	5,80	4,37
12	3,68	2,92	27	2,95	2,57
13	2,88	2,16	28	3,36	2,82
14	3,54	2,80	29	4,28	3,14
15	5,00	3,86	30	3,75	2,64

Задача 1.2. Определить коэффициент абсолютной проницаемости породы путем пропускания воздуха через образец, если длина образца составляет l, площадь его поперечного сечения F, давление перед образцом и за ним соответственно р₁ и р₂. Вязкость воздуха (в условиях опыта) равна μ; объем воздуха (при атмосферном давлении), прошедшего через образец за время t составил V_в. Исходные данные для расчетов представлены в таблице 1.2.

Таблица 1.2 – Исходные данные для расчёта коэффициента проницаемости

№ варианта	l, см	F, см2	р1, МПа	р2, МПа	μ, мПа∙с	t, с	Vв, см3
1	2	3	4	5	6	7	8
1	2,8	5,1	0,13	0,10	0,018	180	360
2	3,0	5,8	0,15	0,11	0,010	150	300
3	4,2	5,2	0,18	0,12	0,015	120	280
4	2,6	5,0	0,13	0,10	0,020	180	340
5	5,3	5,1	0,15	0,11	0,025	150	280
6	4,0	5,2	0,18	0,12	0,019	120	310
7	5,0	5,8	0,13	0,10	0,021	180	360
8	3,8	5,0	0,15	0,11	0,032	150	300
9	4,4	5,6	0,18	0,12	0,022	120	280
10	3,2	5,2	0,13	0,10	0,027	180	340
11	4,6	5,8	0,15	0,11	0,017	150	310
12	3,4	5,0	0,18	0,12	0,030	120	280
13	4,8	5,1	0,13	0,10	0,028	180	360
14	3,6	5,2	0,15	0,11	0,016	150	300
15	2,9	5,8	0,18	0,12	0,024	120	280
16	2,7	5,2	0,15	0,11	0,032	180	310
17	3,0	5,8	0,18	0,12	0,022	150	360
18	4,2	5,2	0,13	0,10	0,027	120	300
19	2,6	5,1	0,15	0,11	0,017	180	280
20	5,3	5,0	0,18	0,12	0,030	150	340
21	3,7	5,8	0,15	0,10	0,018	120	310
22	4,5	5,2	0,18	0,11	0,010	180	280
23	2,7	5,0	0,13	0,12	0,015	150	360
24	5,1	5,1	0,15	0,10	0,020	120	300
25	4,2	5,2	0,18	0,11	0,025	180	280
26	5,2	5,8	0,13	0,12	0,019	150	340
27	4,8	5,0	0,15	0,10	0,021	120	310
28	5,6	5,1	0,18	0,11	0,018	180	280
29	3,8	5,3	0,13	0,12	0,010	150	360
30	4,5	5,6	0,15	0,10	0,015	120	320

Задача 1.3. Определить коэффициент пористости образца горной породы, зная скорость движения жидкости через образец w (определение проводилось при помощи индикатора), коэффициент проницаемости k, вязкость жидкости μ и разность давлений Δр при длине образца l. Исходные данные для расчетов представлены в таблице 1.3.

Таблица 1.3 – Исходные данные для расчёта коэффициента пористости

№ варианта	w, см/с	k, Д	μ, мПа∙с	Δр, кгс/см2	l, см
1	2	3	4	5	6
1	0,03	0,2	4,0	2,00	15
2	0,05	0,3	1,0	0,40	20
3	0,04	0,5	1,5	0,50	18
4	0,06	0,4	2,0	0,68	16
5	0,03	0,7	2,5	0,82	14
6	0,05	0,5	3,0	0,95	12
7	0,04	0,6	3,5	1,09	10
8	0,06	0,3	4,0	1,22	8
9	0,04	0,4	4,5	1,36	6
10	0,05	0,2	5,0	1,50	4
11	0,04	0,3	5,5	1,63	6
12	0,06	0,7	5,0	1,77	8
13	0,03	0,3	4,5	1,63	10
14	0,05	0,4	4,0	1,50	12
15	0,04	0,7	3,5	1,36	14
16	0,06	0,2	2,0	1,06	20
17	0,03	0,5	3,0	1,32	16
18	0,05	0,4	3,5	1,54	14
19	0,04	0,7	4,0	1,61	12
20	0,06	0,2	4,5	2,00	10
21	0,03	0,4	3,0	0,40	8
22	0,05	0,5	5,5	0,50	6
23	0,04	0,4	5,3	0,68	4
24	0,06	0,7	4,2	0,82	6
25	0,03	0,2	1,8	0,95	8
26	0,05	0,4	1,5	2,10	10
27	0,04	0,5	2,0	1,40	12
28	0,06	0,3	2,5	0,50	14
29	0,03	0,7	5,2	1,68	16
30	0,04	0,6	3,2	0,82	18

Задача 1.4. Определить удельную поверхность песка (поверхности песчинок, заключенных в 1 м³ песчаного пласта), пористость которого составляет m и эффективный диаметр песчинок (фиктивного грунта) d_э. Найти также число частиц N в единице объема пласта, принимая их форму сферической. Исходные данные для расчетов представлены в таблице 1.4.

Таблица 1.4 – Исходные данные для расчёта удельной поверхности песка

Номер варианта	m, %	dэ, мм	Номер варианта	m, %	dэ, мм
1	2	3	4	5	6
1	25	0,20	16	27	0,27
2	19	0,14	17	16	0,13
3	28	0,33	18	20	0,19
4	31	0,40	19	18	0,26
5	33	0,21	20	24	0,18
6	27	0,38	21	32	0,30
7	16	0,29	22	15	0,14
8	20	0,35	23	26	0,33
9	18	0,22	24	23	0,40
10	24	0,30	25	29	0,31
11	32	0,37	26	25	0,38
12	15	0,23	27	19	0,29
13	26	0,19	28	28	0,15
14	23	0,26	29	31	0,22
15	29	0,18	30	33	0,30

Задача 1.5. Определить удельную поверхность слабосцементи-рованного песчаника, если известны его проницаемость k и пористость m. Расчет провести по двум формулам: по формуле (1.14) и по формуле (1.15). Исходные данные для расчетов представлены в таблице 1.5.

Таблица 1.5 – Исходные данные для расчёта удельной поверхности слабосцементированного песчаника

№ варианта	k, мкм2	m, %	№ варианта	k, мкм2	m, %
1	2	3	4	5	6
1	2,5	23	16	1,9	21
2	1,7	18	17	3,6	28
3	3,0	30	18	2,4	15
4	2,8	24	19	1,8	20
5	1,9	16	20	2,2	31
6	3,4	29	21	2,5	16

Продолжение таблицы 1.5

1	2	3	4	5	6
7	1,2	14	22	1,6	24
8	2,2	25	23	2,0	18
9	1,8	19	24	1,7	26
10	3,5	28	25	3,0	22
11	1,6	17	26	2,8	23
12	1,4	20	27	1,9	30
13	2,0	22	28	2,3	17
14	2,3	26	29	3,2	29
15	3,9	32	30	1,7	19

2 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2 (оформить как контрольную работу и зарегистрировать в деканате Заочного факультета)

РАСЧЁТ ОСНОВНЫХ ПАРАМЕТРОВ, ХАРАКТЕРИЗУЮЩИХ СВОЙСТВА ПЛАСТОВЫХ ЖИДКОСТЕЙ И ГАЗОВ

2.1 Расчёт молекулярной массы и плотности газа

Одним из важных параметров газа является его молекулярная масса, которая определяется путем суммирования масс атомов, входящих в молекулу.

Молекулярная масса углеводородного газа, представляющего собою смесь компонентов, при известном объёмном составе, рассчитывается по формуле:

(2.1)

где y_i – объёмная доля i- го компонента в газовой смеси;

M_i – молекулярная масса i- го компонента;

n – число компонентов в смеси газов.

Под плотностью углеводородного газа понимают его массу, заклю-ченную в 1 м³ при определенных условиях (нормальных или стандартных), в системе СИ измеряется в кг/м³.

_г = m/V. (2.2)

Под нормальными условиями понимают условия, при которых давление Р = 0,1 МПа, а температура Т = 273 К (0С); под стандартными условиями – Р = 0,1 МПа, Т = 293 К (20С).

Для всех газов объем 1 киломоля постоянен и равен при нормальных условиях – 22,41 м³, при стандартных условиях – 24,05 м³. Зная молекулярную массу газа, плотность газа при нормальных условиях можно вычислить по формуле:

(2.3)

при стандартных условиях – по формуле:

(2.4)

На практике часто пользуются относительной плотностью газа, равной отношению плотности газа к плотности воздуха при определенных условиях:

(2.5)

При расчетах следует помнить, что плотность воздуха при нормальных условиях составляет _в^н.у. = 1,293 кг/м³, при стандартных _в^ст.у. = 1,205 кг/м³.

Зная молекулярную массу газа М_Г, относительную плотность газа можно рассчитать по формуле:

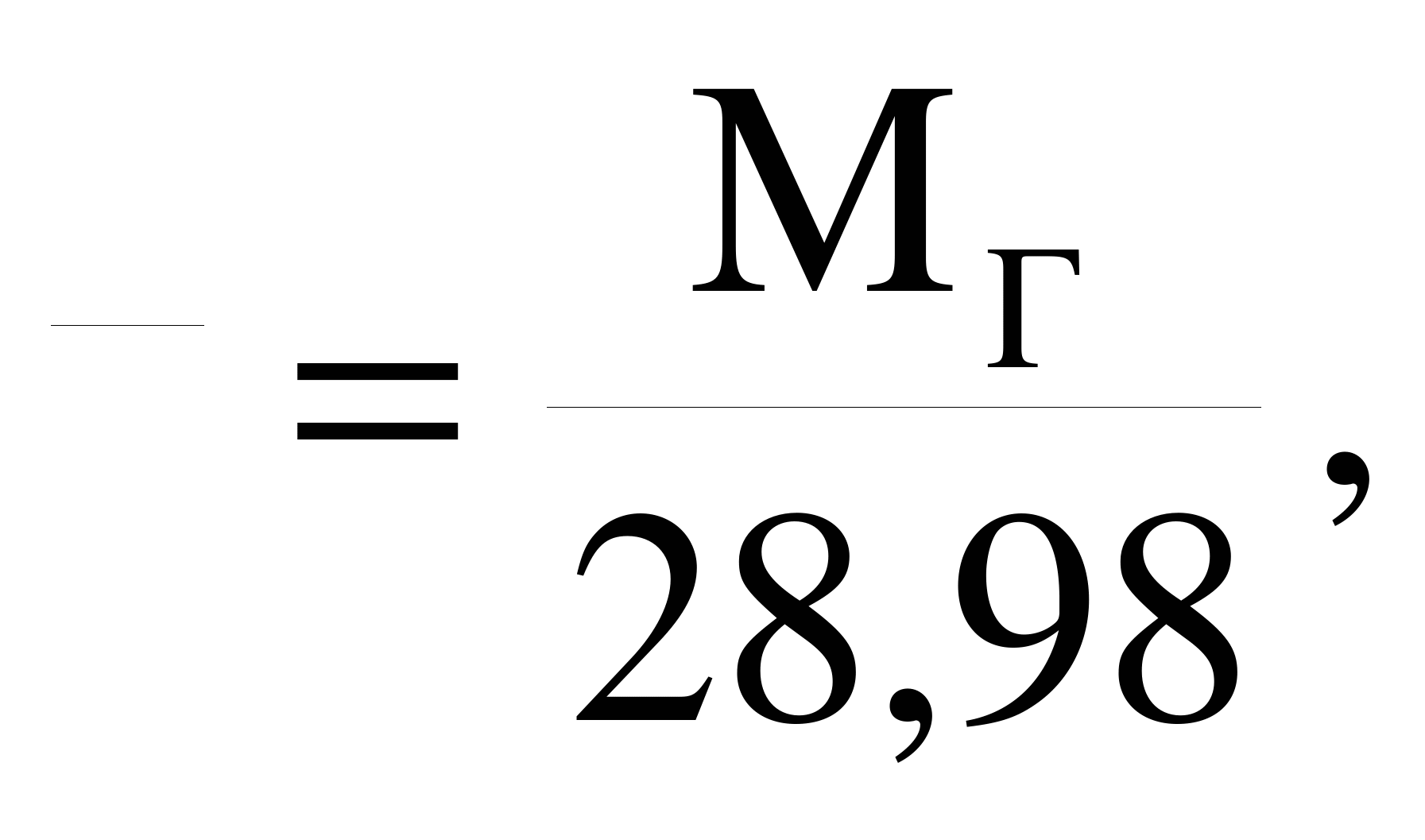(2.6)

где 28,98 – молекулярная масса воздуха.

Задача 2.1. Даны составы газов типичных газовых, газоконденсатных и нефтяных месторождений. Рассчитать молекулярную массу М_i каждого компонента, входящего в состав газа, молекулярную массу газа М_г, плотность газа при нормальных (_г^н.у.) и стандартных условиях (_г^ст.у.), а также относительную плотность по воздуху _г (при нормальных и стандартных условиях). Определить тип газа (природный, попутный или газ газоконденсатного месторождения). Исходные данные для расчетов приведены в таблицах 2.1 и 2.2.

Таблица 2.1 – Компонентный состав газа

Вариант	Месторождение	Компонентный состав газа, % объёмные
		СН4	С2Н6	С3Н8	С4Н10	С5Н12 и выше	СО2	N2	H2S
1	2	3	4	5	6	7	8	9	10
1	Самотлорское	53,40	7,20	15,1	8,30	6,30	0,10	9,60	-
2	Уренгойское (сеноман)	98,84	0,10	0,03	0,02	0,01	0,30	1,70	-
3	Оренбургское	84,00	5,00	1,60	0,70	1,80	1,10	4,20	1,60
4	Шатлыкское	95,60	2,00	0,34	0,10	0,05	1,15	0,76	-
5	Астраханское	58,80	1,88	0,60	0,23	0,12	11,0	1,37	26,0
6	Ромашкинское	37,30	20,70	18,9	9,50	4,80	-	8,80	-
7	Туймазинское	39,47	16,83	6,58	2,80	1,10	-	31,62	1,60
8	Южно-Первомайское	55,18	13,67	8,09	1,02	20,20	0,30	1,54	-
9	Бавлинское	35,00	20,70	19,9	9,80	5,80	0,40	8,40	-

Продолжение таблицы 2.1

1	2	3	4	5	6	7	8	9	10
10	ПО Пермьнефть	38,70	22,60	10,7	2,70	0,70	0,50	23,8	0,30
11	Коробковское	81,50	8,00	4,00	2,30	0,50	0,50	3,20	-
12	ПО Самаранефть	58,00	17,20	7,40	2,10	0,50	0,80	13,50	0,50
13	Ямбургское	89,67	4,39	1,64	0,74	2,36	0,94	0,26	-
14	ПО Грознефть	76,70	13,20	5,40	2,50	2,20	-	-	-
15	Медвежье	98,78	0,10	0,02	-	-	0,10	1,00	-
16	Вуктыльское	74,80	8,70	3,90	1,80	6,4	0,10	4,30	-
17	Тенгизское	42,23	8,47	5,21	3,34	21,18	2,60	0,77	16,2
18	Карачаганакское	72,99	6,22	2,59	1,50	7,55	5,35	0,57	3,23
19	Калужское	88,18	2,94	2,31	2,48	3,59	0,50	-	-
20	Узеньское	50,10	20,10	16,8	7,70	3,00	-	2,30	-
21	Талинское	44,88	7,38	3,85	1,39	42,50	-	-	-
22	Марковское	45,46	11,23	5,55	4,13	33,12	-	0,51	-
23	Уренгойское (валанжин)	82,27	6,56	3,24	1,49	5,62	0,50	0,32	-
24	Северо-Соленинское	89,52	4,15	1,82	0,48	2,58	0,49	0,96	-
25	Совхозное ПХГ	84,85	5,77	2,33	0,75	0,35	0,95	5,00	-
26	Дмитриевское	35,88	2,82	1,69	2,17	56,12	0,33	0,99	-
27	Северо-Ставропольское	92,80	2,80	0,90	0,40	0,10	0,50	2,50	-
28	Александровское	85,10	1,93	6,74	3,38	0,28	2,57	-	-
29	Радаевское	32,70	13,40	15,2	4,90	2,60	27,8	3,20	-
30	Ново-Дмитриевское	64,76	9,68	10,8	7,02	6,01	0,81	0,91	-

Таблица 2.2 – Атомные массы компонентов

Компонент	Водород	Углерод	Кислород	Сера	Азот
Атомная масса	1,008	12,011	15,999	32,064	14,007