
- •Теоретические основы электротехники
- •Часть 1
- •Введение
- •Условные графические обозначения элементов схем
- •Характеристики приборов, применяемых в эксперименте
- •Условные обозначения систем приборов
- •Лабораторная работа № 1
- •Результаты измерений и вычислений
- •Контрольные вопросы
- •Лабораторная работа № 2
- •Результаты исследования лэп постоянного тока
- •Лабораторная работа № 3
- •Исследование катушки индуктивности на постоянном токе
- •Измерение сопротивлений переменному току
- •Лабораторная работа № 4
- •Результаты измерений и вычислений
- •Лабораторная работа № 5
- •Результаты исследования резонанса напряжений
- •Лабораторная работа № 6
- •Результаты исследования резонанса токов
- •Лабораторная работа № 7
- •Результаты измерений и вычислений
- •Заключение
- •Библиографический список
- •Оглавление
- •Теоретические основы электротехники
- •Часть 1
- •6 80021, Г. Хабаровск, ул. Серышева, 47.
Исследование катушки индуктивности на постоянном токе
Вид измерения |
Измерено |
Вычислено |
|
U, В |
I, А |
R, Ом |
|
Без сердечника |
|
|
|
С сердечником |
|
|
|
Собрать схему (рис. 3.6) для определения сопротивлений на переменном токе. В качестве исследуемого элемента
 подключить:
подключить:
а) катушку без сердечника;
б) катушку с сердечником;
в) конденсатор без потерь;
г) конденсатор с потерями.
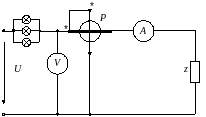
Рис. 3.6. Схема измерения сопротивлений на переменном токе
При измерении с помощью лампового реостата установить ток 1–2 А. Показания приборов и результаты вычислений записать в табл. 3.2.
Таблица 3.2
Измерение сопротивлений переменному току
Объект исследования |
Измерено |
Вычислено |
||||||||
U, В |
I, А |
P, Вт |
z, Ом |
R, Ом |
X, Ом |
φ, град |
L, Гн |
С, Ф |
||
|
|
|
|
|
|
|
|
|
|
|
Для всех исследуемых объектов построить векторные диаграммы напряжений и тока, треугольники сопротивлений.
Записать выводы по результатам исследований.
Контрольные вопросы
Объяснить изменение активного и реактивного сопротивления катушки при введении стального сердечника.
Вывести формулы для определения параметров
 параллельной схемы замещения элемента
в цепи синусоидального тока.
параллельной схемы замещения элемента
в цепи синусоидального тока.К последовательно соединенным
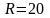 Ом и
Ом и
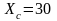 Ом приложено напряжение
Ом приложено напряжение
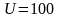 В. Найти величину тока в цепи и угол
сдвига фаз φ.
В. Найти величину тока в цепи и угол
сдвига фаз φ.По катушке с
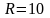 Ом и
Ом и
 мГн протекает ток
мГн протекает ток
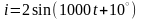 .
Определить мгновенное значение
напряжения на катушке.
.
Определить мгновенное значение
напряжения на катушке.Что такое «реактивное сопротивление» и как оно определяется?
Какая связь между полным, активным и реактивным сопротивлениями цепи переменного тока?
Как формулируется закон Ома для цепи переменного тока?
8. Может ли через конденсатор протекать постоянный ток?
9. Каковы углы сдвига фаз между напряжением и током на резисторе, реальной катушке и конденсаторе?
10. Какие
физические явления отражают в схеме
замещения конденсатора элементы
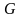 и
и
 ,
а в схеме замещения катушки индуктивности
элементы
и
?
,
а в схеме замещения катушки индуктивности
элементы
и
?
Лабораторная работа № 4
ИССЛЕДОВАНИЕ ПОСЛЕДОВАТЕЛЬНОЙ ЦЕПИ
СИНУСОИДАЛЬНОГО ТОКА С АКТИВНЫМ, ИНДУКТИВНЫМ
И ЕМКОСТНЫМ СОПРОТИВЛЕНИЯМИ
Цель работы: исследование режимов работы последовательной цепи синусоидального тока, определение параметров цепи, построение векторных диаграмм и треугольников сопротивлений.
Основные теоретические положения
Для цепи (рис. 4.1), состоящей из нескольких последовательно соединенных участков, напряжение на любом элементе можно определить по закону Ома
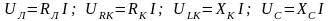 ,
,
где
– ток в цепи;
 – активные сопротивления ламп и катушки
индуктивности;
– активные сопротивления ламп и катушки
индуктивности;
 – индуктивное сопротивление катушки;
– индуктивное сопротивление катушки;
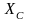 – емкостное сопротивление конденсатора.
– емкостное сопротивление конденсатора.

Рис. 4.1. Последовательная цепь переменного тока
Напряжение на входе цепи может быть определено из второго закона Кирхгофа в векторной форме как геометрическая сумма векторов напряжений на отдельных участках цепи.
В

Рис. 4.2. Векторная диаграмма последовательной цепи
екторная диаграмма напряжений для последовательной цепи построена так, что напряжения на активных сопротивлениях совпадают по фазе с током, на индуктивном – опережает на 90º, на емкостном – отстает от тока на 90º. Вектор напряжения – представляет сумму векторов
представляет сумму векторов
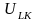 и
и
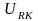 (рис. 4.2).
(рис. 4.2).
Величина напряжения на входе цепи находится из прямоугольного треугольника abc
 ,
,
где
 – активная составляющая напряжения;
– активная составляющая напряжения;
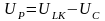 – реактивная составляющая напряжения.
– реактивная составляющая напряжения.
У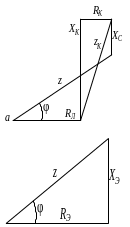 читывая
закон Ома для каждого элемента, получаем
закон Ома для всей цепи
читывая
закон Ома для каждого элемента, получаем
закон Ома для всей цепи
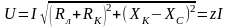 ,
,
где
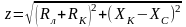 – полное сопротивление цепи.
– полное сопротивление цепи.
Разделив каждый вектор диаграммы на величину тока (рис. 4.2), получим подобный многоугольник, который называется многоугольник сопротивлений (рис. 4.3).
Для треугольника abc
(рис. 4.2) можно построить подобный
треугольник эквивалентных сопротивлений
всей цепи (рис. 4.4). Сопротивления
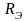 и
и
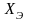 могут быть определены
могут быть определены

Угол φ определяет сдвиг фаз напряжения и тока на входе цепи. Его можно найти из выражения
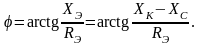
Изменяя
величины
и
,
можно добиться режима, при котором
 ,
хотя в цепи есть реактивные элементы.
,
хотя в цепи есть реактивные элементы.
Величина
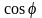 имеет важное технико-экономическое
значение, определяется по формуле
имеет важное технико-экономическое
значение, определяется по формуле
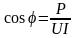
и называется коэффициентом мощности.
Порядок выполнения работы
Ознакомиться с оборудованием и приборами, записать их технические характеристики.
Собрать рабочую схему (рис. 4.1).
Включить питание и, изменяя сопротивление катушки и конденсатора, произвести измерения для трех режимов работы цепи: а) >>
 ;
б)
<<
;
в)
≈
.
;
б)
<<
;
в)
≈
.
4. Результаты измерений и вычислений занести в табл. 4.1.
Таблица 4.1
