Результаты исследования лэп постоянного тока

№ опыта	Измерено			Вычислено
	, В	, В	, А		, Вт	, Вт	, Вт	, В	, Ом	, Ом
1 2 3 …
1 2 3 …

4. Вычислить мощность в начале и в конце линии, потерю мощности и напряжения, сопротивление нагрузки и проводов линии, её кпд. Результаты расчётов свести в табл. 2.1.

5. Повторить эксперимент и расчет по пунктам 3 и 4 для повышенного напряжения в линии.

6. Построить совместно графики зависимостей , , _, , и отдельно для низкого и высокого напряжений в одинаковых масштабах.

7. Определить по графикам и таблицам отношения , , и кпд для режима, когда мощность в нагрузке принимает максимальное значение.

8. Записать выводы по результатам исследований.

Контрольные вопросы

1. Доказать, что напряжение на выходе ЛЭП уменьшается с ростом тока нагрузки.

2. Как зависит напряжение на потребителе от сечения проводов ЛЭП?

3. Почему мощность в нагрузке равна нулю при холостом ходе и при коротком замыкании?

4. Как зависят потери мощности от сопротивления ЛЭП?

5. Как подобрать сопротивление нагрузки, чтобы в ней выделялась максимальная мощность?

6. Чему равен кпд ЛЭП при максимальной мощности в нагрузке?

7. Может ли ток в ЛЭП превышать величину тока короткого замыкания?

8. Докажите, почему выгоднее эксплуатировать ЛЭП при высоком напряжении?

Лабораторная работа № 3

ИССЛЕДОВАНИЕ АКТИВНЫХ И РЕАКТИВНЫХ СОПРОТИВЛЕНИЙ

В ЦЕПИ ПЕРЕМЕННОГО СИНУСОИДАЛЬНОГО ТОКА

Цель работы: исследование свойств электрических цепей переменного тока; определение активных, реактивных и полных сопротивлений; исследование зависимости сопротивления катушки от рода тока и наличия сердечника; построение векторных диаграмм тока и напряжений, треугольников сопротивлений.

Основные теоретические положения

В электрических цепях переменного тока необратимое преобразование электрической энергии в другие виды энергии (тепловая, механическая) характеризуется активным сопротивлением участка цепи:

где – активная мощность, развиваемая переменным током на участке цепи; – действующее (среднеквадратичное) значение переменного тока.

В любом элементе цепи переменного тока происходит поглощение электрической энергии и выделение тепла, т. е. любой элемент обладает активным сопротивлением. Например, если катушка имеет сердечник из ферромагнитного материала, то, кроме потерь в проводах катушки, наблюдаются потери энергии в сердечнике на гистерезис и вихревые токи, что увеличивает активное сопротивление катушки.

В случае синусоидального тока напряжение на активном сопротивлении .

Н

Рис. 3.1. Векторная диаграмма для активного сопротивления

а активном сопротивлении фазы тока и напряжения совпадают (рис. 3.1).

При переменном токе связанное с ним маг­нитное поле изменяется во времени и на­водит эдс самоиндукции, величина кото­рой зависит от величины магнитного по­тока и скорости его изменения

.

Наиболее ярко выражено это явление в катушках индуктивности. По закону Ленца эдс самоиндукции препятствует изменению тока, т. е. оказывает сопротивление изменению тока, следовательно, катушка обладает сопротивлением переменному току. Введение ферромагнитного сердечника в катушку усиливает её магнитное поле, это приводит к увеличению эдс самоиндукции, следовательно, и сопротивления катушки.

В случае синусоидального тока явление самоиндукции учитывается индуктивным сопротивлением

где – угловая частота; – индуктивность элемента цепи.

Н

Рис. 3.2. Векторная диаграмма для индуктивного сопротивления

апряжение на индуктивном элементе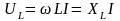 и опережает ток на 90° (рис. 3.2).

В электрические цепи могут входить также, элементы, обладающие электрической ёмкостью, т. е. способностью накапливать электрические заряды. Наиболее сильно это явление выражено в конденсаторах, представляющих собой две проводящих обкладки, разделенных слоем диэлектрика.

Если к конденсатору приложено постоянное напряжение, то заряды на обкладках постоянны и конденсатор представляет разрыв цепи.

В случае переменного напряжения происходит изменение заряда на обкладках, а, следовательно, в ветви с конденсатором протекает электрический ток.

Таким образом, емкостной элемент (конденсатор) для переменного тока обладает некоторым конечным сопротивлением. Для синусоидального тока емкостное сопротивление

,

где – ёмкость элемента.

Н

Рис. 3.3. Векторная диаграмма для емкостного сопротивления

апряжение на емкостном сопротивлении определяется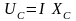 и отстает от тока на 90° (рис. 3.3).

В реальных конденсаторах активное сопротивление определяется потерями в диэлектрике. Для низких частот эти потери обычно невелики, поэтому с приемлемой точностью можно считать, что конденсатор обладает только емкостным сопротивлением.

В отличие от активного сопротивления , сопротивления и называют реактивными. Любой реальный элемент в цепи синусоидального тока можно представить в виде последовательного соединения активного и реактивного или сопротивлений. Схема замещения и векторная диаграмма тока и напряжений для катушки индуктивности приведена на рис. 3.4.

Рис. 3.4. Схема замещения (а); векторная диаграмма для катушки индуктивности и треугольник напряжений (б)

Величина напряжения на элементе определяется

где – полное сопротивление

Если стороны треугольника напряжений разделить на величину тока, то получим подобный треугольник, стороны которого равны полному , активному , реактивному сопротивлениям элементов цепи. Этот треугольник называют треугольником сопротивлений.

Угол φ (рис. 3.4) между векторами напряжения и тока называют углом сдвига фаз напряжения и тока. Его можно определить из треугольника напряжений или треугольника сопротивлений.

Разделение сопротивлений элементов цепей переменного тока на активное и реактивное является условным. Фактически нельзя выделить отдельно активное и реактивное сопротивление, например катушки. Они являются распределенными вдоль всей катушки и зависят, как было сказано выше, и от сердечника.

Порядок выполнения работы

1. Ознакомиться с оборудованием и приборами, записать их технические характеристики.

2. И

   

   Рис. 3.5. Схема измерения сопротивления на постоянном токе

   сследовать зависимость сопро­­тивления катушки (омического) по­сто­­янному току от наличия ферромаг­нит­ного сердечника. Схема измере­ний представления на рис. 3.5.

Величину тока установить в преде­лах 1–1,5 А с помощью лампового рео­стата. Измерить ток и напряжение на катушке без сердечника и при введенном стальном сердечнике. Резуль­таты измерений и вычислений занести в табл. 3.1.

Таблица 3.1