4.7. Квадратурные формулы интерполяционного типа

Для приближенного вычисления определенных интегралов часто используют следующий прием. Подынтегральную функцию аппроксимируют на функцией , интеграл от которой легко вычисляется и полагают Еще чаще используется другой подход. Интеграл представляют в виде суммы интегралов по отрезкам . На каждом таком отрезке аппроксимируют некоторой легко интегрируемой функцией и

Пусть - сетка на отрезке . Аппроксимируем на -м элементарном отрезке интерполяционным многочленом с узлами Например, можно воспользоваться многочленом Лагранжа Вычислим

Тогда . (4.7.1)

Формулы такого вида называются квадратурными формулами Ньютона - Котеса^.

4.8. Квадратурные формулы Гаусса

Итак, все квадратурные формулы имеют вид - веса. Формулы Гаусса строятся также по общему виду с дополнительным условием: формула должна быть точной для многочленов наиболее высокой степени. Как правило, формулы Гаусса сначала строятся для отрезка , то есть , а затем с помощью замены осуществляется переход к формулам интегрирования на произвольном отрезке:

Требование точности формулы для многочленов степени эквивалентно требованию ее точности для функции (базис для ). Следовательно,

(4.8.1)

Уравнение (4.8.1) дает систему нелинейных уравнений для определения Этих переменных штук. Следовательно, необходимый многочлен будет иметь степень , так как нужно учесть, что Построим, например, квадратурную формулу Гаусса с двумя и тремя узлами.

а). Индекс пробегает значения то есть - два узла. По формуле (4.8.1) получим

Итак, соответствующая нелинейная система уравнений имеет вид

Таким образом, получаем квадратурную формулу Гаусса:

(4.8.2)

точную для многочленов третьей степени.

б). Формула (4.8.1) дает

Аналогично для нахождения переменных будем иметь систему уравнений

Можно показать, что значения являются корнями многочленов Лежандра^ , а и так далее.

Итак, квадратурная формула Гаусса в случае б) имеет вид

(4.8.3)

Она точна до многочленов пятой степени. На таких же принципах могут быть построены квадратурные формулы Чебышева, Лагерра^, Эрмита.

Для квадратурной формулы Гаусса справедлива следующая оценка погрешности:

(4.8.4)

Ее коэффициенты убывают очень быстро, например,

4.9. Лабораторная работа № 8. Численное дифференцирование и численное интегрирование функций

Численное дифференцирование применяется в тех случаях, когда либо невозможно, либо очень сложно или дорого продифференцировать функцию аналитически. Из-за быстрого накопления ошибок при численном вычислении старших производных обычно ограничиваются нахождением первой и второй производной по формулам (4.1.1), (4.1.2) и (4.1.5).

Одним из способов повышения точности вычислений является уменьшение шага до предела, определяемого выражением (4.4.1). Однако если функция задана на сетке, то при численном дифференцировании невозможно выбрать шаг , меньший шага сетки, и тогда формулы (4.1.1)-(4.1.5) могут давать слишком большую погрешность. В этом случае исходную функцию часто аппроксимируют какой-либо гладкой функцией, значение производной от которой принимают за приближенное значение искомой производной.

Пример. Пусть дана функция Найдем ее первую и вторую производные, вычислим правую, левую и центральную первые разностные производные, вторую разностную производную по формуле (4.2.1) на отрезке и исследуем влияние шага на точность вычислений.

Легко проверить, что Выберем первоначально Введем с клавиатуры исходные данные и построим графики :

Первая и вторая производные этой функции уже найдены. Однако это можно было сделать в среде пакета Mathcad, причем двумя способами: с помощью панели инструментов Calculus (Панель операций математического анализа) и через меню символьных операций Symbolics.

С помощью меню производная находится следующим образом. В рабочий документ надо ввести выражение дифференцируемой функции, выделить синим уголком аргумент (переменную дифференцирования) и щелкнуть по строке Differentiate в пункте Variable меню Symbolics:

Ниже появится выражение для производной:

Выделяем все выражение и выбираем пункт Simplify в меню Symbolics. Ниже получим

В торая возможность связана с оператором символьных преобразований и оператором символьных преобразований с ключевым словом панели ключевых

с лов символьных выражений. Набираем оператор . В квадратик вставляем опера-тор из панели Calculus. После щелчка вне этого оператора слева от него появляется выражение для производной, которое можно упростить, выбрав оператор simplify в той же панели ключевых слов символьных выражений. В итоге получим следующее выражение:

Аналогичные действия нужно выполнить для нахождения второй производной, которая сразу получается в окончательном виде и более не упрощается оператором simplify.

Вводим с клавиатуры следующую информацию:

В точке возможно вычисление только правой разностной производной по формуле (4.1.1), в точке - только левой. Центральная разностная производная по формуле (4.1.5) не может быть посчитана при и . Вводим следующую часть программы:

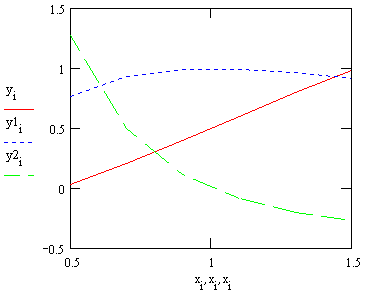
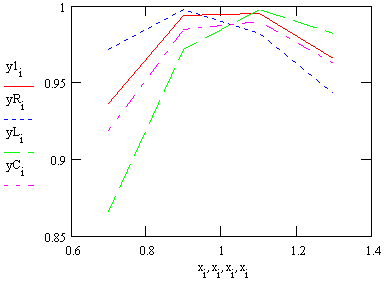
Наконец, находим вторую разностную производную по формуле (4.2.1). Она также не может быть посчитана в первой и последней точках заданной сетки узлов:

Уменьшим теперь шаг, например, в четыре раза. Для построения графиков необходимо пересчитать все значения функции и производных во всех новых точках сетки. Скопируем всю программу вместе с графиками после оператора Для этого надо, нажав левую мышку и не отпуская ее, обвести копируемую часть пунктирной линией. Затем щелкнуть по любому месту обведенной части правой мышкой. Появится дополнительное меню

Н еобходимо выбрать пункт копирования (Copy). Обведенная пунктирной линией часть программы скопируется в буфер обмена. Затем необходимо подвести курсор к нужному месту окна рабочего документа. Щелкнув в этом месте еще раз правой мышкой, раскроем то же дополнительное меню и выберем на этот раз пункт вставки (Paste). Копируемый кусок программы поместится ниже курсора. Приведем здесь лишь графики первых и вторых производных.

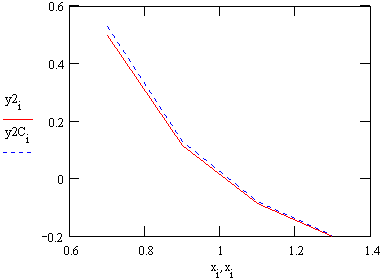
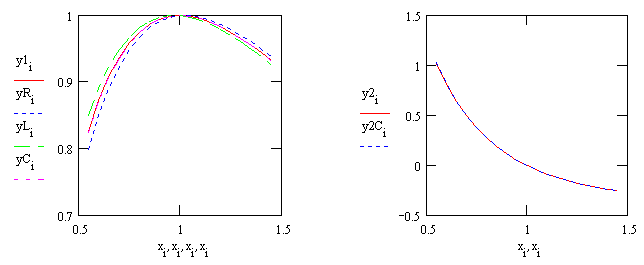
Видно, что точность представления производных заметно возросла. На первом графике первая центральная разностная производная, а на втором графике вторая разностная производная практически совпали с точными значениями, вычисленными по аналитическим выражениям:

Задание № 1. Для данных функций построить правую, левую и центральную первые разностные производные, вторую разностную производную на указанном интервале с данными шагами сетки и сравнить полученные значения с точными значениями производных:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

В среде Mathcad возможно численное интегрирование заданных функций и символьное интегрирование. Символьное интегрирование можно выполнить двумя способами, так же как и дифференцирование: с помощью панели операций математического анализа и через меню символьных операций.

С помощью меню нужно выполнить аналогичные действия, что и при дифференцировании: ввести выражение интегрируемой функции, выделить аргумент и щелкнуть по строке Integrate в пункте Variable меню Symbolics. В случае и получим

Таким образом, только интеграл от имеет действительное аналитическое выражение, выражается в комплексном виде. Аналогичный результат получается при использовании оператора символьных преобразований

Ч исленное интегрирование также можно осуществить двумя путями: с помощью панели операций математического анализа и панели равенств и отношений .

В среде Mathcad знак означает числовой, а знак символьный вывод значения переменной, функции или выражения, записанного до этого знака. При численном интегрировании удобнее пользоваться оператором . В нашем случае

Формулы численного интегрирования (4.5.3), (4.5.4) и (4.5.6) настолько просты, что значение интеграла можно подсчитать, используя несколько арифметических операторов или с помощью небольшой подпрограммы. Например, формула центральных прямоугольников реализуется таким образом:

П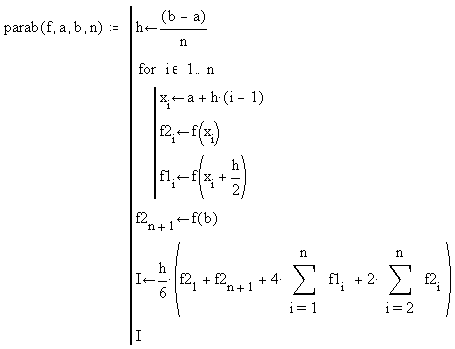 одпрограмма вычислений по формуле парабол (4.5.6) может быть такой:

Ее параметры: - интегрируемая функция, которая должна быть ранее определена в программе, - пределы интегрирования, - число точек сетки (четное число для формулы парабол).

Задание № 2. Найти численное значение интеграла от функций, указанных в задании № 1, на заданном промежутке. При вычислении по подпрограмме parab выбрать , соответствующее меньшему значению шага.

Содержание