2.9. Лабораторная работа № 2. Интерполирование и экстраполирование данных. Интерполяционный многочлен Лагранжа
В практических расчетах чаще всего используют интерполяционные многочлены невысоких степеней. Из формулы (2.3.4) видно, что единственный, восстанавливаемый без дополнительных условий многочлен Лагранжа должен иметь степень, на единицу меньшую числа точек интерполяционной таблицы. Обычно по исходным данным именно такой многочлен и восстанавливается. По найденному многочлену находят приближенные значения функции для любых значений аргумента, лежащих между узлами заданной сетки.
Пример. Найти многочлен наименьшей степени, принимающий в данных точках заданные значения:
-
0
1
2
1.45
1.36
1.14
3.14
4.15
5.65
Здесь
заданы лишь три узла сетки. Следовательно,
можно восстановить многочлен Лагранжа
второго порядка:
Вычислим вначале коэффициенты
Тогда
Для
вычисления лагранжевых коэффициентов
удобно применить следующую таблицу
разностей (2.9.1):
-
…
…
…
…
…
…
…
…
на главной диагонали которой стоят
разности вида
Если обозначить произведение элементов
-й
строки через
,
а произведение элементов главной
диагонали через
,
то
(2.9.2)
Для рассмотренного выше примера таблица разностей будет иметь вид
Тогда, например, для
получим
,
что совпадает с выражением, найденным
по формуле (2.3.4).
Теперь
по найденному интерполяционному
многочлену Лагранжа можно посчитать
приближенное значение функции
для любого значения аргумента
.
Вычислим, например,
Результат необходимо округлить до
второго знака после запятой. Итак,
Если
требуется найти не общее выражение
,
а лишь его значения при конкретных
значениях аргумента, то удобно пользоваться
интерполяционной схемой Эйткена по
формулам (2.8.1) и (2.8.2). Вычислим еще раз
,
расположив данные по схеме Эйткена в
удобной таблице (2.9.3):
-
0
1
2
Вычисления
по схеме Эйткена обычно ведут до тех
пор, пока последовательные значения
и
не совпадут в пределах заданной точности.
В нашем случае из-за малого количества узлов таблица получилась очень короткой, содержащей всего три многочлена: , и . Вычислим их:
-
0
1.45
3.14
0.035
1
1.36
4.15
-0.055
3.5328
2
1.14
5.65
-0.275
3.7750
3.5601
Итак,
Приведенный
пример показывает, что значение таблично
заданной функции в точке лучше вычислять
по схеме Эйткена, что обеспечивает
большую точность при меньших
вычислительных затратах. При определении
лагранжевых коэффициентов
возможна потеря точности из-за малых
знаменателей соответствующих дробей,
кроме того восстановленный
имеет большие и противоположные по
знаку коэффициенты, что также требует
сохранения лишних знаков в промежуточных
вычислениях.
Задание № 1. По образцу разобранного примера восстановить многочлен Лагранжа, удовлетворяющий приведенным исходным данным.
1.
-
0
1
2
3
0
1
2
5
2
3
12
147
2.
-
0
1
2
3
-2
1
2
4
25
-8
-15
-23
3.
-
0
1
2
3
4
-2
-1
0
1
2
6
0
2
0
6
4.
-
0
1
2
3
0
1
2
5
3
4
13
148
5.
-
0
1
2
3
-2
1
2
4
26
-7
-14
-22
6.
-
0
1
2
3
4
-2
-1
0
1
2
5
0
1
0
5
7.
-
0
1
2
3
-1
0
1
4
2
3
12
147
8
-
0
1
2
3
1
2
3
6
2
3
12
147
9.
-
0
1
2
3
-3
0
1
3
25
-8
-15
-23
10.
-
0
1
2
3
-1
2
3
5
25
-8
-15
-23
11.
-
0
1
2
3
4
-3
-2
-1
0
4
6
0
2
0
6
12.
-
0
1
2
3
4
-1
0
1
2
3
6
0
2
0
6
13.
-
0
1
2
3
2
3
4
7
2
3
12
147
14.
-
0
1
2
3
-2
-1
0
3
2
3
12
147
15.
-
0
1
2
3
-4
-1
0
2
25
-8
-15
-23
16.
-
0
1
2
3
0
3
4
6
25
-8
-15
-23
17.
-
0
1
2
3
-1
0
1
4
3
4
13
148
18.
-
0
1
2
3
1
2
4
6
1
2
34
146
19.
-
0
1
2
3
-3
0
1
3
26
-7
-14
-22
20.
-
0
1
2
3
-1
2
3
5
26
-7
-14
-22
21.
-
0
1
2
3
4
-3
-2
-1
0
1
7
1
3
1
7
22.
-
0
1
2
3
4
-1
0
1
2
3
5
-1
1
-1
5
23.
-
0
1
2
3
4
-1
0
1
2
3
2
1
0
1
10
24.
-
0
1
2
3
-2
-1
0
1
1
6
5
4
25.
-
0
1
2
3
-3
-2
-1
0
40
27
12
1
26.
-
0
1
2
3
4
-2
-1
0
1
2
-27
-4
-1
-6
-7
27.
-
0
1
2
3
-1
0
1
2
-5
-10
-1
34
28.
-
0
1
2
3
4
-2
-1
0
1
2
16
-1
0
1
8
29.
-
0
1
2
3
4
-2
-1
0
1
2
-23
-6
1
-2
9
30.
-
0
1
2
3
1
2
3
4
1
2
13
40
Задание № 2. Используя схему Эйткена,
вычислить приближенное значение функции
,
заданной таблично при данном значении
аргумента
.
I.
-
№ варианта
1
1.020
0.20
10.2316
6
1.140
0.80
10.9590
11
1.785
1.20
11.4725
16
2.031
1.70
12.1483
21
3.255
2.35
13.0120
26
3.512
3.00
14.0976
3.14
16.2134
3.61
19.0218
II.
-
№ варианта
2
0.616
0.45
2.5742
7
0.478
0.47
2.3251
12
0.665
0.52
2.0934
17
0.537
0.61
1.8620
22
0.749
0.66
1.7493
27
0.528
0.70
1.6210
0.74
1.3418
0.79
1.1212
III.
-
№ варианта
3
3.140
1.11
9.0542
8
2.351
1.59
6.6166
13
3.329
2.10
4.6917
18
2.756
2.96
3.3511
23
1.316
3.54
2.7995
28
5.555
4.00
2.3652
5.36
1.9418
5.78
1.8291
IV.
-
№ варианта
4
0.702
0.43
1.6360
9
0.512
0.48
1.7323
14
0.645
0.55
1.8769
19
0.736
0.62
2.0335
24
0.608
0.70
2.2285
29
0.762
0.75
2.3597
0.77
2.4103
0.83
2.6978
V.
-
№ варианта
5
8.960
6.81
8.0866
10
7.675
7.35
8.9492
15
9.490
8.00
10.2964
20
10.000
8.85
12.0966
25
8.125
9.34
13.4087
30
10.777
9.95
15.2368
10.25
18.1109
11.00
21.5445
В
ыполним
теперь те же действия в пакете Мathcad,
освоив простейшие символьные вычисления,
панель программирования, а также действия
с векторами и матрицами. Рассмотрим и
решим две задачи, аналогичные заданиям
№ 1 и № 2: построим многочлен Лагранжа
по заданной таблице и вычислим приближенное
значение функции по схеме Эйткена. Для
выполнения обеих этих задач удобно
воспользоваться аппаратом матричной
алгебры пакета.
К
нопка
-Vector and
Matrix Palette
(Панель векторных и матричных опе-раций)
открывает панель, изображенную чуть
ниже, кнопки которой соответствуют
следующим операциям:
-
определение размеров матрицы;
-
численное вычисление определителя
матрицы;
-
поэлементные операции с матрицами
(режим векторизации);
-
скалярное произведение двух векторов;
-
векторное произведение;
-
вычисление суммы компонент вектора
;
-
определение столбца матрицы:
-й
столбец матрицы;
-
транспонирование матрицы;
- визуализация цифровой информации, сохраненной в матрице.
Три действия: транспонирование, обращение матрицы и вычисление определите- ля - можно выполнить и из меню символьных операций (Symbolics).
Имеется три способа создания векторов и матриц в пакете Mathcad: заполнением массива пустых полей, предварительно созданной матрицы нужной размерности с помощью панели определения размеров; использованием дискретного аргумента, чтобы определить элементы матрицы; считыванием матрицы из файлов данных.
Итак, рассмотрим первую задачу. Пусть функция задана таблицей
-
-1
0
1
2
3
5
1
1
11
61
В ведем исходные данные и матрицу, соответствующую таблице (2.9.1). Для того чтобы определить вектор или матрицу, введем с клавиатуры имя вектора и знак присваивания. Затем щелкнем по кнопке и откроем окно диалога определения размеров матрицы:
П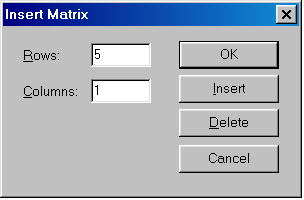
осле
этого заполним массив пустых полей,
получим на экране монитора
Переменная ORIGIN определяет начало нумерации строк и столбцов матрицы в пакете Mathcad, она описана в предыдущей лабораторной работе. Для определения таблицы (2.9.1) нужно задать функциональную, а не числовую матрицу, поэтому набираем
Д
алее
вычисляем лагранжевы коэффициенты по
формуле (2.9.2). Для этого необходимо
преобразовать символьное выражение.
Кнопка - Calculus Palette
(Панель операций математического
анализа) открывает панель, с помощью
которой можно суммировать, дифференцировать,
интегрировать, вычислять произведения
и находить пределы как числовых, так и
символьных выражений. Введем выражение
.
Щелчком по строке Simplify (Упростить) меню Symbolics (Символьные вычисления) символьному процессору передается выражение, выделенное в рабочем документе, а преобразованное выражение отображается в рабочем документе ниже или справа от исходного выражения в зависимости от задания стиля выражения (Evaluation Style).
В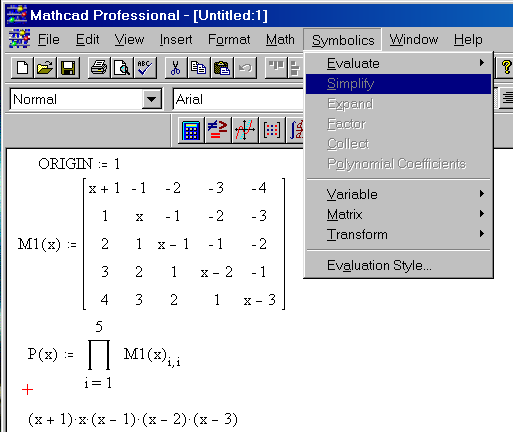
нашем случае получим на экране
Аналогично вычисляются знаменатели формулы (2.9.2):
Далее таким же образом вычисляем лагранжевы коэффициенты:
Наконец, получим сам многочлен Лагранжа:
По
найденной формуле можно приближенно
рассчитывать значения функции в любых
точках как внутри, так и вне табличного
интервала
с точностью, определяемой теоремой 2.2
(подразд. 2.4), например,
Решим
теперь задачу задания № 2. Пусть
задана таблицей и
-
0.05
0.10
0.17
0.25
0.30
0.36
0.43
0.49
0.0500
0.1003
0.1717
0.2553
0.3093
0.3767
0.4218
0.4536
П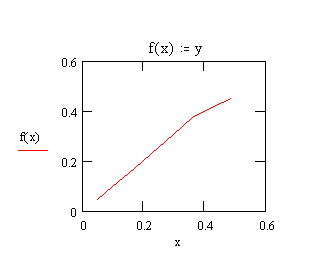
остроим
сначала, как
описано в
предыдущей
лабораторной
работе, график этой зависимости:
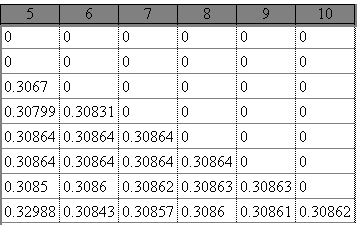
Далее последовательно строим числовую матрицу (2.9.3) схемы Эйткена при помощи дискретного аргумента:
Во всех приведенных таблицах задано пять знаков после запятой в данных, выводимых на дисплей. Это сделано таким образом. После двойного щелчка левой мыши открывается окно ввода параметров настройки отображения чисел, затем выставляется цифра 5 в верхнем окошке.
К сожалению, записать двойной цикл и вычислить все в одну строку с помощью дискретного аргумента здесь не удастся, так как, во-первых, нельзя в пакете Mathcad определять простую переменную через дискретный аргумент, во-вторых, переменные, определяющие дискретный диапазон, также не могут определяться через предыдущий дискретный аргумент. Однако эту задачу можно легко решить, составив коротенькую программу вычисления таблицы схемы Эйткена.
В
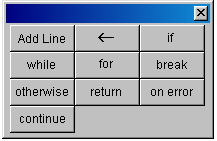оспользуемся
кнопкой -Programming Palette
(Панель программи-рования). Она открывает
следующую панель:
Кнопки этой панели вызывают операторы, во многом аналогичные основным операторам распространенных языков программирования. Язык Mathcad очень напоминает черты языка С. В этом нет ничего удивительного, так как сам Mathcad написан на этом языке. Основными составными операторами являются операторы выбора (if), повторения (until) и цикла (for) с заранее известным числом повторений. Кроме того, введено понятие локальной переменной, операторы досрочного выхода из цикла (break) и (continue) и оператор досрочного выхода из программы (return).
К
нопка
- это команда добавления строки в
программу или в тело цикла.
С
помощью этой кнопки алгоритмические
конструкции в программе или цикле могут
быть сделаны сколь угодно большими. При
нажатии этой кнопки в окне рабочего
документа появляется конструкция вида
. Вертикальная линия объединяет
отдельные
операторы
в
операторный блок с одним входом и одним
выходом, выполняющийся как единый
оператор. Кнопка -это оператор присваивания
значения локальной переменной.
К
нопка
вводит в программы альтернативу с одним
плечом
(
неполная
альтернатива). В первый квадратик (левее
if ) записывается
выполняемый оператор, в правый - булево
выражение. Выполняемый оператор
исполнится, если булево выражение
возвращает значение «Да» (в среде Mathcad
– любое числовое значение, отличное от
нуля). Для организации полной альтернативы
используется кнопка с оператором
otherwise . Кнопка
-это кнопка цикла с проверкой.
В
правый квадратик записывается булево
выражение, управляющее цик-
л
ом,
в нижний – тело цикла. Кнопка вводит в
программы цикл с параметром.
В
первый квадрат вводится переменная
цикла, в правом (после знака )
указываются пределы изменения этого
параметра. Эти пределы можно просто
перечислять через запятую или указывать
в том виде, как для дискретной переменной:
В нижний квадрат помещается тело цикла.
К
нопки
и позволяют досрочно выходить из
циклов while и for , а кнопка - из всей программы. При этом оператор break
передает управление обязательно в конец цикла, а оператор continue - в любое место цикла.
Н
аконец,
кнопка вводит оператор обработки ошибок.
Если при выполнении
о
ператора
в правом квадрате возникнет ошибка, то
будет выполняться оператор из левого
квадрата. Оператор on
error полезен в тех
случаях, когда ошибку сложно локализовать,
тем более что в программах пакета
Mathcad, к сожалению, невозможно
выводить на дисплей промежуточные
результаты расчета.
Итак, программа расчета матрицы схемы Эйткена может быть, например, такой:
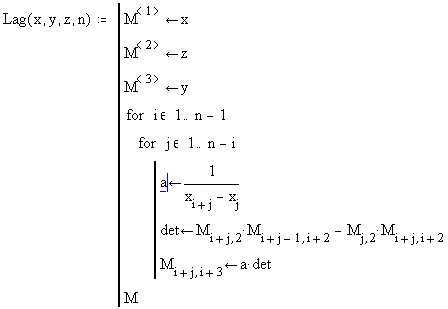
Параметрами
программы являются вектора исходных
данных
.
Компоненты вектора
равны:
,
-
число точек табличного задания функции
.
Для получения матрицы по схеме Эйткена
необходимо определить лишь вектор
и саму матрицу
:
